【转载】 推荐系统 EE 问题与 Bandit 算法

原文地址：

https://toutiao.io/posts/584etm/preview

-------------------------------------------------------------------------

生活中你可能会遇到类似的情况，你在网上购买了手机，淘宝之后会不断给你推送关于手机相关的商品；如果你看了关于NBA詹姆斯的相关新闻，今日头条之后会不断给你推送詹姆斯的新闻。时间长了，你会发现你的世界里只有手机和詹姆斯，天呐，世界越来越小，视野越来越窄怎么办？

别担心，上面的这种情况就属于EE问题的一种，更多的关于什么是推荐系统的EE问题可以参见：推荐系统EE（exploit－explore）问题概述。针对 EE 问题，可以使用 Bandit 算法来解决。这里介绍一些常用的 Bandit 算法。

Naive

Naive 的核心就在于朴素，它的做法就是先进行 N 次尝试，然后统计每个臂的平均收益，接下来一直选择平均收益最大的臂。这个算法是人们在实际中最常采用的。

Epsilon-Greedy（ε-Greedy）

Epsilon-Greedy 通过生成一个 (0,1) 范围内的数字 ε ，用它来表示概率，表示以 ε 的概率去从所有候选臂中随机选择一个，也就是 explore，以 1- ε 的概率去选择平均收益最大的臂，也就是 exploit。

通过 ε 的值可以控制对 explore 和 exploit 的权衡程度， ε 值越小，表明 explore 越保守，会有更好的稳定性。

很明显 ε 数值的确定是一件不容易的事情。

Thompson Sampling（汤普森采样）

介绍汤普森采样之前，可以先来介绍一个分布：beta 分布。beta 分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

beta 分布有两个控制参数：α 和 β 。先来看下几个 beta 分布的概率密度函数的图形：

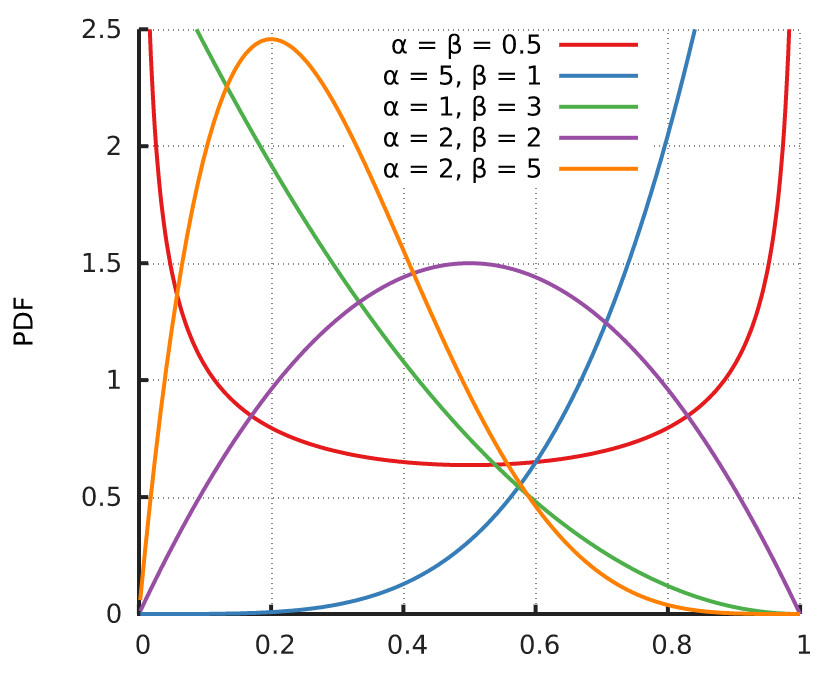
beta 分布图形中的 x 轴取值范围是 (0,1)，可以看成是概率值，参数 α 和 β 可以控制图形的形状和位置：

• α + β 的值越大，分布曲线越窄，也就是越集中。

• α/(α + β) 的值是 beta 分布的均值（期望值），它的值越大， beta 分布的中心越靠近 1，否则越靠近 0 。

注意：当参数 α 和 β 确定后，使用 beta 分布生成的随机数有可能不一样，所以汤普森采样法是不确定算法。

beta 分布和 Bandit 算法有什么关联呢？实际上，每个臂是否产生收益的概率 p 的背后都对应一个 beta 分布。我们将 beta 分布的 α 参数看成是推荐后用户的点击次数， β 参数看成是推荐后用户未点击的次数。

来看下使用汤普森算法的流程：

1. 每个臂都维护一个 beta 分布的参数，获取每个臂对应的参数 α 和 β，然后使用 beta 分布生成随机数。

2. 选取生成随机数最大的那个臂作为本次结果

3. 观察用户反馈，如果用户点击则将对应臂的 α 加 1，否则 β 加 1

在实际的推荐系统中，需要为每个用户保存一套参数，假设有 m 个用户， n 个臂（选项，可以是物品，可以是策略）， 每个臂包含 α 和 β 两个参数，所以最后保存的参数的总个数是 2 m n。

可以直观的理解下为什么汤普森采样算法有效：

• 当尝试的次数较多时，即每个臂的 α + β 的值都很大，这时候每个臂对应的 beta 分布都会很窄，也就是说，生成的随机数都非常接近中心位置，每个臂的收益基本确定了。

• 当尝试的次数较少时，即每个臂的 α + β 的值都很小，这时候每个臂对应的 beta 分布都会很宽，生成的随机数有可能会比较大，增加被选中的机会。

• 当一个臂的 α + β 的值很大，并且 α/(α + β) 的值也很大，那么这个臂对应的 beta 分布会很窄，并且中心位置接近 1 ，那么这个臂每次选择时都很占优势。

使用 python 来实现汤普森采样：

import  numpy as np

import  pymc

# wins 和 trials 都是一个 N 维向量，N 是臂的个数

# wins 表示所有臂的 α 参数，loses 表示所有臂的 β 参数

choice = np.argmax(pymc.rbeta(1 + wins, 1 + loses, len(wins)))

# wins[choice] += 1

# loses[choice] += 1

UCB（Upper Confidence Bound）

UCB 算法全称是 Upper Confidence Bound，即置信区间上界。它是计算每个臂的平均收益与该收益的不确定性来作为最终得分。公式如下：

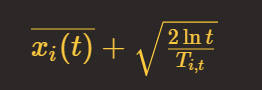
i 表示当前的臂，t 表示目前的尝试次数，Ti,t 表示臂 i 被选中的次数。公式加号左边表示臂 i 当前的平均收益，右边表示该收益的 Bonus ，本质上是均值的标准差，反应了候选臂效果的不确定性，就是置信区间的上边界。

使用 UCB 算法的流程如下：

1. 对所有臂先尝试一次

2. 按照公式计算每个臂的最终得分

3. 选择得分最高的臂作为本次结果

直观理解下 UCB 算法为什么有效？

• 当一个臂的平均收益较大时，也就是公式左边较大，在每次选择时占有优势

• 当一个臂被选中的次数较少时，即 Tit 较小，那么它的 Bonus 较大，在每次选择时占有优势

所以 UCB 算法倾向选择被选中次数较少以及平均收益较大的臂。

UCB 算法需要对所有的臂进行一次尝试，当臂比较多时，可能会比较耗时，如果 UCB 算法的参数是确定的，那么输出结果就是确定的，也就是说它本质上仍然是一个“确定性”的算法，这会导致它的 explore 能力受限。

总结

为解决推荐系统 EE 问题，可以使用 Bandit 算法，这里介绍了常用的 Bandit 算法，如：Naive、Epsilon-Greedy（ε-Greedy）、UCB（Upper Confidence Bound）等，但是这些算法都没有考虑上下文信息，也就是环境，之后会介绍结合上下文信息的 LinUCB 算法。