最近在学习TensorFlow,尝试的第一个项目是MNIST。首先给出源码地址。
1 数据集的获取
我们可以直接运行下面的代码,来获取到MNIST的数据集。
from tensorflow.examples.tutorials.mnist import input_data # 载入数据,并是labels进行one-hot编码 mnist = input_data.read_data_sets('./MNIST_data/',one_hot=True)
但是,由于网络的问题,input_data下载和解压数据时会出现问题,因此,我们只能手动下载MNIST的数据集。
这是下载地址,4个红色的连接即MNIST的数据集,下载下来,并放入MNIST_data文件中,然后运行上述代码就不会出错了。
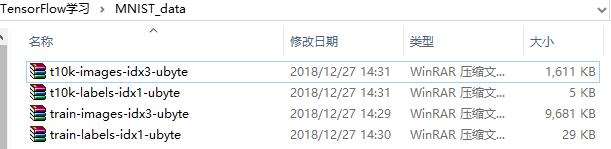
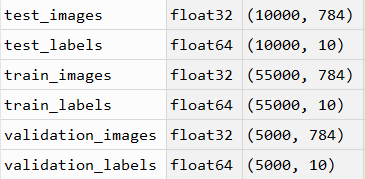
此时,文件有训练集、验证集和测试集,如下图所示。我们可以看到28*28的图像展开成了一维结果(28*28=784),丢弃了图像的空间结构,因为这是我们第一次尝试使用TensorFlow,不需要过于复杂。而标签值进行值one-hot编码。
# 下面是训练集、测试集和验证集的images和labels train_images = mnist.train.images train_labels = mnist.train.labels test_images = mnist.test.images test_labels = mnist.test.labels validation_images = mnist.validation.images validation_labels = mnist.validation.labels
2 MNIST分类学习
2.1 模型与原理
以训练集为例,我们知道训练集有55000个样本,并将每个样本展开成一维,因此X的大小为55000*784。而label经过one-hot编码,每一个样本的label对应一个1*10的向量,因此,label是55000*10的矩阵。
在这里,我们使用softmax regression来对图片进行分类。其中,softmax的表达式为
$$softmax(x_i)=frac{e^{x_i}}{sum_ {j} e^{x_j}}$$
此时,我们将分类出来的$y_i$进行概率归一化,选择概率最大的$y_i$作为其分类的结果。而怎么求$y_i$呢,我们可以定义一个模型,如下图所示,利用权重W和偏差b来表示:
$$y_i=softmax(x_{i}W+b)$$

当定义完我们的模型后,我们需要loss函数来就出最优的W和b。对于多分类问题,通常使用cross-entropy(交叉熵)来作为loss函数。交叉熵的定义为:
$$H(p,q)=-sum p(x)log(q(x))$$
其中,p为真实分布,q为预测分布。交叉熵越小,说明p和q的分布越接近。因此,我们对交叉熵使用梯度下降法,迭代更新W和b,最终得到最优解。
我们在下一个帖子详细介绍softmax+交叉熵的工作原理。
2.2 TensorFlow实现
首先,创建一个默认的session
# 创建一个新的session sess = tf.InteractiveSession()
然后,设置相关的x,W,b,y和y_,分别表示输入数据,权重,偏差,输出数据和真实标签值。
# x为images x = tf.placeholder(tf.float32,[None,784]) # W为权重 W = tf.Variable(tf.zeros([784,10])) # b为偏差 b = tf.Variable(tf.zeros([10])) y = tf.nn.softmax(tf.matmul(x,W)+b) y_ = tf.placeholder(tf.float32,[None,10])
其中,None表示不限条数的输入。对于训练集而言,x的大小为55000*784,每一行表示一个例子;W的大小为784*10,每一列代表第i列的权重;b的大小为1*10,在numpy中,如果矩阵与向量相加,其结果是矩阵中的每一行都与向量相加,因此要求矩阵的列数与向量的维数相等;y为计算出来的标签值,而y_则是真实的标签值,它们的大小都为55000*784。
对于多分类问题,通常使用cross-entropy(交叉熵)作为损失函数,利用梯度下降法来对其进行优化,此时就要使用到优化器。
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_*tf.log(y),reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
接下来,我们要初始化变量,并给其feed数据来进行迭代计算。
tf.global_variables_initializer().run() for i in range(1000): batch_xs,batch_ys = mnist.train.next_batch(100) train_step.run({x:batch_xs,y_:batch_ys})
最后,验证其准确度。在这里,argmax()函数是返回最大值的index,而其中的参数"1"表示轴1,即每一行,因此,返回的index即表示其分类出来的数字。通过tf.equal()来比较是否相同,最后,correct_prediction 会是一个列向量。
tf.cast()函数是将此数据类型转换成另外一种数据类型。为什么要转换,因为转换后可以计算平均值了。利用tf.reduce_mean()函数来求轴0的均值,当分类正确,其值为1,不正确,其值为0,因此计算出来的均值即准确度。
最后,我们需要对accuracy.eval()来查看其值,不能直接查看accuracy,因为查看不了。
correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32)) print(accuracy.eval({x:mnist.test.images,y_:mnist.test.labels}))
3、一些小技巧
- 当查看一个Variable时,通过将其赋予给一个变量,就可以查看里面的值。Variable在训练模型迭代中是持久化的。
y_value = y.eval({x:mnist.test.images,y_:mnist.test.labels})
b_value=b.eval()
如查看预测的y值,需要用eval()来进行查看。由于y的值需要feed,所以y.eval()需要feed参数。
如查看b的值,由于b是Variable,所以,直接另起等于变量即可查看。
上面代码的值可以在Spyder中查看。

reference:
[1] https://blog.csdn.net/cqrtxwd/article/details/79028264
[2] https://www.cnblogs.com/huliangwen/p/7455382.html
[3] 交叉熵:https://blog.csdn.net/tsyccnh/article/details/79163834
[4] 交叉熵:https://blog.csdn.net/mieleizhi0522/article/details/80200126