希尔排序（C语言）-解析

希尔排序

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。

---

　　希尔排序（Shell Sort）是将整个待排记录序列

（R₁,R₂,R₃,……,R_n）

　　按增量 d 划分为 d 个子序列，其中第 i (1 ≤ i ≤ d) 个子序列为

（R_i,R_i+d,R_i+2d,……,R_i+kd）

　　并分别对各个子序列进行直接插入排序；不断减少增量 d，重复这一过程；直到 d 减少到 1，对整个序列进行一次直接插入排序。增量 d 的取值序列

　　称为增量序列。基于增量序列的降序特点，希尔排序也被称为“缩小增量排序”。

---

 

　　希尔排序与直接插入排序的不同之处在于，直接插入排序每次对相邻记录进行比较，记录最多只移动了一个位置，而希尔排序每次对相隔较远距离

　　（即增量）的记录进行比较，使得记录移动时能跨过多个记录，实现宏观上的调整。当增量减小的 1 时，此时序列已基本有序，希尔排序的最后一趟

　　就是接近最好情况的直接插入排序。可将前面各趟的“宏观”调整看成是最后一趟的预处理，比如只做一次直接插入排序效率更高。

---

　假设待排序记录为10个，其对应的关键字序列为

（49　　38　　65　　97　　76　　13　　27　　49　　55　　04）

其中有两个49，后一个49加下划线以示区别。若增量序列为

（5 ，3  ,  1 ）

　　第一趟的增量 d₁ 为 5，将 10 个待排记录的分为 5 个子序列，如图所示，分别进行直接插入排序，结果为

（13　　27　　49　　55　　04　　49　　38　　65　　97　　76）。

PS：由于排序后加横线的49排到第一个49前面，因此希尔排序是不稳定的排序方法。

　　第二趟的增量 d₂ 为 3，将上一趟的结果分为 3 个子序列，如图所示，分别进行直接插入排序，结果为

（13　　04　　49　　38　　27　　49　　55　　65　　97　　76）。

（13　　04　　49　　38　　27　　49　　55　　65　　97　　76）。

　　第三趟的增量 d₃ 为 1，对整个序列进行直接插入排序，最后结果为

（04　　13　　27　　38　　49　　49　　55　　65　　76　　97）。

---

 

代码（C语言）：

#include<stdio.h>
#include<math.h>
 
#define MAXNUM 10
 
int main()
{
    void shellSort(int array[],int n,int t);//t为排序趟数
    int array[MAXNUM],i;
    printf("input 10 numberd :
");   //输入 
    for(i = 0;i < 10; i++)            //数组 
        scanf("%d",&array[i]);
    printf("
");
    shellSort(array,MAXNUM,int(log(MAXNUM+1)/log(2)));//排序趟数应为log2(n+1)的整数部分
    printf("the sorted numbers: 
");
    for(i = 0;i < 10; i++)            //输出数组 
        printf("%d ",array[i]);
    printf("
");
}
 
//根据当前增量进行插入排序
void shellInsert(int array[],int n,int dk)
{
    static int i,j,temp;
    for(i=dk;i<n;i++)//分别向每组的有序区域插入
    {
        temp=array[i];
        for(j=i-dk;(j>=i%dk)&&array[j]>temp;j-=dk)//比较与记录后移同时进行
            array[j+dk]=array[j];
        if(j!=i-dk)
            array[j+dk]=temp;//插入
    }
}
 
//计算Hibbard增量
int dkHibbard(int t,int k)
{
    return int(pow(2,t-k+1)-1);
}
 
//希尔排序
void shellSort(int array[],int n,int t)
{
    void shellInsert(int array[],int n,int dk);
    int i;
    for(i=1;i<=t;i++)
        shellInsert(array,n,dkHibbard(t,i));
}
 
//此写法便于理解，实际应用时应将上述三个函数写成一个函数。

输入/输出:

 

 

---

 

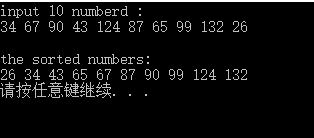
　　希尔排序的时间复杂度是所取增量序列的函数，尚难准确分析。有文献指出，当增量序列为 d[k] = 2^t-k+1-1 时，希尔排序的时间复杂度为 O(n^1.5),其中 t 为排序趟数， 1 ≤ k ≤ t ≤ [log₂(n+1)]。