2020软件工程作业04

| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/zswxy/2018SE |
| ---- | ---- | ---- |
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/zswxy/2018SE/homework/11406 |
| 这个作业的目标 | 寻找数组中第K大是哪个数 二叉树的先、中、后 序遍历与层级遍历 |
| 学号 | 20189611 |
| 其他参考文献 | https://www.bilibili.com/video/BV1os41117Fs?p=47|
题目名称：寻找数组中第K大是数 考察算法：排序算法
解题思路：先进行判断是否是满足条件小于10的六次方，然后建立数组存储输入的序列内容，进行循环输入l,r,k,循环次数为输入的m,
然后在建立一个数组存储截取到的第k个数进行判断k<=(r-l+1)调用数组的方法截取l到r的数值，存入新数组，然后调用数组sort
方法将其排序，新建一个答案数组存入，遍历数组输出。
解题代码：

        Scanner  input =new Scanner(System.in);
	 int n=0;
	do {
		System.out.print("请输入小于10的六次方的序列长度：");
		n =input.nextInt();
	} while (n>Math.pow(10, 6)&&n<1);` 
	//定义队列数组	
	 int [] line = new int[n];` 
	System.out.print("请输入序列值：");
	for (int i = 0; i < n; i++) {
		line[i]=input.nextInt();       	   
	}   
	System.out.print("请输入询问次数：");
	int m =input.nextInt();
	int l,r,k;
	//定义数组存储答案
	int []answer =new int[m];` 
	for (int j = 0; j < m; j++) {
		System.out.print("请输入l r k:");
		l =input.nextInt();
		r=input.nextInt();
		k=input.nextInt();
		if(k<=(r-l+1)){
			//Arrays.copyOfRange截取数组中下标l到r的数值，不包括r
			int[] newline =Arrays.copyOfRange(line, l-1, r);			
                           //for (int i = 0; i < newline.length-1; i++) {
                          //for (int o = 0; o < newline.length-1-i; o++) {
                          //if (newline[o]>newline[o+1]) {
                          //int temp =newline[o];
                          //newline[o]=newline[o+1];
                          //newline[o+1]=temp;
                           //}
                          //}
                        //	}			}

			//数组排序方法
			Arrays.sort(newline);
			answer[j]=newline[newline.length-k];
		}else {
			j--;
		}
	}
	System.out.println("输出:");
	for (int i : answer) {
		System.out.println(i);
	}

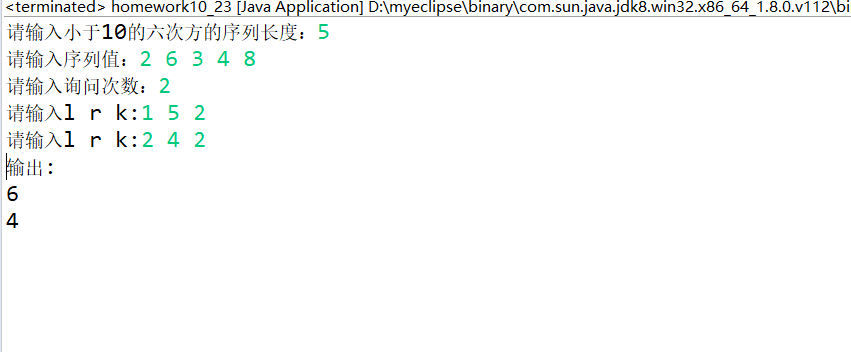
题目名称 二叉树的先、中、后 序遍历与层级遍历 考察算法
解题思路 前序遍历：先访问根节点然后遍历左子树，在前序遍历右子树 在题中是先打印根结点A也就是data数据,然后去调用前序遍历
方法只输入左孩子参数输出tdnb,然后调用前序遍历方法只输入右孩子参数输出49156

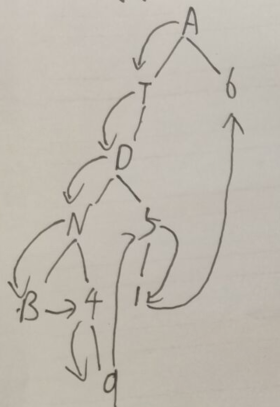
中序遍历 ：从最末端左子树开始，访问它的根结点，然后中序遍历右子树，一层层往上直至全部访问完成，所以先是调用左孩
子，然后是根结点，然后是右子树所以bn49然后一层层往上

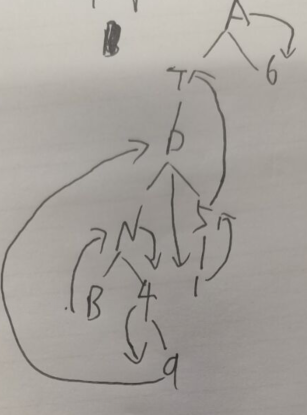
后序遍历：从左到右叶子优先，然后访问结点的方式所以是b94n 15d t6a

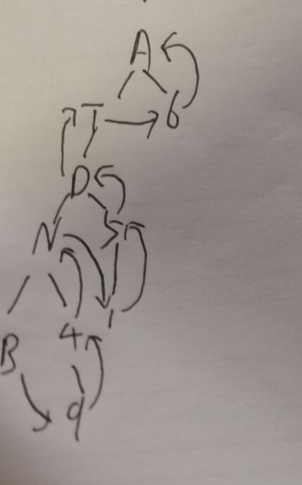
层级遍历就是从上往下从左到右，存入链表，先进后出

public class homewor1023_2 {
     public static void main(String[] args) {
	/*
        作业要求：叉树的先、中、后 序遍历与层级遍历
        自己实现四个方法，main方法中调用，将结果打印到控制台
	 */
	/*  二叉树的结构
                 A
                / 
               T   6
              /
             D
           /   
          N     5
         /     /
        B   4  1
             
              9
	 */

	Node root = into();
	// 先序遍历
	System.out.print("先序遍历：");
	A(root);
	System.out.println();
	// 中序遍历
	System.out.print("中序遍历：");

	B(root);
	System.out.println();

	// 后续遍历
	System.out.print("后续遍历：");
	C(root);
	System.out.println();

	// 层级遍历
	System.out.print("层级遍历：");
	D(root);
	System.out.println();

}

private static void A(Node node) {
	// TODO 先序遍历
	if (node != null) {
		System.out.print(node.data + " ");
		A(node.l);
		A(node.r);
	} 
}
private static void B(Node node) {
	// TODO 中序遍历
	if (node != null) {
		B(node.l);
		System.out.print(node.data + " ");
		B(node.r);
	}
}
private static void C(Node node) {
	// TODO 后续遍历
	if (node != null) {
		C(node.l);
		C(node.r);
		System.out.print(node.data + " ");
	}
}

private static void D(Node node) {
	// TODO 层级遍历
	if (node != null) {
		LinkedList<Node> List = new LinkedList<Node>();
		//先把根节点放到list
		List.add(node);
		Node newnode = null;
		while (!List.isEmpty()) {
			//移除列表中的一个元素(默认最后一个元素),并且返回该元素的值
			newnode = (Node) List.pop();
			System.out.print(node.data + " ");
			if (newnode.l != null) {			
				List.add(newnode.l);
			}
			if (newnode.r != null) {
				List.add(newnode.r);
			}
		}}
}

// 构建一颗树，返回根节点
private static Node into(){
	Node root = new Node("A");
	Node node1 = new Node("T");
	Node node2 = new Node("D");
	Node node3 = new Node("N");
	Node node4 = new Node("B");
	Node node5 = new Node("6");
	Node node6 = new Node("5");
	Node node7 = new Node("4");
	Node node8 = new Node("9");
	Node node9 = new Node("1");
	root.l = node1;
	node1.l = node2;
	node2.l = node3;
	node2.r = node6;
	node3.r = node7;
	node7.r = node8;
	node6.l = node9;
	node3.l = node4;
	root.r = node5;
	return root;
}

// 节点
static class Node{
	// 数据
	Object data;
	// 左孩子
	Node l;
	// 右孩子
	Node r;

	public Node(){}

	public Node(Object data) {
		this.data = data;
		this.l = null;
		this.r = null;
	}

	public Node(Object data, Node l, Node r) {
		this.data = data;
		this.l = l;
		this.r = r;
	}
}
   }