真题

 

1144. 递减元素使数组呈锯齿状

难度中等13收藏分享切换为英文关注反馈

给你一个整数数组 nums，每次 操作 会从中选择一个元素并 将该元素的值减少 1。

如果符合下列情况之一，则数组 A 就是 锯齿数组：

• 每个偶数索引对应的元素都大于相邻的元素，即 A[0] > A[1] < A[2] > A[3] < A[4] > ...
• 或者，每个奇数索引对应的元素都大于相邻的元素，即 A[0] < A[1] > A[2] < A[3] > A[4] < ...

返回将数组 nums 转换为锯齿数组所需的最小操作次数。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：我们可以把 2 递减到 0，或把 3 递减到 1。

示例 2：

输入：nums = [9,6,1,6,2]
输出：4

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= 1000

import copy 
class Solution:
    def movesToMakeZigzag(self, nums: List[int]) -> int:
        nums_len = len(nums)
        ans0 = 0
        ans1 = 0
        nums_copy0 = copy.deepcopy(nums)
        nums_copy1 = copy.deepcopy(nums)
        #奇数索引
        for index in range(nums_len):
            if index %2 == 1:
                d1 = d2 = 0
                if nums_copy1[index] <= nums_copy1[index-1]:
                    d1 = (nums_copy1[index-1] - (nums_copy1[index] - 1)) 
                    nums_copy1[index-1] = (nums_copy1[index] - 1)

                if (index+1< nums_len) and nums_copy1[index] <= nums_copy1[index+1]:
                    d2 = nums_copy1[index+1] - (nums_copy1[index] - 1)
                    nums_copy1[index+1] = (nums_copy1[index] - 1)

                ans1 += (d1+d2)

        #偶数索引
        for index in range(nums_len):
            if index %2 == 0:
                d1 = d2 = 0
                if index > 0 and nums_copy0[index] <= nums_copy0[index-1]:
                    d1 = (nums_copy0[index-1] - (nums_copy0[index] - 1)) 
                    nums_copy0[index-1] = (nums_copy0[index] - 1)

                if (index+1< nums_len) and nums_copy0[index] <= nums_copy0[index+1]:
                    d2 = nums_copy0[index+1] - (nums_copy0[index] - 1)
                    nums_copy0[index+1] = (nums_copy0[index] - 1)

                ans0 += (d1+d2)

        return min(ans0, ans1)

406. 根据身高重建队列

难度中等263收藏分享切换为英文关注反馈

假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对(h, k)表示，其中h是这个人的身高，k是排在这个人前面且身高大于或等于h的人数。 编写一个算法来重建这个队列。

注意：
总人数少于1100人。

示例

输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

class Solution:
    def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
        people.sort(key=lambda x:((-x[0],x[1])))
        res = list()
        for peo in people:
            res.insert(peo[1], peo)
        
        return res

582. 杀死进程

难度中等21收藏分享切换为英文关注反馈

给 n 个进程，每个进程都有一个独一无二的 PID （进程编号）和它的 PPID （父进程编号）。

每一个进程只有一个父进程，但是每个进程可能会有一个或者多个孩子进程。它们形成的关系就像一个树状结构。只有一个进程的 PPID 是 0 ，意味着这个进程没有父进程。所有的 PID 都会是唯一的正整数。

我们用两个序列来表示这些进程，第一个序列包含所有进程的 PID ，第二个序列包含所有进程对应的 PPID。

现在给定这两个序列和一个 PID 表示你要杀死的进程，函数返回一个 PID 序列，表示因为杀这个进程而导致的所有被杀掉的进程的编号。

当一个进程被杀掉的时候，它所有的孩子进程和后代进程都要被杀掉。

你可以以任意顺序排列返回的 PID 序列。

示例 1:

输入: 
pid =  [1, 3, 10, 5]
ppid = [3, 0, 5, 3]
kill = 5
输出: [5,10]
解释: 
           3
         /   
        1     5
             /
            10
杀掉进程 5 ，同时它的后代进程 10 也被杀掉。

注意:

1. 被杀掉的进程编号一定在 PID 序列中。
2. n >= 1.

class Solution:
    def killProcess(self, pid: List[int], ppid: List[int], kill: int) -> List[int]:
        graph = defaultdict(list)

        for p, pp in zip(pid, ppid):
            graph[pp].append(p)

        ans = []
        d = deque()
        d.append(kill)
        while d:
            cur = d.popleft()
            ans.append(cur)
            d.extend(graph[cur])

        return ans

56. 合并区间

难度中等324收藏分享切换为英文关注反馈

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

class Solution:
    def merge(self, intervals: List[List[int]]) -> List[List[int]]:

        intervals.sort(key=lambda x: x[0])

        merged = []
        for interval in intervals:
            # if the list of merged intervals is empty or if the current
            # interval does not overlap with the previous, simply append it.
            if not merged or merged[-1][1] < interval[0]:
                merged.append(interval)
            else:
            # otherwise, there is overlap, so we merge the current and previous
            # intervals.
                merged[-1][1] = max(merged[-1][1], interval[1])

        return merged

75. 颜色分类

难度中等367收藏分享切换为英文关注反馈

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]

进阶：

• 一个直观的解决方案是使用计数排序的两趟扫描算法。
  首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
• 你能想出一个仅使用常数空间的一趟扫描算法吗？

 

class Solution:
    def sortColors(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        if not nums:
            return 

        start = 0

        for index in range(len(nums)):
            if nums[index] == 0:
                nums[index] = nums[start]
                nums[start] = 0
                start += 1

        for index in range(len(nums)):
            if nums[index] == 1:
                nums[index] = nums[start]
                nums[start] = 1
                start += 1
        
        return 

820. 单词的压缩编码

难度中等46收藏分享切换为英文关注反馈

给定一个单词列表，我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。

例如，如果这个列表是 ["time", "me", "bell"]，我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。

对于每一个索引，我们可以通过从字符串 S 中索引的位置开始读取字符串，直到 "#" 结束，来恢复我们之前的单词列表。

那么成功对给定单词列表进行编码的最小字符串长度是多少呢？

示例：

输入: words = ["time", "me", "bell"]
输出: 10
说明: S = "time#bell#" ， indexes = [0, 2, 5] 。

提示：

1. 1 <= words.length <= 2000
2. 1 <= words[i].length <= 7
3. 每个单词都是小写字母 。

class Solution(object):
    def minimumLengthEncoding(self, words):
        good = set(words)
        for word in words:
            for k in range(1, len(word)):
                good.discard(word[k:])

        return sum(len(word) + 1 for word in good)

163. 缺失的区间

难度中等15收藏分享切换为英文关注反馈

给定一个排序的整数数组 nums ，其中元素的范围在 闭区间 [lower, upper] 当中，返回不包含在数组中的缺失区间。

示例：

输入: nums = [0, 1, 3, 50, 75], lower = 0 和 upper = 99,
输出: ["2", "4->49", "51->74", "76->99"]

class Solution:
    def findMissingRanges(self, nums: List[int], lower: int, upper: int) -> List[str]:

        res = []
        low = lower - 1
        nums.append(upper + 1)
        
        for num in nums:
            dif = num - low
            if dif == 2: 
                res.append(str(low+1))
            elif dif > 2: 
                res.append(str(low+1) + "->" + str(num-1))

            low = num

        return res

1162. 地图分析

难度中等27收藏分享切换为英文关注反馈

你现在手里有一份大小为 N x N 的『地图』（网格） grid，上面的每个『区域』（单元格）都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地，你知道距离陆地区域最远的海洋区域是是哪一个吗？请返回该海洋区域到离它最近的陆地区域的距离。

我们这里说的距离是『曼哈顿距离』（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

示例 1：

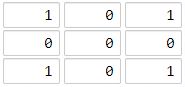
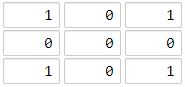
输入：[[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大，最大距离为 2。

示例 2：

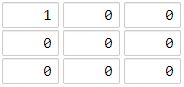
输入：[[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大，最大距离为 4。

from collections import deque
class Solution:
    def maxDistance(self, grid: List[List[int]]) -> int:
        # 地图规模
        n, m = len(grid), len(grid[0])
        # 每个点到陆地的曼哈顿距离
        dist = [[float('inf') for _ in range(m)] for _ in range(n)]
        # 该点是否被访问过
        visited = [[False for _ in range(m)] for _ in range(n)]
        # 队列
        q = deque()
        # 陆地计数
        cnt = 0
        ans = 0
        tot = n * m
        for i in range(n):
            for j in range(m):
                if grid[i][j]:
                    dist[i][j] = 0
                    visited[i][j] = True
                    q.append((i, j))
                    cnt += 1
        # 如果都是陆地或者都是海洋，则返回-1
        if cnt == tot or cnt == 0:
            return -1

        while q:
            x, y = q.popleft()# 出列
            for i, j in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]:
                # 如果坐标合法并且没被访问过
                if 0 <= i < n and 0 <= j < m and not visited[i][j]:
                    dist[i][j] = min(dist[i][j], dist[x][y] + 1) # 取最小值
                    ans = max(ans, dist[i][j]) # 更新答案
                    visited[i][j] = True
                    q.append((i, j)) # 入列
        return ans

957. N 天后的牢房

难度中等45收藏分享切换为英文关注反馈

8 间牢房排成一排，每间牢房不是有人住就是空着。

每天，无论牢房是被占用或空置，都会根据以下规则进行更改：

• 如果一间牢房的两个相邻的房间都被占用或都是空的，那么该牢房就会被占用。
• 否则，它就会被空置。

（请注意，由于监狱中的牢房排成一行，所以行中的第一个和最后一个房间无法有两个相邻的房间。）

我们用以下方式描述监狱的当前状态：如果第 i 间牢房被占用，则 cell[i]==1，否则 cell[i]==0。

根据监狱的初始状态，在 N 天后返回监狱的状况（和上述 N 种变化）。

示例 1：

输入：cells = [0,1,0,1,1,0,0,1], N = 7
输出：[0,0,1,1,0,0,0,0]
解释：
下表概述了监狱每天的状况：
Day 0: [0, 1, 0, 1, 1, 0, 0, 1]
Day 1: [0, 1, 1, 0, 0, 0, 0, 0]
Day 2: [0, 0, 0, 0, 1, 1, 1, 0]
Day 3: [0, 1, 1, 0, 0, 1, 0, 0]
Day 4: [0, 0, 0, 0, 0, 1, 0, 0]
Day 5: [0, 1, 1, 1, 0, 1, 0, 0]
Day 6: [0, 0, 1, 0, 1, 1, 0, 0]
Day 7: [0, 0, 1, 1, 0, 0, 0, 0]

示例 2：

输入：cells = [1,0,0,1,0,0,1,0], N = 1000000000
输出：[0,0,1,1,1,1,1,0]

提示：

1. cells.length == 8
2. cells[i] 的值为 0 或 1 
3. 1 <= N <= 10^9

class Solution:
    def prisonAfterNDays(self, cells: List[int], N: int) -> List[int]:

        def nextday(cells):
            return [int(i>0 and i< 7 and cells[i-1]==cells[i+1]) for i in range(8)]
        
        seen = {}
        while N > 0:
            cells_tuple = tuple(cells)
            if cells_tuple in seen:
                N %= (seen[cells_tuple] - N)

            seen[cells_tuple] = N 

            if N > 0:
                N -= 1
                cells = nextday(cells)
        
        return cells

1030. 距离顺序排列矩阵单元格

难度简单27收藏分享切换为英文关注反馈

给出 R 行 C 列的矩阵，其中的单元格的整数坐标为 (r, c)，满足 0 <= r < R 且 0 <= c < C。

另外，我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。

返回矩阵中的所有单元格的坐标，并按到 (r0, c0) 的距离从最小到最大的顺序排，其中，两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离，|r1 - r2| + |c1 - c2|。（你可以按任何满足此条件的顺序返回答案。）

示例 1：

输入：R = 1, C = 2, r0 = 0, c0 = 0
输出：[[0,0],[0,1]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1]

示例 2：

输入：R = 2, C = 2, r0 = 0, c0 = 1
输出：[[0,1],[0,0],[1,1],[1,0]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。

示例 3：

输入：R = 2, C = 3, r0 = 1, c0 = 2
输出：[[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
解释：从 (r0, c0) 到其他单元格的距离为：[0,1,1,2,2,3]
其他满足题目要求的答案也会被视为正确，例如 [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]]。

class Solution:
    def allCellsDistOrder(self, R, C, r0, c0):
        dist_list = [[] for i in range(200)]
        for i in range(R):
            for j in range(C):
                distinct = abs(r0-i) + abs(c0-j)
                dist_list[distinct].append([i, j])
 
        result = []
        for dist in dist_list:
            if dist:
                result.extend(dist)
            else:
                break
                
        return result