C. Ehab and Path-etic MEXs

output

standard output

You are given a tree consisting of nn nodes. You want to write some labels on the tree's edges such that the following conditions hold:

• Every label is an integer between 00 and n−2n−2 inclusive.
• All the written labels are distinct.
• The largest value among MEX(u,v)MEX(u,v) over all pairs of nodes (u,v)(u,v) is as small as possible.

Here, MEX(u,v)MEX(u,v) denotes the smallest non-negative integer that isn't written on any edge on the unique simple path from node uu to node vv.

Input

The first line contains the integer nn (2≤n≤1052≤n≤105) — the number of nodes in the tree.

Each of the next n−1n−1 lines contains two space-separated integers uu and vv (1≤u,v≤n1≤u,v≤n) that mean there's an edge between nodes uu and vv. It's guaranteed that the given graph is a tree.

Output

Output n−1n−1 integers. The ithith of them will be the number written on the ithith edge (in the input order).

Examples

input

Copy

3
1 2
1 3

output

Copy

0
1

input

Copy

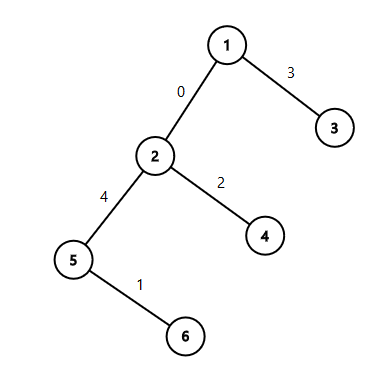
6
1 2
1 3
2 4
2 5
5 6

output

Copy

0
3
2
4
1

Note

The tree from the second sample:

#include <bits/stdc++.h>
#define ll              long long
#define PII             pair<int, int>
#define rep(i,a,b)      for(int  i=a;i<=b;i++)
#define dec(i,a,b)      for(int  i=a;i>=b;i--)
using namespace std;
int dir[4][2] = { { 0,1 } ,{ 0,-1 },{ 1,0 },{ -1,0 } };
const long long INF = 0x7f7f7f7f7f7f7f7f;
const int inf = 0x3f3f3f3f;
const double pi = 3.14159265358979323846;
const int mod = 998244353;
const int N = 1e5+5;
inline ll read()
{
    ll x = 0; bool f = true; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = false; c = getchar(); }
    while (c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
    return f ? x : -x;
}
ll gcd(ll m, ll n)
{
    return n == 0 ? m : gcd(n, m%n);
}
ll lcm(ll m, ll n)
{
    return m*n / gcd(m, n);
}

int main()
{
    ll n;
    cin >> n;
    vector<vector<int>> a(n + 1);
    vector<int> u(n+1),v(n+1);
    for (int i = 1; i<n ; i++) {
        cin >> u[i] >> v[i];
        a[u[i]].push_back(v[i]);
        a[v[i]].push_back(u[i]);
    }
    if (n == 2)
    {
        cout << 0 << endl;
        return 0;
    }
    int k=-1;
    rep(i,1,n)
    {
        if(a[i].size()>=3)
        {
            k=i;
            break;
        }
    }
    if(k==-1)
    {
        rep(i,0,n-2)
            cout<<i<<endl;
        return 0;
    }
    int tot=3;
    rep(i,1,n-1)
    {
        if(u[i]==k)
        {
            if(a[k][0]==v[i])
                cout<<0<<endl;
            else if(a[k][1]==v[i])
                cout<<1<<endl;
            else if(a[k][2]==v[i])
                cout<<2<<endl;
            else
                cout<<tot++<<endl;
        }
        else if(v[i]==k)
        {
            if(a[k][0]==u[i])
                cout<<0<<endl;
            else if(a[k][1]==u[i])
                cout<<1<<endl;
            else if(a[k][2]==u[i])
                cout<<2<<endl;
            else
                cout<<tot++<<endl;
        }
        else
            cout<<tot++<<endl;
    }
    return 0;
}