降维

主成分分析：

 

 

 

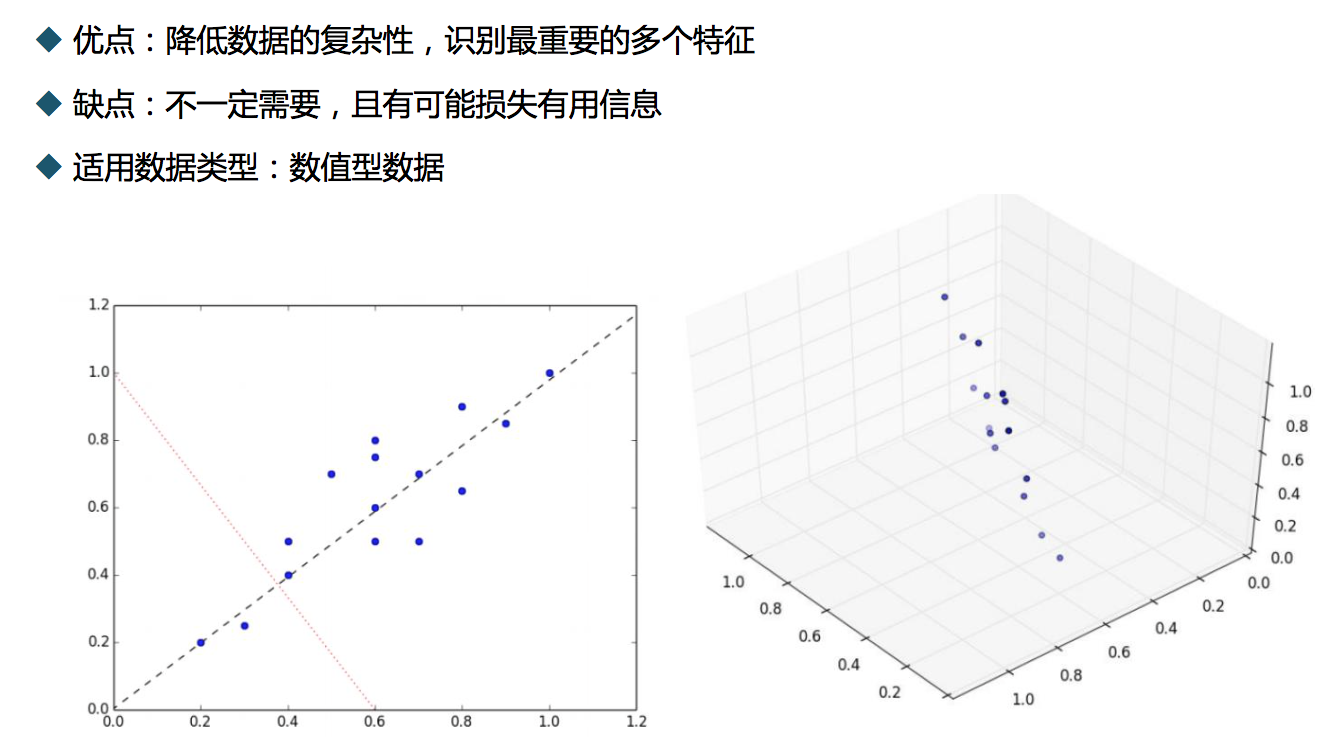
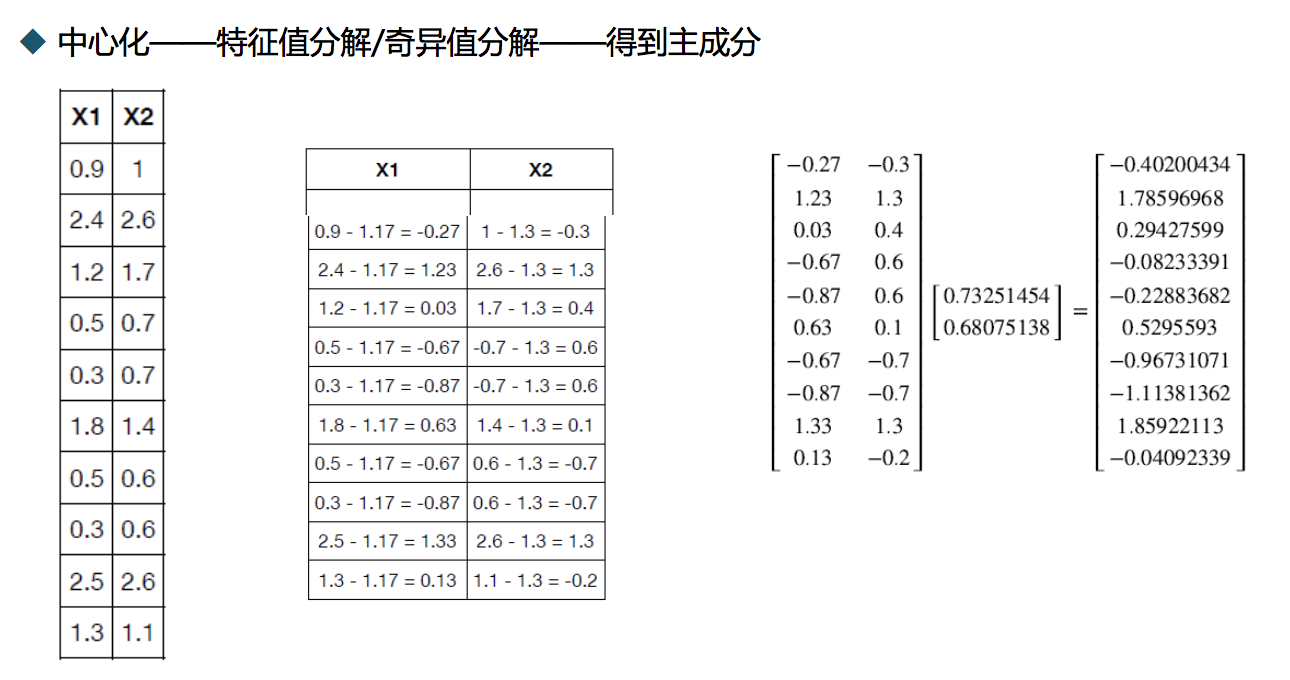
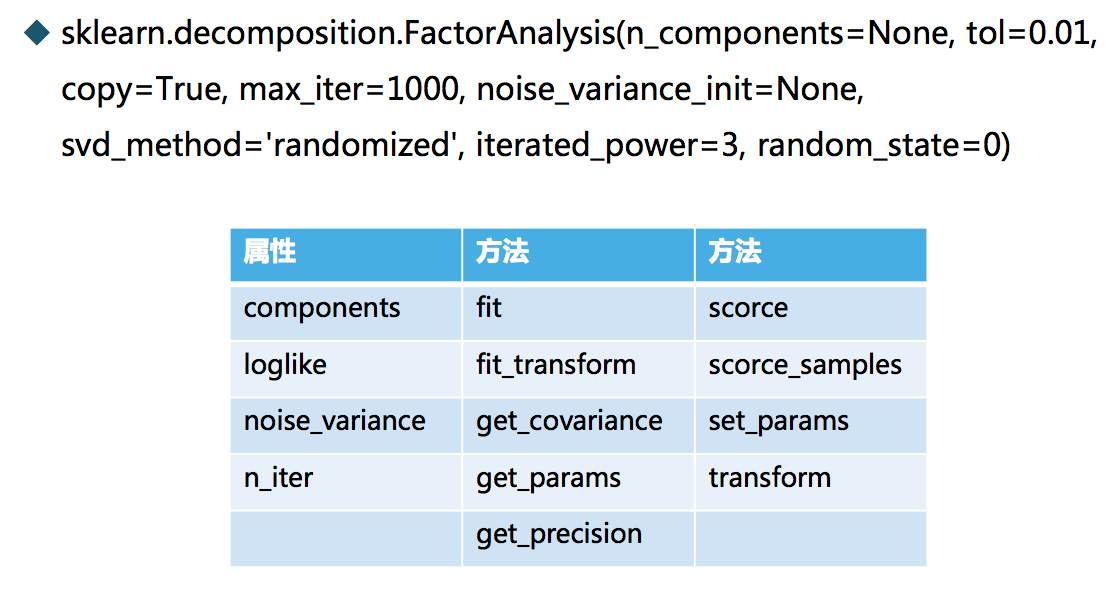
因子载荷矩阵和特殊方差矩阵的估计：

主成分法 ，主因子法 ，极大似然法 

---

#协方差矩阵
import numpy as np
X = [[2, 0, -1.4],
[2.2, 0.2, -1.5],
[2.4, 0.1, -1],
[1.9, 0, -1.2]]
print(np.cov(np.array(X).T))

#特征值与特征向量
w, v = np.linalg.eig(np.array([[1, -2], [2, -3]]))
print('特征值：{}
特征向量：{}'.format(w,v))


#鸢尾花数据集的降维
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data = load_iris()
y = data.target
X = data.data
pca = PCA(n_components=2)
reduced_X = pca.fit_transform(X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
for i in range(len(reduced_X)):
    if y[i] == 0:
        red_x.append(reduced_X[i][0])
        red_y.append(reduced_X[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_X[i][0])
        blue_y.append(reduced_X[i][1])
    else:
        green_x.append(reduced_X[i][0])
        green_y.append(reduced_X[i][1])
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')
plt.show()

---

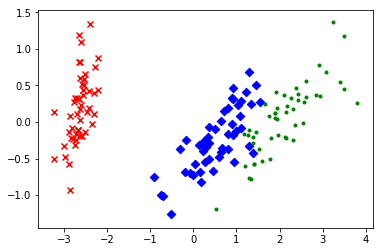
参考：炼数成金