写前面

*姐姐篇已完成 传送 canvas曲线面片2
(别跟我说这东西没用 并不想理你!)
什么是曲线面片? 如图


上面这个就是相对简单的双线性面片
可通过4个点来控制 左上角 A点 顺时针依次就是 ABCD
这个东西 其实就是 BA方向 和 DA 方向的线性插值组合 下图

先沿着DA CB 方向插值 再继续对 BA 方向插值
生成三角坐标的代码:
1 //初始点 2 var dot_ar = [ 3 new _$.Vec(0, 0) 4 ,new _$.Vec(w, 0) 5 ,new _$.Vec(w, h) 6 ,new _$.Vec(0, h) 7 ]; 8 9 //ABCD外围向量计算 10 var boundVec =()=>{ 11 V['BA'] = { 12 pv: dot_ar[0], 13 v: dot_ar[1].sub(dot_ar[0]) 14 }; 15 16 V['CB'] = { 17 pv: dot_ar[1], 18 v: dot_ar[2].sub(dot_ar[1]) 19 }; 20 21 V['CD'] = { 22 pv: dot_ar[3], 23 v: dot_ar[2].sub(dot_ar[3]) 24 }; 25 26 V['DA'] = { 27 pv: dot_ar[0] 28 , v: dot_ar[3].sub(dot_ar[0]) 29 }; 30 }; 31 //获取N个三角网络坐标 32 var getDots =cb=>{ 33 34 let k = +[]; 35 //DA CB 36 for (let i = 0; abs(i - 1) > .000001; i += hn) { 37 //++ 38 let s_da = V['DA'].v.scale(i + hn).add(V['DA'].pv); 39 let s_cb = V['CB'].v.scale(i + hn).add(V['CB'].pv); 40 41 42 let s_da_ = V['DA'].v.scale(i).add(V['DA'].pv); 43 let s_cb_ = V['CB'].v.scale(i).add(V['CB'].pv); 44 45 46 let vecx1 = { 47 48 v: s_cb_.sub(s_da_) 49 50 , pv: V['DA'].v.scale(i).add(V['DA'].pv) 51 }; 52 53 let vecx2 = { 54 v: s_cb.sub(s_da), 55 pv: V['DA'].v.scale(i + hn).add(V['DA'].pv) 56 }; 57 58 //再BA方向 59 for (let j = 0; abs(j - 1) > .000001; j += wn) { 60 // s_ba_ s_ba *vecx1 61 // s_ba2_ s_ba2 *vecx2 62 let s_ba = vecx1.v.scale(j + wn).add(vecx1.pv); 63 let s_ba2 = vecx2.v.scale(j + wn).add(vecx2.pv); 64 65 66 let s_ba_ = vecx1.v.scale(j).add(vecx1.pv); 67 let s_ba2_ = vecx2.v.scale(j).add(vecx2.pv); 68 69 //两个三角网络 70 cb && cb({ 71 0: { dot_ar: { 0: s_ba_, 1: s_ba, 2: s_ba2_ } }, 72 1: { dot_ar: { 0: s_ba2, 1: s_ba2_, 2: s_ba } } 73 }, k); 74 75 k += 2; 76 }; 77 }; 78 };
拿到坐标后就可以生成三角网络对象了
1 var createTrangle = ()=>{ 2 boundVec(); 3 //拿到坐标后 生成三角网络对象 4 getDots((dot,k)=>{ 5 trangle_ar.push( 6 TrangleMap({ 7 dot_ar: dot[0].dot_ar, 8 i: k, wireframe: prop.wireframe, 9 color: _$.color() 10 }) 11 ,TrangleMap({ 12 dot_ar: dot[1].dot_ar, 13 i: k + 1, wireframe: prop.wireframe, 14 color: _$.color() 15 }) 16 ); 17 }); 18 };
三角对象的代码:
1 var TrangleMap = prop=>{ 2 // setTransform 中の矩阵 3 var trans_ar = [ 4 1, 0, 0, 5 ,1, 0, 0 6 ]; 7 8 var dot_ar = prop.dot_ar; 9 10 //拷份初始点 11 var fix_dot = _$.extend([], dot_ar); 12 13 var color = prop.color || 'black'; 14 15 var draw = Object.create({ 16 line(){ 17 var ctx = Stg.ctx; 18 19 ctx.save(); 20 ctx.strokeStyle = color; 21 ctx.lineWidth = 2; 22 ctx.beginPath(); 23 ctx.moveTo(dot_ar[0].x, dot_ar[0].y); 24 ctx.lineTo(dot_ar[1].x, dot_ar[1].y); 25 ctx.lineTo(dot_ar[2].x, dot_ar[2].y); 26 27 ctx.closePath(); 28 29 ctx.stroke(); 30 ctx.restore(); 31 } 32 ,map(){ 33 var ctx = Stg.ctx; 34 35 ctx.save(); 36 //clip三角 37 ctx.beginPath(); 38 ctx.moveTo(dot_ar[0].x, dot_ar[0].y); 39 ctx.lineTo(dot_ar[1].x, dot_ar[1].y); 40 ctx.lineTo(dot_ar[2].x, dot_ar[2].y); 41 ctx.closePath(); 42 43 ctx.clip(); 44 45 ctx.save(); 46 47 ctx.setTransform.apply(ctx, trans_ar); 48 49 ctx.beginPath(); 50 ctx.drawImage(Pic.map, 0, 0, Pic.width, Pic.height); 51 ctx.closePath(); 52 ctx.restore(); 53 54 ctx.restore(); 55 } 56 }); 57 58 var _ = Object.create({ 59 render(){ 60 prop.wireframe && draw.line(); 61 draw.map(); 62 }, 63 transDot(){ 64 65 dot_ar = ar; 66 //X = ax + cy + 1e 67 //Y = bx + dy + 1f 68 69 var ar = [[fix_dot[0].x, fix_dot[0].y, 1], [fix_dot[1].x, fix_dot[1].y, 1], [fix_dot[2].x, fix_dot[2].y, 1]]; 70 71 //得到 a c e 72 var dtx = _$.Det3(ar, [dot_ar[0].x, dot_ar[1].x, dot_ar[2].x]); 73 //得到 b d f 74 var dty = _$.Det3(ar, [dot_ar[0].y, dot_ar[1].y, dot_ar[2].y]); 75 76 // a b c d e f 77 trans_ar = [dtx[0], dty[0], dtx[1], dty[1], dtx[2], dty[2]]; 78 } 79 }); 80 81 return _; 82 };
到这里确实已经可以形成面片了。。
但是 为何有个transDot方法 - -
因为我们还要对面片进行贴图操作 啊~
what? 贴图不是webgl 干的事么 。。 这里canvas2d也可以
一个三角对象就对应一个drawImage 如图:
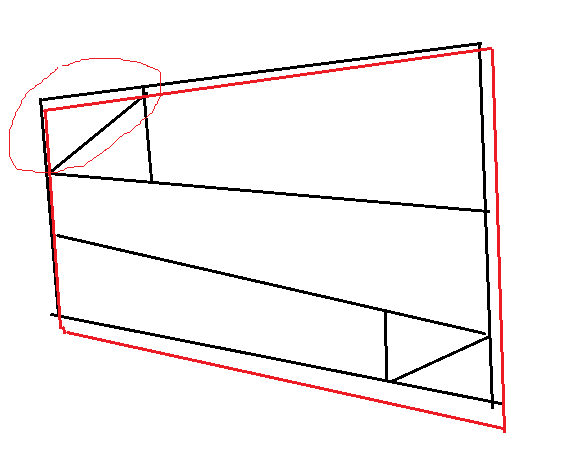
圈的那个三角贴图 是通过原始尺寸clip过的 但是clip又不帮你做拉伸缩放的变换。。
我们还得配合 transform 或者 setTransform api 传递矩阵参数
它内部是这样计算的
X = ax + cy + e
Y = bx + dy + f
我们要算出abcdef 也就是解个线性方程组
我用矩阵解法(也可用消元法) 我已经封装过了 那个Det3是这样的
1 Dai.Det3 = function(){ 2 var det = function(a){ 3 return a[0][0]*a[1][1]*a[2][2] 4 +a[0][1]*a[1][2]*a[2][0] 5 +a[0][2]*a[1][0]*a[2][1] 6 7 -a[0][2]*a[1][1]*a[2][0] 8 -a[0][1]*a[1][0]*a[2][2] 9 -a[0][0]*a[1][2]*a[2][1]; 10 }; 11 //x x x //Y 12 //x x x //Y 13 //x x x //Y 14 return function(ar,nar){ 15 var a,b,c; 16 var D = det(ar); 17 18 if(D==0) return console.warn('该矩阵不可逆~'); 19 20 var ar1 = _$.extend([],ar); 21 var ar2 = _$.extend([],ar); 22 var ar3 = _$.extend([],ar); 23 24 ar1[0][0] = nar[0]; 25 ar1[1][0] = nar[1]; 26 ar1[2][0] = nar[2]; 27 28 29 ar2[0][1] = nar[0]; 30 ar2[1][1] = nar[1]; 31 ar2[2][1] = nar[2]; 32 33 ar3[0][2] = nar[0]; 34 ar3[1][2] = nar[1]; 35 ar3[2][2] = nar[2]; 36 37 var D1 = det(ar1); 38 39 var D2 = det(ar2); 40 41 var D3 = det(ar3); 42 43 return [D1/D,D2/D,D3/D]; 44 } 45 }();
好了放出最终DEMO!