参考 信息熵是什么?
交叉熵损失函数原理详解
信息可以量化?
信息熵,信息熵,怎么看怎么觉得这个 “熵” 字不顺眼,那就先不看。我们起码知道这个概念跟信息有关系。而它又是个数学模型里面的概念,一般而言是可以量化的。所以,第一个问题来了:信息是不是可以量化?
起码直觉上而言是可以的,不然怎么可能我们觉得有些人说的废话特别多,“没什么信息量”,有些人一语中的,一句话就传达了很大的信息量。
为什么有的信息量大有的信息量小?
有些事情本来不是很确定,例如明天股票是涨还是跌。如果你告诉我明天 NBA 决赛开始了,这两者似乎没啥关系啊,所以你的信息对明天股票是涨是跌带来的信息量很少。但是假如 NBA 决赛一开始,大家都不关注股票了没人坐庄股票有 99% 的概率会跌,那你这句话信息量就很大,因为本来不确定的事情变得十分确定。
而有些事情本来就很确定了,例如太阳从东边升起,你再告诉我一百遍太阳从东边升起,你的话还是丝毫没有信息量的,因为这事情不能更确定了。
所以说信息量的大小跟事情不确定性的变化有关。
那么,不确定性的变化跟什么有关呢?
一,跟事情的可能结果的数量有关;二,跟概率有关。
先说一。
例如我们讨论太阳从哪升起。本来就只有一个结果,我们早就知道,那么无论谁传递任何信息都是没有信息量的。
当可能结果数量比较大时,我们得到的新信息才有潜力拥有大信息量。
二,单看可能结果数量不够,还要看初始的概率分布。例如一开始我就知道小明在电影院的有 15*15 个座位的 A 厅看电影。小明可以坐的位置有 225 个,可能结果数量算多了。可是假如我们一开始就知道小明坐在第一排的最左边的可能是 99%,坐其它位置的可能性微乎其微,那么在大多数情况下,你再告诉我小明的什么信息也没有多大用,因为我们几乎确定小明坐第一排的最左边了。
那么,怎么衡量不确定性的变化的大小呢?怎么定义呢?
这个问题不好回答,但是假设我们已经知道这个量已经存在了,不妨就叫做信息量,那么你觉得信息量起码该满足些什么特点呢?
一,起码不是个负数吧,不然说句话还偷走信息呢~
二,起码信息量和信息量之间可以相加吧!假如你告诉我的第一句话的信息量是 3,在第一句话的基础上又告诉我一句话,额外信息量是 4,那么两句话信息量加起来应该等于 7 吧!难道还能是 5 是 9?
三,刚刚已经提过,信息量跟概率有关系,但我们应该会觉得,信息量是连续依赖于概率的吧!就是说,某一个概率变化了 0.0000001,那么这个信息量不应该变化很大。
四,刚刚也提过,信息量大小跟可能结果数量有关。假如每一个可能的结果出现的概率一样,那么对于可能结果数量多的那个事件,新信息有更大的潜力具有更大的信息量,因为初始状态下不确定性更大。
那有什么函数能满足上面四个条件呢?负的对数函数,也就是 - log(x)!底数取大于 1 的数保证这个函数是非负的就行。前面再随便乘个正常数也行。
a. 为什么不是正的?因为假如是正的,由于 x 是小于等于 1 的数,log(x)就小于等于 0 了。第一个特点满足。
b. 咱们再来验证一下其他特点。三是最容易的。假如 x 是一个概率,那么 log(x)是连续依赖于 x 的。done
c。四呢?假如有 n 个可能结果,那么出现任意一个的概率是 1/n,而 - log(1/n) 是 n 的增函数,没问题。
d。最后验证二。由于 - log(xy) = -log(x) -log(y),所以也是对的。学数学的同学注意,这里的 y 可以是给定 x 的条件概率,当然也可以独立于 x。
By the way,这个函数是唯一的(除了还可以多乘上任意一个常数),有时间可以自己证明一下,或者查书。
ok,所以我们知道一个事件的信息量就是这个事件发生的概率的负对数。
信息量 I(X)= -log p(x)
最后终于能回到信息熵。信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。信息熵就是平均而言发生一个事件我们得到的信息量大小。所以数学上,信息熵其实是信息量的期望。
信息熵 
接下来就可以了解一下 通俗的解释交叉熵与相对熵
交叉熵损失函数
熵的本质是香浓信息量log(1/p) 的期望
既然熵的本质是香浓信息量log(1/p) 的期望,那么便有
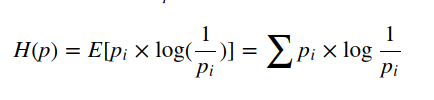
一个时间结果的出现概率越低,对其编码的 bit 的长度就越长。熵的本质的另一个解释是编码方案完美时,最短平均编码长度的是多少
在概率论或信息论中,KL 散度 (Kullback–Leibler divergence),又称相对熵(relative entropy),是描述两个概率分布 P 和 Q 差异的一种方法。它是非对称的,这意味着 D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q) 表示当用概率分布 Q 来拟合真实分布 P 时,产生的信息损耗,其中 P 表示真实分布,Q 表示 P 的拟合分布。简单的说,KL 散度或者相对熵它是用来度量两个分布P,Q 之间的距离的,也就是说,距离越大,两个分布差距最大。于是。在我们的模型训练中, 我们要做的就是不断的调整参数,使得预测得到的分布与真实分布尽可能的一致。那么,这与交叉熵有什么关系呢?
相对熵的数学定义如下

而H(pi) 是一个真实分布的期望,因此与训练无关,是一个常数项。于是,最小化相对熵便转为最小化 ![]()
这个就是交叉熵。
一句话说,就是,最小化误差可以通过最小化相对熵(KL 散度)来实现,而最小化相对熵,则可以通过最小化交叉熵来实现,所以,交叉熵损失函数就这么来了。。。。。。。。。