上一篇说到SVM需要求出一个最小的||w|| 以得到最大的几何间隔。
求一个最小的||w|| 我们通常使用

来代替||w||,我们去求解 ||w||2 的最小值。然后在这里我们还忽略了一个条件,那就是约束条件,在上一篇的公式(8)中的不等式就是n维空间中数据点的约束条件。只有在满足这个条件下,求解||w||2的最小值才是有意义的。思考一下,若没有约束条件,那么||w||2的最小值就是0,反应在图中就是H1和H2的距离无限大那么所有点都会在二者之间,都属于同一类,而无法分开了。
求最小值的目标函数和约束条件s.t.
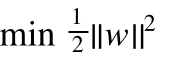
 (1)
(1)
xi和yi分别表示样本向量和样本所属的标签,w 是自变量,本身是一个向量。
求最小值也就是求最优值,它有一个很好听的名字叫做规划,而我们的目标函数是1/2 * ||w||2是一个二次函数,二次函数属于凸函数,所以改求解也就有个更好听的名字叫做凸二次规划
对于这种带有约束条件的规划问题,我们可以通过一定的方式把约束条件去掉!
凸函数和凸集
这里提一下凸函数,提到凸函数就要提交凸集或者凸包,凸集内的如意两个点的连线,都在凸集之内。满足这样的集合就叫凸集,比如正方形,六边形都是凸集。
那么凸函数:对区间[a,b]上定义的函数f,若它对区间中任意两点x1,x2均有:
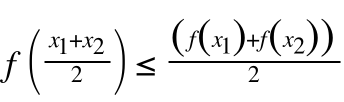 (2)
(2)则称f为区间[a,b]上的凸函数。
引入拉格朗日乘数,来消除约束条件
拉格朗日乘子法:
对于 带约束的优化问题:
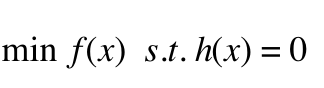 (3)
(3)
则可以通过拉格朗日乘子构造拉格朗日函数
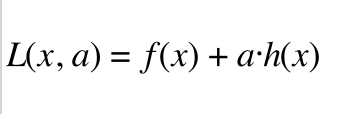 (4)
(4)
其中a是一个拉格朗日乘子构成的向量(a1,a2,a3,a4,....)ai>0
然后在对x 和 拉格朗日乘子a 求导,连立方程求出x 和 a ,再把x代入目标函数中求得极值.
回到我们的问题,通过拉格朗日乘子法构建拉格朗日函数, 在此之前我们把约束条件左边加上负号,让其条件变成小于0
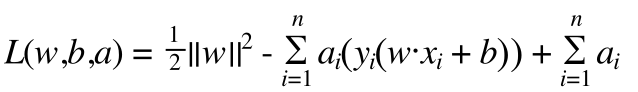 (5)
(5)
我们设
 (6)
(6)
如果xi满足约束条件,yi(w * xi + b) >= 1,则 θp(x)要取最大值,只能让 α= 0 就是取0向量,则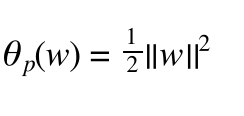 (7)
(7)
如果xi不满足条件 yi(w * xi + b) <= 1 要取最大值,那么α 可以无限大,所有
 (8)
(8)
所以我们看以看出 θp(x) 已经实现了把约束条件变成无约束条件
所以(1)中的带有约束条件的目标函数,就可以变成求(6)式(不带约束)的最小值,原因就是上面(7)和(8)公式 :
 (9)
(9)
我们直接求解此比较困难,需要这个式子转换成它的对偶问题(min 和 max 调换位置),再去求解这个对偶问题:
 (10)
(10)
为什么可以通过转换成对偶问题来求解原问题呢?因为存在这样一条定理设原问题的解为p* 它的对偶问题解为d*,一般情况下有d*<=p*, 证明过程就不写了。
所以求解对偶问题只能得到原问题解的下界,而不能保证d* = p*。
对这个对偶问题进行求解,先求minw,bL(w,b,a) 把a 当做常数 对w 和 b分别求导可以得到:
 (11)
(11)
 (12)
(12)
把(11)和(12)式代入 (5)式中可以求得minw,bL(w,b,a)
 (13)
(13)
可以看到(13)式中的w 和 b都消失了,(13)式是minw,bL(w,b,a)的值,求完最小值,还要求maxai>0
 (14)
(14)
如果把(14)问题中的 a 求出来,那么w 也就能求出来(通过(11)),b 也就可以求出了。
先不管怎么把a 求出来,因为这里有很多算法可以去求解,用的最多的就是SMO算法。
我们接下来证明这个通过对偶问题求出来的解 d* 就是我们想要的原问题解 p* ,这里就要介绍到KKT条件
根据(11)和 (12)式,我们可以得出

再根据原问题中的约束条件,我们可以得出

这5个条件加起来就满足了KKT条件,KKT条件是对偶问题的解d* = p* 的充分必要条件
以下是证明过程: