一、贝叶斯定理数学基础
我们都知道条件概率的数学公式形式为
 即B发生的条件下A发生的概率等于A和B同时发生的概率除以B发生的概率。
即B发生的条件下A发生的概率等于A和B同时发生的概率除以B发生的概率。
根据此公式变换,得到贝叶斯公式: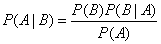 即贝叶斯定律是关于随机事件A和B的条件概率(或边缘概率)的一则定律。通常,事件A在事件B发生的条件溪的概率,与事件B在事件A的条件下的概率是不一样的,而贝叶斯定律就是描述二者之间的关系的。
即贝叶斯定律是关于随机事件A和B的条件概率(或边缘概率)的一则定律。通常,事件A在事件B发生的条件溪的概率,与事件B在事件A的条件下的概率是不一样的,而贝叶斯定律就是描述二者之间的关系的。
更进一步将贝叶斯公式进行推广,假设事件A发生的概率是由一系列的因素(A1,A2,A3,...An)决定的,则事件A的全概率公式为:
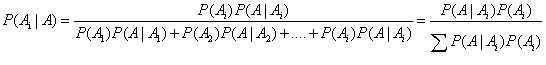
二、朴素贝叶斯分类
朴素贝叶斯分类是一种十分简单的分类算法,其思想基础是:对于给定的待分类项,求解在此项出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项就属于哪个类别。
假设V=(v1,v2,v3....vn)是一个待分项,而vn为V的每个特征向量;
B=(b1,b2,b3...bn)是一个分类集合,bn为每个具体的分类;
如果需要测试某个Vn归属于B集合中的哪个具体分类,则需要计算P(bn|V),即在V发生的条件下,归属于b1,b2,b3,....bn中哪个可能性最大。即:
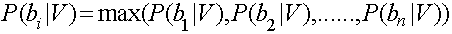
因此,这个问题转换成求每个待分项分配到集合中具体分类的概率是多少。而这个·具体概率的求法可以使用贝叶斯定律。
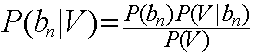
经过变换得出:
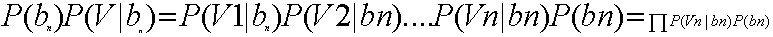
三、MLlib对应的API
1、贝叶斯分类伴生对象NativeBayes,原型:
object NaiveBayes extends scala.AnyRef with scala.Serializable {
def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
def train(input : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint], lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ }
}
其主要定义了训练贝叶斯分类模型的train方法,其中input为训练样本,lambda为平滑因子参数。
2、train方法,其是NativeBayes对象的静态方法,根据设置的朴素贝叶斯分类参数新建朴素贝叶斯分类类,并执行run方法进行训练。
3、朴素贝叶斯分类类NaiveBayes,原型:
class NaiveBayes private (private var lambda : scala.Double) extends scala.AnyRef with scala.Serializable with org.apache.spark.Logging { def this() = { /* compiled code */ } def setLambda(lambda : scala.Double) : org.apache.spark.mllib.classification.NaiveBayes = { /* compiled code */ } def run(data : org.apache.spark.rdd.RDD[org.apache.spark.mllib.regression.LabeledPoint]) : org.apache.spark.mllib.classification.NaiveBayesModel = { /* compiled code */ } }
4、run方法,该方法主要计算先验概率和条件概率。首先对所有样本数据进行聚合,以label为key,聚合同一个label的特征features,得到所有label的统计(label,features之和),然后根据label统计数据,再计算p(i),和theta(i)(j),最后,根据类别标签列表、类别先验概率、各类别下的每个特征的条件概率生成贝叶斯模型。
先验概率并取对数p(i)=log(p(yi))=log((i类别的次数+平滑因子)/(总次数+类别数*平滑因子)))
各个特征属性的条件概率,并取对数
theta(i)(j)=log(p(ai|yi))=log(sumTermFreqs(j)+平滑因子)-thetaLogDenom
其中,theta(i)(j)是类别i下特征j的概率,sumTermFreqs(j)是特征j出现的次数,thetaLogDenom一般分2种情况,如下:
1.多项式模型
thetaLogDenom=log(sumTermFreqs.values.sum+ numFeatures* lambda)
其中,sumTermFreqs.values.sum类别i的总数,numFeatures特征数量,lambda平滑因子
2.伯努利模型
thetaLogDenom=log(n+2.0*lambda)
5、aggregated:对所有样本进行聚合统计,统计没个类别下的每个特征值之和及次数。
6、pi表示各类别·的·先验概率取自然对数的值
7、theta表示各个特征在各个类别中的条件概率值
8、predict:根据模型的先验概率、条件概率,计算样本属于每个类别的概率,取最大项作为样本的类别
9、贝叶斯分类模型NaiveBayesModel包含参数:类别标签列表(labels)、类别先验概率(pi)、各个特征在各个类别中的条件概率(theta)。
四、使用示例
1、样本数据:
0,1 0 0 0,2 0 0 1,0 1 0 1,0 2 0 2,0 0 1 2,0 0 2
import org.apache.spark.mllib.classification.NaiveBayes import org.apache.spark.mllib.linalg.Vectors import org.apache.spark.mllib.util.MLUtils import org.apache.spark.{SparkConf, SparkContext} object Bayes { def main(args: Array[String]): Unit = { val conf=new SparkConf().setAppName("BayesDemo").setMaster("local") val sc=new SparkContext(conf) //读取样本数据,此处使用自带的处理数据方式· val data=MLUtils.loadLabeledPoints(sc,"d://bayes.txt") //训练贝叶斯模型 val model=NaiveBayes.train(data,1.0) //model.labels.foreach(println) //model.pi.foreach(println) val test=Vectors.dense(0,0,100) val res=model.predict(test) println(res)//输出结果为2.0 } }
import org.apache.log4j.{Level, Logger} import org.apache.spark.mllib.classification.NaiveBayes import org.apache.spark.mllib.linalg.Vectors import org.apache.spark.mllib.regression.LabeledPoint import org.apache.spark.{SparkConf, SparkContext} object Bayes { def main(args: Array[String]): Unit = { //创建spark对象 val conf=new SparkConf().setAppName("BayesDemo").setMaster("local") val sc=new SparkContext(conf) Logger.getRootLogger.setLevel(Level.WARN) //读取样本数据 val data=sc.textFile("d://bayes.txt")//读取数据 val demo=data.map{ line=>//处理数据 val parts=line.split(',')//分割数据· LabeledPoint(parts(0).toDouble,//标签数据转换 Vectors.dense(parts(1).split(' ').map(_.toDouble)))//向量数据转换 } //将样本数据分为训练样本和测试样本 val sp=demo.randomSplit(Array(0.6,0.4),seed = 11L)//对数据进行分配 val train=sp(0)//训练数据 val testing=sp(1)//测试数据 //建立贝叶斯分类模型,并进行训练 val model=NaiveBayes.train(train,lambda = 1.0) //对测试样本进行测试 val pre=testing.map(p=>(model.predict(p.features),p.label))//验证模型 val prin=pre.take(20) println("prediction"+" "+"label") for(i<- 0 to prin.length-1){ println(prin(i)._1+" "+prin(i)._2) }
val accuracy=1.0 *pre.filter(x=>x._1==x._2).count()//计算准确度
println(accuracy)
}
}