【前言】
背包问题是动态规划中的经典问题 ,特此总结三种背包问题的算法原理和一些基本实现,并且对每个问题提出了优化方案。目前只总结到初学者水平,以后拜读《背包九讲》之后如有新的体会再进行补充提升。欢迎读者批评指正。
【目录】
(1)0 - 1背包问题
(2)完全背包问题
(3)多重背包问题
【正文】
一、0 - 1背包
1.问题概述:有N种物品,每种物品只有一件,第i种物品的体积为c[i] , 价值为w[i] ,现有一个总体积为V的背包,求放入哪些物品能够使背包获得的体积最大。
2.问题分析:首先考虑贪心,一个容易想到的是如果我们按照 价值/体积 对物品进行排序,然后贪心地取前K种物品。但是这种策略对不对呢,显然是错误的。因为没有充分考虑到背包的容积特性,它是一个确切的数字,如果按照上述策略放物品,有可能使得背包还有大量未填充的空间。举个栗子,背包空间是8,物品有(3,3)(4,2)(3,3)(5,4),(x,y)代表价值为x,体积为y。怎么放呢?按照贪心,则先放(4,2) 再放(5,4),然后发现再也放不下了。这样得到的总价值是4+5 = 9,背包剩余空间是2。显然我们有一种更优的解决办法:放入(3,3)(4,2)(3,3),这样得到总价值为3+4+3 = 10,背包剩余空间是0.
因此我们需要用动态规划的眼光来解决这个问题,首先我们容易想到,如果先对前i件物品进行选择,dp[i][j]表示前i种物品装入体积为j的背包所能获得的最大值,那么我们最终的目的就是求dp[N][V]
状态转移方程:dp[i][j] = max{ dp[i-1][ j - c[i] ] + w[i] , dp[i-1][j] } 也就是说对于第i件物品我们要么选要么不选,取最终价值最大的那个。
注:这里的i 从 1~N j可以从0~V 也可以从V~0
3.【AC代码】正向 vs 逆向
HDU 2602 Bone Collector 模板题

#include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int n,v; int dp[maxn][maxn]; int main(){ int t; cin>>t; while(t--){ cin>>n>>v; memset(dp, 0 ,sizeof dp); for(int i=1; i<=n; i++){ cin>>w[i]; } for(int i=1; i<=n; i++){ cin>>c[i]; } //逆推,从背包空间为V开始 for(int i=1; i<=n; i++){ for(int j=v; j>=0; j--){ if(j >= c[i]) dp[i][j] = max( dp[i-1][j], dp[i-1][j-c[i]] + w[i]); else dp[i][j] = dp[i-1][j]; } } cout<<dp[n][v]<<endl; } }

#include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int n,v; int dp[maxn][maxn]; int main(){ int t; cin>>t; while(t--){ cin>>n>>v; memset(dp, 0 ,sizeof dp); for(int i=1; i<=n; i++){ cin>>w[i]; } for(int i=1; i<=n; i++){ cin>>c[i]; } for(int i=1; i<=n; i++){ //正向递推,背包体积从0开始到V for(int j=0; j<=v; j++){ if(j-c[i] >= 0) dp[i][j] = max( dp[i-1][j], dp[i-1][j-c[i]] + w[i]); else dp[i][j] = dp[i-1][j]; } } cout<<dp[n][v]<<endl; } }
4. 空间优化:我们可以注意到,如果把dp二维数组画成一个矩阵,那么求dp[i][j]的时候,我们其实只用到了它头顶上的一个元素dp[i-1][j],以及头顶上元素的左边某一个元素dp[i-1][j-c[i]],这两个元素都在dp[i][j]头顶上的那一行,逐渐往下递推的时候其实每次用的都是它头顶上的那一行,那么我们可不可以只用一维数组并且不断更新这个数组呢?答案是可以的,这个数组还有一个名字,叫滚动数组。也就是说我们用的数组始终保存的是“它头顶上的那一行”,不断覆盖。设dp[i]表示背包体积为i时最多能获得的价值,我们最终的目的是求的dp[N]。
需要注意的是,用滚动数组求dp[i][j]时会发生覆盖,那么什么时候才能覆盖那个元素呢,那就是那个元素已经没有用了,所以我才能覆盖它,那么它什么时候没有用了呢?首先我们考虑它的用处,它的用处是求它脚底下一行的元素,以及求它脚底下右边某处的元素,当这两个元素都已经被求出来的时候,它就没用了。按照这样的思想,我们只能从右往左倒着求dp[i],先把右边的元素求出来。
图解:
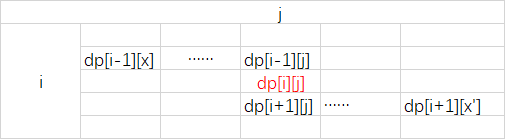
【空间优化后的代码】

#include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int n,v; int dp[maxn];//dp[i]表示背包体积为i时获得的最大价值 int main(){ int t; cin>>t; while(t--){ cin>>n>>v; memset(dp, 0 ,sizeof dp); //读入价值 for(int i=1; i<=n; i++){ cin>>w[i]; } //读入代价 for(int i=1; i<=n; i++){ cin>>c[i]; } for(int i=1; i<=n; i++){ for(int j=v; j>=c[i]; j--){ dp[j] = max(dp[j-c[i]] + w[i], dp[j]); } } cout<<dp[v]<<endl; } }
二、完全背包
1.问题概述:有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],价值是w[i]。求如何放置物品到背包中使得获得的价值最大,最大价值是多少。
2.问题分析: 完全背包问题和0-1背包问题的区别在0-1背包问题中所有物品只有一件,或者说只能取一次,而完全背包中所有种类的物品均可以取无限次,次数k的范围是 [0, V/c[i] ] 那么递推方程就转化为:
dp[i][j] = max( dp[i-1][j], dp[i-1][ j - k*c[i] ] + k*w[i] | 0=< k*c[i] <= j)
当然,k的范围是可求的所以也可以把它转化成0-1背包问题,那就是第种物品有Ki件,每件一毛一样,每件只能被取一次,多加一层K循环即可,但是这样一来复杂度相当高。
3.空间优化:那么能不能继续使用滚动数组呢?
回想一下,0-1背包问题为什么要逆序循环,因为在算下一次的 i 的 dp[j]时,必须先算右边的(即j大的)以解决覆盖问题。每次求dp[v]时,使用的是dp[v - c[i]],这是上一轮所算出来的,不是这一轮算出来的所以保证了每一轮算dp[v]时使用的都是上一轮的结果,也就保证了每件物品在每轮计算中都只被选一次。如果我们正序计算dp[v], 则算dp[v]时使用的dp[v - c[i]]是这一轮的,也就是第i件物品又被选了一次,它可以被选择多次。
其实也可以这样理解,在第一轮中,背包中放的都是第一种物品,放了0件,1,件,2件...... V/c[1]件的结果都知道;第二轮时,在第一轮的基础上,放入若干第二种物品,更新dp[i]使其暂时最优,一直放到最后一种,不断更新dp[i]使其最优。
【代码】

#include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int n,v; int dp[maxn];//dp[i]表示背包体积为i时获得的最大价值 int main(){ int t; cin>>t; while(t--){ cin>>n>>v; memset(dp, 0 ,sizeof dp); //读入价值 for(int i=1; i<=n; i++){ cin>>w[i]; } //读入代价 for(int i=1; i<=n; i++){ cin>>c[i]; } //正序递推 for(int i=1; i<=n; i++){ for(int j=c[i]; j<=v; j++){ dp[j] = max(dp[j-c[i]] + w[i], dp[j]); } } cout<<dp[v]<<endl; } }
三、多重背包
1.问题概述:有N种物品和一个体积为V的背包,第i种物品最多有n[i]件,花费为c[i], 价值为w[i], 问怎样放使得背包总价值最大?输出最大总价值。
2.问题分析: 多了一个限制条件,每种物品最多有n[i]件,其实不还是和完全背包一样,完全背包每件物品最多V/c[i]个,这里是给定的n[i]个。
dp[i][j] = max( dp[i-1][j], dp[i-1][ j - k*c[i] ] + k*w[i] | 0=< k*c[i] <= min(n[i] , V/c[i]))
或者这样说,把这n[i]件物品看做是n[i]种物品,每种物品只能取一次,这样不就和0-1背包一毛一样了吗?
3.例题:庆功宴 http://ybt.ssoier.cn:8088/problem_show.php?pid=1269
【AC代码】

#include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int s[maxn]; int n,v; int dp[6*maxn];//dp[i]表示背包体积为i时获得的最大价值 int main(){ //int t; //cin>>t; while(cin>>n>>v){ memset(dp, 0 ,sizeof dp); //读入价值 for(int i=1; i<=n; i++){ cin>>c[i]>>w[i]>>s[i]; } for(int i=1; i<=n; i++){ for(int j=v; j>=c[i]; j--){ for(int k=1; k<=s[i]; k++){ if(j >= k*c[i]){ dp[j] = max(dp[j-k*c[i]] + k*w[i], dp[j]); } else break; } } } cout<<dp[v]<<endl; } }
4.二进制优化
如果数据规模比较大,那么用K循环枚举物品被放入0个到n[i]个的情况时间复杂度比较高,可以采用二进制压缩的方法,其实相当于一种倍增。
比如说有一件物品价值为3,数量为10,可以把10进行二进制拆分1,2,4,3。这4个数能够组成【1,10】内任意一个数,并且组合成的所有数恰好填满此区间,也就说不可能组合成除此区间外的任何一个数,这就保证了问题的性质不变。
推广到一般化,拆分方法为 把 n[i] 拆分成 20 21 22 23 ......2k , t初始值为 n[i] 每拆一个就更新t = t - 2k 最后不能再拆时满足 t < 2k+1
【AC代码】

//二进制优化 #include<iostream> #include<cstring> using namespace std; const int maxn = 1e3+10; int w[maxn]; int c[maxn]; int s[maxn]; int n,v; int cnt;//二进制转化 后的物品数量 int dp[6*maxn];//dp[i]表示背包体积为i时获得的最大价值 int main(){ int t; int price, value, quantity; while(cin>>n>>v){ cnt = 0; memset(dp, 0 ,sizeof dp); //读入价值 for(int i=1; i<=n; i++){ cin>>price>>value>>quantity; //进行二进制优化 转化成0-1背包 int t = 1; while(quantity >= t){ c[++cnt] = price * t; w[cnt] = value * t; quantity -= t; t*=2; } //别忘了最后可能有剩余 if(quantity > 0) { c[++cnt] = price * quantity; w[cnt] = value * quantity; } } //注意i的上限是cnt不是n了 for(int i=1; i<=cnt; i++){ for(int j=v; j>=c[i]; j--){ dp[j] = max(dp[j-c[i]] + w[i], dp[j]); } } cout<<dp[v]<<endl; } }
