1、蒙特卡罗算法
基本概述
蒙特卡罗(Monte Carlo)方法,又称随机抽样或统计试验方法。传统的经验方法由于不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡罗方法由于能够真实地模拟实际物理过程,故解决问题与实际非常符合,可以得到很圆满的结果。
在实际应用中常会遇到一些问题,不论采用确定性算法或概率算法都无法保证每次都能得到正确的解答。蒙特卡罗算法则在一般情况下可以保证对问题的所有实例都以高概率给出正确解,但是通常无法判定一个具体解是否正确。
设p是一个实数,且1/2<p<1。如果一个蒙特卡罗算法对于问题的任一实例得到正确解的概率不小于p,则称该蒙特卡罗算法是p正确的,且称p-1/2是该算法的优势。
如果对于同一实例,蒙特卡罗算法不会给出2个不同的正确解答,则称该蒙特卡罗算法是一致的。
有些蒙特卡罗算法除了具有描述问题实例的输入参数外,还具有描述错误解可接受概率的参数。这类算法的计算时间复杂性通常由问题的实例规模以及错误解可接受概率的函数来描述。
对于一个一致的P正确蒙特卡罗算法,要提高获得正确率的概率,只要执行该算法若干次,并选择出现频次最高的解即可。
原理思想
当所要求解的问题是某种事件出现的概率,或者是某个随机变量的期望值时,它们可以通过某种“试验”的方法,得到这种事件出现的频率,或者这个随机变数的平均值,并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征,利用数学方法来加以模拟,即进行一种数字模拟实验。它是以一个概率模型为基础,按照这个模型所描绘的过程,通过模拟实验的结果,作为问题的近似解。
主要步骤
蒙特卡罗解题归结为三个主要步骤:构造或描述概率过程;实现从已知概率分布抽样;建立各种估计量。
1)构造或描述概率过程: 对于本身就具有随机性质的问题,如粒子输运问题,主要是正确描述和模拟这个概率过程,对于本来不是随机性质的确定性问题,比如计算定积分,就必须事先构造一个人为的概率过程,它的某些参量正好是所要求问题的解。即要将不具有随机性质的问题转化为随机性质的问题。
2)实现从已知概率分布抽样: 构造了概率模型以后,由于各种概率模型都可以看作是由各种各样的概率分布构成的,因此产生已知概率分布的随机变量(或随机向量),就成为实现蒙特卡罗方法模拟实验的基本手段,这也是蒙特卡罗方法被称为随机抽样的原因。最简单、最基本、最重要的一个概率分布是(0,1)上的均匀分布(或称矩形分布)。随机数就是具有这种均匀分布的随机变量。随机数序列就是具有这种分布的总体的一个简单子样,也就是一个具有这种分布的相互独立的随机变数序列。产生随机数的问题,就是从这个分布的抽样问题。在计算机上,可以用物理方法产生随机数,但价格昂贵,不能重复,使用不便。另一种方法是用数学递推公式产生。这样产生的序列,与真正的随机数序列不同,所以称为伪随机数,或伪随机数序列。不过,经过多种统计检验表明,它与真正的随机数,或随机数序列具有相近的性质,因此可把它作为真正的随机数来使用。由已知分布随机抽样有各种方法,与从(0,1)上均匀分布抽样不同,这些方法都是借助于随机序列来实现的,也就是说,都是以产生随机数为前提的。由此可见,随机数是我们实现蒙特卡罗模拟的基本工具。 建立各种估计量: 一般说来,构造了概率模型并能从中抽样后,即实现模拟实验后,我们就要确定一个随机变量,作为所要求的问题的解,我们称它为无偏估计。
3)建立各种估计量:相当于对模拟实验的结果进行考察和登记,从中得到问题的解。
2、主元素问题
问题描述
设T[1:n]是一个含有n个元素的数组。当|{i|T[i]=x}|>n/2时,称元素x是数组T的主元素。 例如:数组T[]={5,5,5,5,5,5,1,3,4,6}中,元素T[0:5]为数组T[]的主元素。
问题求解
算法随机选择数组元素x,由于数组T的非主元素个数小于n/2,所以,x不为主元素的概率小于1/2。因此判定数组T的主元素存在性的算法是一个偏真1/2正确的算法。50%的错误概率是不可容忍的,利用重复调用技术将错误概率降低到任何可接受的范围内。对于任何给定的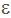
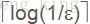
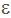
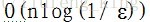
代码实现:

//随机化算法 蒙特卡罗算法 主元素问题 //#include "stdafx.h" #include "RandomNumber.h" #include <cmath> #include <iostream> using namespace std; //判定主元素的蒙特卡罗算法 template<class Type> bool Majority(Type *T,int n) { RandomNumber rnd; int i = rnd.Random(n); Type x = T[i]; //随机选择数组元素 int k = 0; for(int j=0; j<n; j++) { if(T[j] == x) { k++; } } return (k>n/2); //k>n/2时,T含有主元素 } //重复k次调用算法Majority template<class Type> bool MajorityMC(Type *T,int n,double e) { int k = ceil(log(1/e)/log((float)2)); for(int i=1; i<=k; i++) { if(Majority(T,n)) { return true; } } return false; } int main() { int n = 10; float e = 0.001; int a[] = {5,5,5,5,5,5,1,3,4,6}; cout<<"数组a的元素如下:"<<endl; for(int i=0; i<10; i++) { cout<<a[i]<<" "; } cout<<endl; cout<<"调用MajorityMC判断数组是否含有主元素结果是:"<<MajorityMC(a,n,e)<<endl; }

#include"time.h" //随机数类 const unsigned long maxshort = 65536L; const unsigned long multiplier = 1194211693L; const unsigned long adder = 12345L; class RandomNumber { private: //当前种子 unsigned long randSeed; public: RandomNumber(unsigned long s = 0);//构造函数,默认值0表示由系统自动产生种子 unsigned short Random(unsigned long n);//产生0:n-1之间的随机整数 double fRandom(void);//产生[0,1)之间的随机实数 }; RandomNumber::RandomNumber(unsigned long s)//产生种子 { if(s == 0) { randSeed = time(0);//用系统时间产生种子 } else { randSeed = s;//由用户提供种子 } } unsigned short RandomNumber::Random(unsigned long n)//产生0:n-1之间的随机整数 { randSeed = multiplier * randSeed + adder;//线性同余式 return (unsigned short)((randSeed>>16)%n); } double RandomNumber::fRandom(void)//产生[0,1)之间的随机实数 { return Random(maxshort)/double(maxshort); }
实现结果:
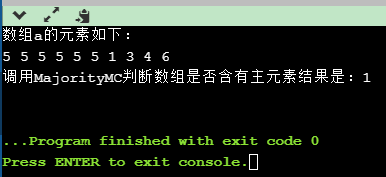
参考文献:王晓东《算法设计与分析》
https://blog.csdn.net/liufeng_king/article/details/9251589
