《统计学习方法》第六章，逻辑斯蒂回归

▶ 使用逻辑地模型来进行分类，可以算出每个测试样本分属于每个类别的概率

● 二分类代码

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from matplotlib.patches import Rectangle

dataSize = 10000
trainRatio = 0.3
ita = 0.03                                                  # 学习效率
epsilon = 0.01
defaultTurn = 200                                           # 默认最大学习轮数
colors = [[0.5,0.25,0],[1,0,0],[0,0.5,0],[0,0,1],[1,0.5,0]] # 棕红绿蓝橙
trans = 0.5

def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

def function(x, para):                                      # 回归函数
    return sigmoid(np.sum(x * para[0]) + para[1])

def judge(x, para):                                         # 分类函数，用 0.5 做分界
    return int(function(x, para) > 0.5)

def dataSplit(x, y, part):    
    return x[:part], y[:part],x[part:],y[part:]

def createData(dim, count = dataSize):                                      # 创建数据集
    np.random.seed(103)       
    X = np.random.rand(count, dim)
    Y = ((3 - 2 * dim)*X[:,0] + 2 * np.sum(X[:,1:], 1) > 0.5).astype(int)   # 只考虑 {0，1} 的二分类         
    class1Count = 0
    for i in range(count):
        class1Count += (Y[i] + 1)>>1   
    print("dim = %d, dataSize = %d, class 1 ratio -> %4f"%(dim, count, class1Count / count))
    return X, Y

def gradientDescent(dataX, dataY, turn = defaultTurn):                      # 梯度下降法
    count, dim = np.shape(dataX)
    xE = np.concatenate((dataX, np.ones(count)[:,np.newaxis]), axis = 1)    # 补充最后一列的 1 作为零次项
    w = np.ones(dim + 1)    
    
    for t in range(turn):        
        y = sigmoid(np.dot(xE, w).T)                                        # 尺寸：xE:count*(dim+1)，w:(dim+1)*1，y:1*count
        error = dataY - y                                                   # 尺寸：error:1*count
        w += ita * np.dot(error, xE)                                        # 尺寸：w:1*(dim+1)
        if np.sum(error * error) < count * epsilon:                         #if np.sum(error * error) / count < epsilon:
            break   
    return (w[:-1], w[-1])

def test(dim):                                                
    allX, allY = createData(dim)
    trainX, trainY, testX, testY = dataSplit(allX, allY, int(dataSize * trainRatio))
    
    para = gradientDescent(testX, testY)                                    # 训练   
    
    myResult = [ judge(x, para) for x in testX]                              
    errorRatio = np.sum((np.array(myResult) - testY)**2) / (dataSize * (1 - trainRatio))
    print("dim = %d, errorRatio = %4f
"%(dim, errorRatio))
    
    if dim >= 4:                                                            # 4维以上不画图，只输出测试错误率
        return
    errorPX = []                                                            # 测试数据集分为错误类，1 类和 0 类
    errorPY = []
    class1 = []
    class0 = []
    for i in range(len(testX)):
        if myResult[i] != testY[i]:
            errorPX.append(testX[i])
            errorPY.append(testY[i])
        elif myResult[i] == 1:
            class1.append(testX[i])
        else:
            class0.append(testX[i])
    errorPX = np.array(errorPX)
    errorPY = np.array(errorPY)
    class1 = np.array(class1)
    class0 = np.array(class0)

    fig = plt.figure(figsize=(10, 8))                  
    
    if dim == 1:
        plt.xlim(0.0,1.0)
        plt.ylim(-0.25,1.25)
        plt.plot([0.5, 0.5], [-0.5, 1.25], color = colors[0],label = "realBoundary")               
        plt.plot([0, 1], [ function(i, para) for i in [0,1] ],color = colors[4], label = "myF")
        plt.scatter(class1, np.ones(len(class1)), color = colors[1], s = 2,label = "class1Data")               
        plt.scatter(class0, np.zeros(len(class0)), color = colors[2], s = 2,label = "class0Data")               
        if len(errorPX) != 0:
            plt.scatter(errorPX, errorPY,color = colors[3], s = 16,label = "errorData")       
        plt.text(0.21, 1.12, "realBoundary: 2x = 1
myF(x) = " + str(round(para[0][0],2)) + " x + " + str(round(para[1],2)) + "
 errorRatio = " + str(round(errorRatio,4)),
            size=15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.)))
        R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(5)]
        plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData", "myF"], loc=[0.81, 0.2], ncol=1, numpoints=1, framealpha = 1)       
   
    if dim == 2:       
        plt.xlim(0.0,1.0)
        plt.ylim(0.0,1.0)
        plt.plot([0,1], [0.25,0.75], color = colors[0],label = "realBoundary")       
        xx = np.arange(0, 1 + 0.1, 0.1)               
        X,Y = np.meshgrid(xx, xx)
        contour = plt.contour(X, Y, [ [ function((X[i,j],Y[i,j]), para) for j in range(11)] for i in range(11) ])
        plt.clabel(contour, fontsize = 10,colors='k')
        plt.scatter(class1[:,0], class1[:,1], color = colors[1], s = 2,label = "class1Data")       
        plt.scatter(class0[:,0], class0[:,1], color = colors[2], s = 2,label = "class0Data")       
        if len(errorPX) != 0:
            plt.scatter(errorPX[:,0], errorPX[:,1], color = colors[3], s = 8,label = "errorData")       
        plt.text(0.71, 0.92, "realBoundary: -x + 2y = 1/2
myF(x,y) = " + str(round(para[0][0],2)) + " x + " + str(round(para[0][1],2)) + " y + " + str(round(para[1],2)) + "
 errorRatio = " + str(round(errorRatio,4)), 
            size = 15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.)))
        R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(4)]
        plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData"], loc=[0.81, 0.2], ncol=1, numpoints=1, framealpha = 1)    

    if dim == 3:       
        ax = Axes3D(fig)
        ax.set_xlim3d(0.0, 1.0)
        ax.set_ylim3d(0.0, 1.0)
        ax.set_zlim3d(0.0, 1.0)
        ax.set_xlabel('X', fontdict={'size': 15, 'color': 'k'})
        ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'k'})
        ax.set_zlabel('W', fontdict={'size': 15, 'color': 'k'})
        v = [(0, 0, 0.25), (0, 0.25, 0), (0.5, 1, 0), (1, 1, 0.75), (1, 0.75, 1), (0.5, 0, 1)]
        f = [[0,1,2,3,4,5]]
        poly3d = [[v[i] for i in j] for j in f]
        ax.add_collection3d(Poly3DCollection(poly3d, edgecolor = 'k', facecolors = colors[0]+[trans], linewidths=1))       
        ax.scatter(class1[:,0], class1[:,1],class1[:,2], color = colors[1], s = 2, label = "class1")                      
        ax.scatter(class0[:,0], class0[:,1],class0[:,2], color = colors[2], s = 2, label = "class0")                      
        if len(errorPX) != 0:
            ax.scatter(errorPX[:,0], errorPX[:,1],errorPX[:,2], color = colors[3], s = 8, label = "errorData")               
        ax.text3D(0.74, 0.95, 1.15, "realBoundary: -3x + 2y +2z = 1/2
myF(x,y,z) = " + str(round(para[0][0],2)) + " x + " + 
            str(round(para[0][1],2)) + " y + " + str(round(para[0][2],2)) + " z + " + str(round(para[1],2)) + "
 errorRatio = " + str(round(errorRatio,4)), 
            size = 12, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1, 0.5, 0.5), fc=(1, 1, 1)))
        R = [Rectangle((0,0),0,0, color = colors[k]) for k in range(4)]
        plt.legend(R, ["realBoundary", "class1Data", "class0Data", "errorData"], loc=[0.83, 0.1], ncol=1, numpoints=1, framealpha = 1)
       
    fig.savefig("R:\dim" + str(dim) + ".png")
    plt.close() 

if __name__=='__main__':
    test(1)        
    test(2)        
    test(3)           
    test(4)
    test(5)

● 输出结果

dim = 1, dataSize = 10000, class 1 ratio -> 0.509000
dim = 1, errorRatio = 0.015000

dim = 2, dataSize = 10000, class 1 ratio -> 0.496000
dim = 2, errorRatio = 0.008429

dim = 3, dataSize = 10000, class 1 ratio -> 0.498200
dim = 3, errorRatio = 0.012429

dim = 4, dataSize = 10000, class 1 ratio -> 0.496900
dim = 4, errorRatio = 0.012857

dim = 5, dataSize = 10000, class 1 ratio -> 0.500000
dim = 5, errorRatio = 0.012143

● 画图

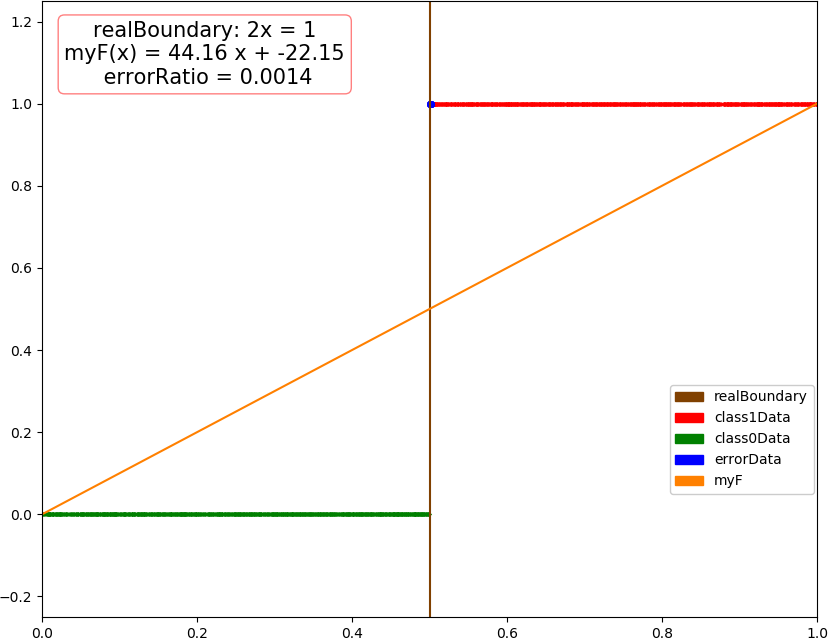
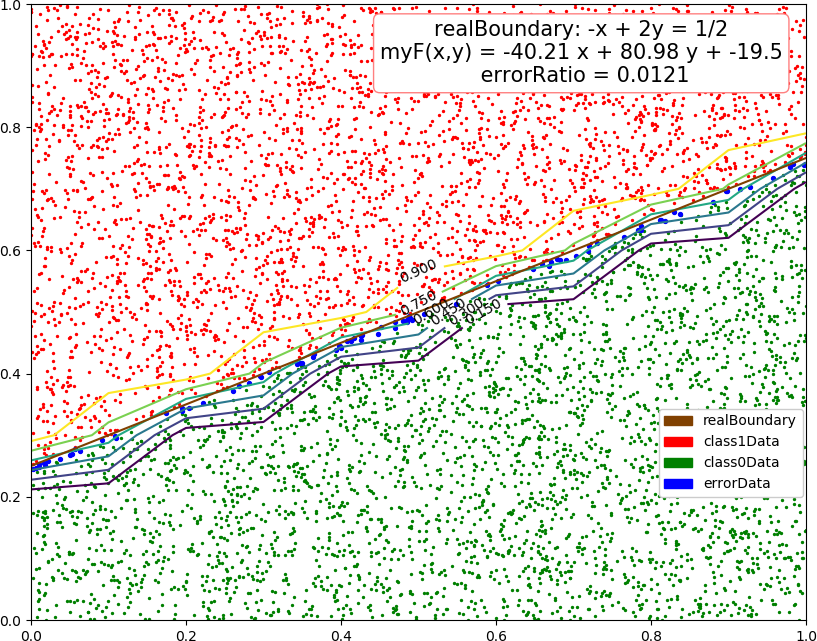
● 补充，从【https://www.cnblogs.com/zhizhan/p/4868555.html】了解到，低度下降方法的变种

# 梯度下降法
weight += alpha * dataX.T * ( dataY - sigmoid(dataXx * weight) )

# Stochastic 梯度下降法，每次取一个样本
for i in range(numSamples):  
    weight += ita * dataX[i].T * ( dataY[i] - sigmoid(dataXx[i] * weight) )

# 平滑 Stochastic 低度下降法，学习效率逐渐递减，并保证有下限 0.01         
indexList = range(count)                                # count 为样本数
for i in range(count):                                  
    ita = 0.01 + 4.0 / (1.0 + t + i)                    # t 为 轮数
    index = np.random.choice(indexList)
    weight += ita * dataX[index].T * ( dataY[index] - sigmoid(train_x[index] * weight) )
    del(indexList[index])                               # 单轮学习中样本只用一次