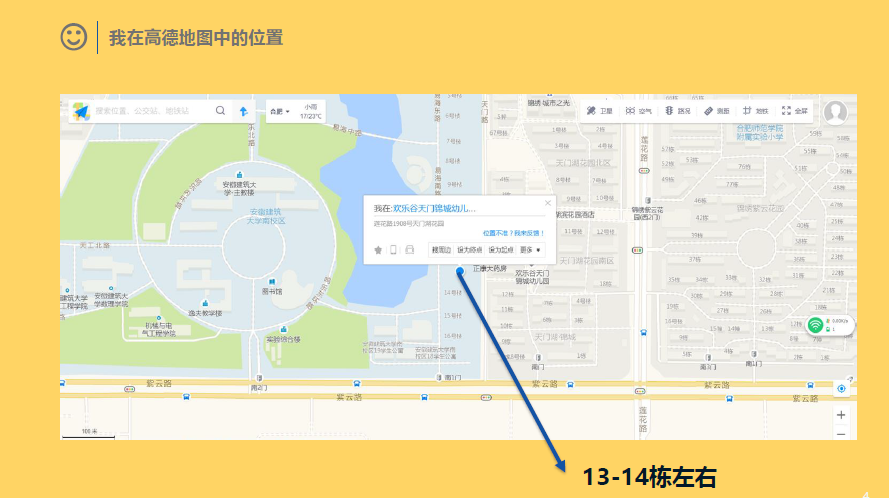
说明:物联网定位技术课程,PPT汇报,结合各类定位技术,这里我主要对KNN和三边定位进行说明,其中三边(三角)定位在最近的网剧《白夜追凶》中频繁出现,遂结合IP,进行研究讨论。
标题《我眼中的定位算法》





















☆ KNN算法介绍
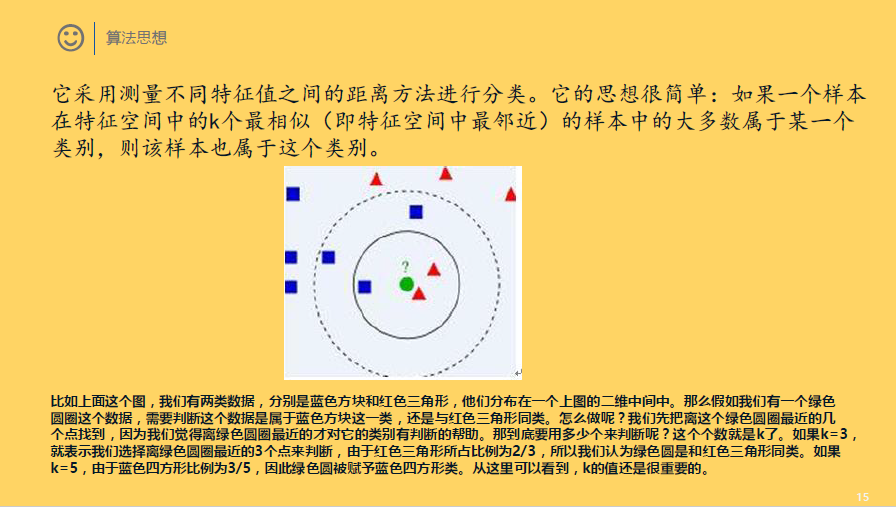
它采用测量不同特征值之间的距离方法进行分类。它的思想很简单:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
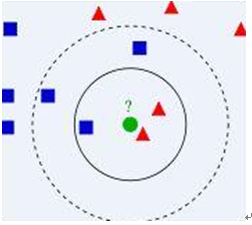
比如上面这个图,我们有两类数据,分别是蓝色方块和红色三角形,他们分布在一个上图的二维中间中。那么假如我们有一个绿色圆圈这个数据,需要判断这个数据是属于蓝色方块这一类,还是与红色三角形同类。怎么做呢?我们先把离这个绿色圆圈最近的几个点找到,因为我们觉得离绿色圆圈最近的才对它的类别有判断的帮助。那到底要用多少个来判断呢?这个个数就是k了。如果k=3,就表示我们选择离绿色圆圈最近的3个点来判断,由于红色三角形所占比例为2/3,所以我们认为绿色圆是和红色三角形同类。如果k=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。从这里可以看到,k的值还是很重要的。
KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。由于KNN方法主要靠周围有限的邻近的样本,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
当我们已经存在了一个带标签的数据库,然后输入没有标签的新数据后,将新数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似(最近邻)的分类标签。一般来说,只选择样本数据库中前k个最相似的数据。最后,选择k个最相似数据中出现次数最多的分类。其算法描述如下:
1)计算已知类别数据集中的点与当前点之间的距离;
2)按照距离递增次序排序;
3)选取与当前点距离最小的k个点;
4)确定前k个点所在类别的出现频率;
5)返回前k个点出现频率最高的类别作为当前点的预测分类。
△ 基于RSS指纹的室内定位的KNN算法实现:
%% KNN算法
n = 6;%使用AP的数目,这里使用全部6个(<=n_AP)
k = 4;%KNN算法中的K,
p_KNN = 0;%存定位结果
for i=1:size(p_true); %按顺序分别给每一个数据定位
[size_x, size_y, n_AP] = size(fingerprint_sim); %计算欧氏距离
distance = 0;
for j=1:n
distance = distance + (fingerprint_sim(:,:,j)-RSS_fp(i,j)).^2;%这里同时计算所有参考点,结果是一个二维矩阵
end
distance = sqrt(distance);
%将欧氏距离排序,选择k个最小的,得到位置
d = reshape(distance,1,size_x*size_y);
[whatever, index_d]=sort(d);
knn_x = (mod(index_d(1:k),size_x));
knn_y = (floor(index_d(1:k)./size_x)+1);
p_KNN(i,1:2) = [mean(knn_x), mean(knn_y)];%k个位置求平均
end
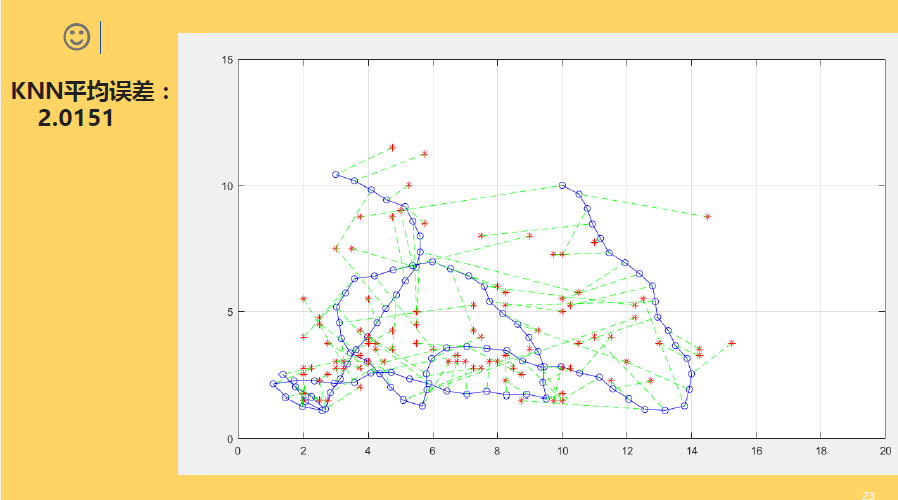
%画一下图:蓝色的线b-o是真实路径,红星是定位算出的位置
plot(p_true(:,1),p_true(:,2),'b-o');
axis([0 20 0 15])
grid on;hold on;
plot(p_KNN(:,1),p_KNN(:,2),'r*');
for i=1:size(p_KNN)
hold on;plot([p_KNN(i,1),p_true(i,1)],[p_KNN(i,2),p_true(i,2)],'g--');
end
error_KNN=sqrt((p_true(:,1)-p_KNN(:,1)).^2+(p_true(:,2)-p_KNN(:,2)).^2);
disp('KNN平均误差:')
disp(mean(error_KNN));
△ KNN的实现
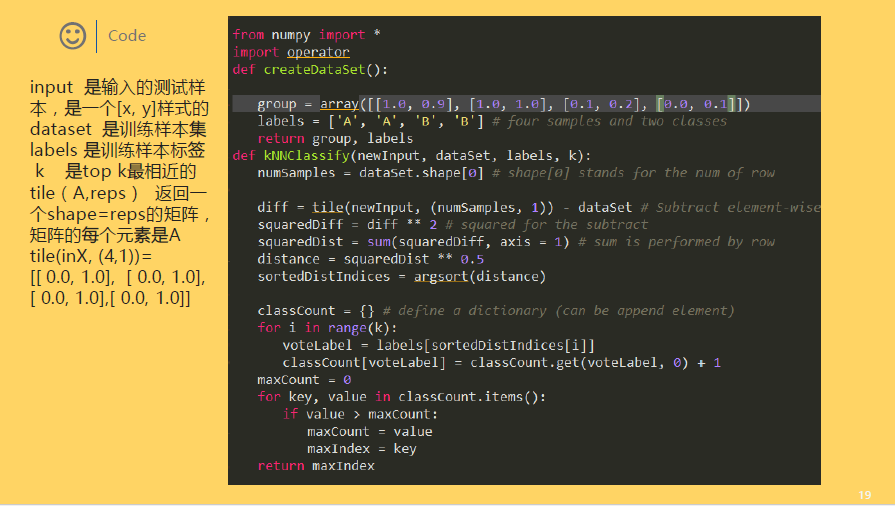
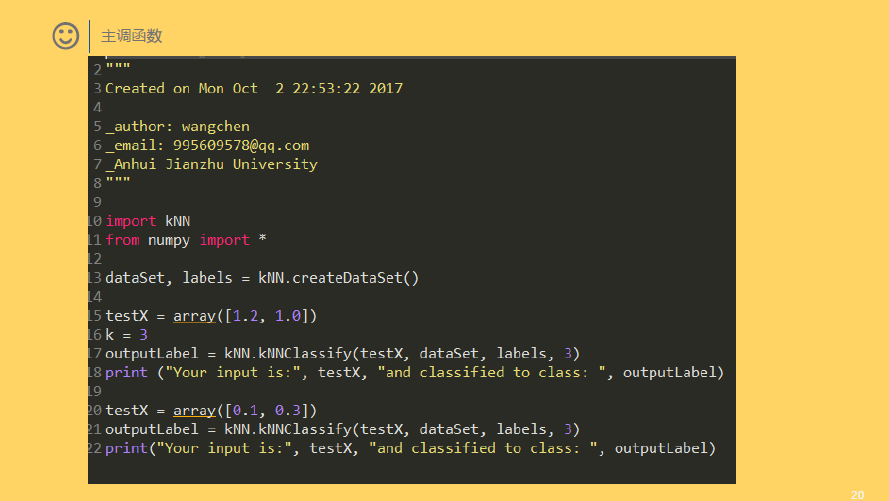
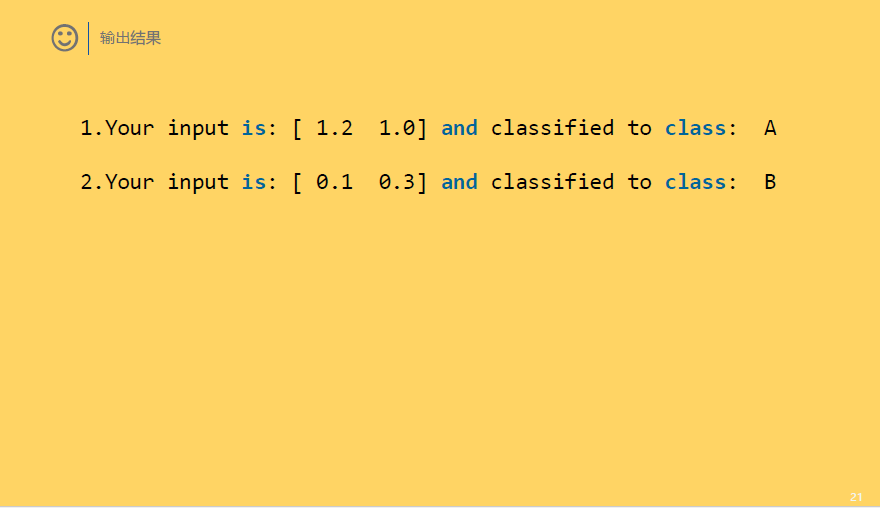
1 # -*- coding: utf-8 -*- 2 """python实现KNN 3 Created on Tue Oct 3 09:13:54 2017 4 5 _author: wangchen 6 _email: 995609578@qq.com 7 _Anhui Jianzhu University 8 """ 9 10 11 #coding=UTF8 12 from numpy import * 13 import operator 14 15 def createDataSet(): 16 """ 17 函数作用:构建一组训练数据(训练样本),共4个样本 18 同时给出了这4个样本的标签,及labels 19 """ 20 group = array([ 21 [1.0, 1.1], 22 [1.0, 1.0], 23 [0. , 0. ], 24 [0. , 0.1] 25 ]) 26 labels = ['A', 'A', 'B', 'B'] 27 return group, labels 28 29 def classify0(inX, dataset, labels, k): 30 """ 31 inX 是输入的测试样本,是一个[x, y]样式的 32 dataset 是训练样本集 33 labels 是训练样本标签 34 k 是top k最相近的 35 """ 36 # shape返回矩阵的[行数,列数], 37 # 那么shape[0]获取数据集的行数, 38 # 行数就是样本的数量 39 dataSetSize = dataset.shape[0] 40 41 """ 42 下面的求距离过程就是按照欧氏距离的公式计算的。 43 即 根号(x^2+y^2) 44 """ 45 # tile属于numpy模块下边的函数 46 # tile(A, reps)返回一个shape=reps的矩阵,矩阵的每个元素是A 47 # 比如 A=[0,1,2] 那么,tile(A, 2)= [0, 1, 2, 0, 1, 2] 48 # tile(A,(2,2)) = [[0, 1, 2, 0, 1, 2], 49 # [0, 1, 2, 0, 1, 2]] 50 # tile(A,(2,1,2)) = [[[0, 1, 2, 0, 1, 2]], 51 # [[0, 1, 2, 0, 1, 2]]] 52 # 上边那个结果的分开理解就是: 53 # 最外层是2个元素,即最外边的[]中包含2个元素,类似于[C,D],而此处的C=D,因为是复制出来的 54 # 然后C包含1个元素,即C=[E],同理D=[E] 55 # 最后E包含2个元素,即E=[F,G],此处F=G,因为是复制出来的 56 # F就是A了,基础元素 57 # 综合起来就是(2,1,2)= [C, C] = [[E], [E]] = [[[F, F]], [[F, F]]] = [[[A, A]], [[A, A]]] 58 # 这个地方就是为了把输入的测试样本扩展为和dataset的shape一样,然后就可以直接做矩阵减法了。 59 # 比如,dataset有4个样本,就是4*2的矩阵,输入测试样本肯定是一个了,就是1*2,为了计算输入样本与训练样本的距离 60 # 那么,需要对这个数据进行作差。这是一次比较,因为训练样本有n个,那么就要进行n次比较; 61 # 为了方便计算,把输入样本复制n次,然后直接与训练样本作矩阵差运算,就可以一次性比较了n个样本。 62 # 比如inX = [0,1],dataset就用函数返回的结果,那么 63 # tile(inX, (4,1))= [[ 0.0, 1.0], 64 # [ 0.0, 1.0], 65 # [ 0.0, 1.0], 66 # [ 0.0, 1.0]] 67 # 作差之后 68 # diffMat = [[-1.0,-0.1], 69 # [-1.0, 0.0], 70 # [ 0.0, 1.0], 71 # [ 0.0, 0.9]] 72 diffMat = tile(inX, (dataSetSize, 1)) - dataset 73 74 # diffMat就是输入样本与每个训练样本的差值,然后对其每个x和y的差值进行平方运算。 75 # diffMat是一个矩阵,矩阵**2表示对矩阵中的每个元素进行**2操作,即平方。 76 # sqDiffMat = [[1.0, 0.01], 77 # [1.0, 0.0 ], 78 # [0.0, 1.0 ], 79 # [0.0, 0.81]] 80 sqDiffMat = diffMat ** 2 81 82 # axis=1表示按照横轴,sum表示累加,即按照行进行累加。 83 # sqDistance = [[1.01], 84 # [1.0 ], 85 # [1.0 ], 86 # [0.81]] 87 sqDistance = sqDiffMat.sum(axis=1) 88 89 # 对平方和进行开根号 90 distance = sqDistance ** 0.5 91 92 # 按照升序进行快速排序,返回的是原数组的下标。 93 # 比如,x = [30, 10, 20, 40] 94 # 升序排序后应该是[10,20,30,40],他们的原下标是[1,2,0,3] 95 # 那么,numpy.argsort(x) = [1, 2, 0, 3] 96 sortedDistIndicies = distance.argsort() 97 98 # 存放最终的分类结果及相应的结果投票数 99 classCount = {} 100 101 # 投票过程,就是统计前k个最近的样本所属类别包含的样本个数 102 for i in range(k): 103 # index = sortedDistIndicies[i]是第i个最相近的样本下标 104 # voteIlabel = labels[index]是样本index对应的分类结果('A' or 'B') 105 voteIlabel = labels[sortedDistIndicies[i]] 106 # classCount.get(voteIlabel, 0)返回voteIlabel的值,如果不存在,则返回0 107 # 然后将票数增1 108 classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 109 110 # 把分类结果进行排序,然后返回得票数最多的分类结果,python3.5,没有iteritems,改为items 111 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) 112 return sortedClassCount[0][0] 113 114 if __name__== "__main__": 115 # 导入数据 116 dataset, labels = createDataSet() 117 inX = [0.1, 0.1] 118 # 简单分类 119 className = classify0(inX, dataset, labels, 3) 120 print ('the class of ', inX,'test sample is %s' %className)