[LOJ 6058]百步穿杨

题目

点这里看题目。

分析

建图有两个重要的条件需要注意：

1. 弹道可能变成了折线；
2. 控制每个格子最多被穿过一次；

常规的最大流/费用流做法不方便处理第一个点，我们不妨尝试最小割。

第二个点就意味着，每个格子要么被纵向穿过，要么被横向穿过。此时每个格子就存在两种选择，恰好对应 " 属于 (S) " 和 " 属于 (T) " 两种情况。

那么进一步思考，最小割的初始值是多少？当然是每个箭塔的攻击方向上的最大分值。

取到最大分值的要求是，路径上的格子都要被箭矢的方向穿过，中途有一格断了都不行。于是可以考虑对攻击路线上的所有格子设置边的代价。

考虑攻击方向上的格子 (u) 和下一个格子 (v) ，应该如何限制。首先我们已经有了基本图：

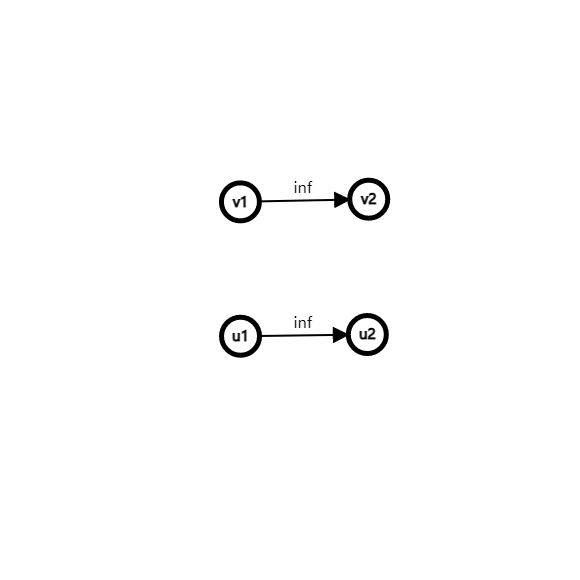
考虑，如果 (u_1) 选择在 (S) 集合，我们就认为它是纵向穿过，否则是横向穿过。现在有一支箭矢纵向穿过，那么 (u_1) 属于 (S) 集合，而 (v_1) 属于 (T) 集合时，这只箭就无法射出，我们需要计算代价 (w) ，接着连接 (u_1 ightarrow v_1) ，容量为 (w) ，表示必须要花费这样的代价。注意，如果 (u) 上面本身就有一个箭靶，我们应该计算它带来的贡献。

对于一个纵向的箭塔 (u) ，它必须属于 (S) 集合，因此连接 (S ightarrow u) ，容量为 (infty) 。同理，对于横向应连出 (v ightarrow T) ，容量为 (infty) 。

建完就可以开始跑最大流啦。

小结：

利用每个格子只能横向或纵向这样的选择，从而联系到了 " 属于 (S) " 和 " 属于 (T) " 两种情况；接着便可以利用二元关系建图。

代码

#include <cstdio>
#include <cstring>

const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 5, MAXM = 1e6 + 5;
const int MAXS = 105;

template<typename _T>
void read( _T &x )
{
	x = 0; char s = getchar(); int f = 1;
	while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
	while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ) putchar( '-' ), x = -x;
	if( 9 < x ) write( x / 10 );
	putchar( x % 10 + '0' );
}

template<typename _T>
_T MIN( const _T a, const _T b )
{
	return a < b ? a : b;
}

template<typename _T>
_T MAX( const _T a, const _T b )
{
	return a > b ? a : b;
}

struct Edge
{
	int to, nxt, c;
}Graph[MAXM << 1];

int dir[4][2] = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };

char tower[256];

int q[MAXN];

char S[MAXS][MAXS];

int head[MAXN], dep[MAXN], cur[MAXN];
int N, M, cnt = 1, tot;

void AddEdge( const int from, const int to, const int C )
{
	Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
	Graph[cnt].c = C, head[from] = cnt;
}

#define In( x, y ) ( ( x - 1 ) * M + y )
#define Out( x, y ) ( ( x - 1 ) * M + y + N * M )

bool Inside( const int x, const int y ) { return 1 <= x && x <= N && 1 <= y && y <= M; }
void AddE( const int from, const int to, const int C ) { AddEdge( from, to, C ), AddEdge( to, from, 0 ); }

bool BFS( const int S, const int T )
{
	int h = 1, t = 0, u, v;
	for( int i = 1 ; i <= tot ; i ++ ) dep[i] = INF;
	dep[q[++ t] = S] = 0;
	while( h <= t )
	{
		u = q[h ++];
		for( int i = head[u] ; i ; i = Graph[i].nxt )
			if( Graph[i].c && dep[v = Graph[i].to] > dep[u] + 1 )
				dep[q[++ t] = v] = dep[u] + 1;
	}
	return dep[T] < INF;
}

int DFS( const int u, const int lin, const int T )
{
	if( u == T ) return lin;
	int used = 0, ret, v, c;
	for( int &i = cur[u] ; i ; i = Graph[i].nxt )
	{
		v = Graph[i].to, c = Graph[i].c;
		if( dep[v] == dep[u] + 1 && c && ( ret = DFS( v, MIN( lin - used, c ), T ) ) )
		{
			used += ret, Graph[i].c -= ret, Graph[i ^ 1].c += ret;
			if( used == lin ) break;
		}
	}
	if( used < lin ) dep[u] = INF;
	return used;
}

int Dinic( const int S, const int T )
{
	int f = 0;
	while( BFS( S, T ) )
	{
		for( int i = 1 ; i <= tot ; i ++ ) cur[i] = head[i];
		f += DFS( S, INF, T );
	}
	return f;
}

int main()
{
	memset( tower, -1, sizeof tower );
	tower['A'] = 0, tower['V'] = 1, tower['<'] = 2, tower['>'] = 3;
	read( N ), read( M ), tot = ( N * M ) << 1;
	const int s = ++ tot, t = ++ tot; int ans = 0;
	for( int i = 1 ; i <= N ; i ++ ) scanf( "%s", S[i] + 1 );
	for( int i = 1 ; i <= N ; i ++ )
		for( int j = 1 ; j <= M ; j ++ )
		{
			int d;
			AddE( In( i, j ), Out( i, j ), INF );
			if( ~ ( d = tower[S[i][j]] ) )
			{
				int x, y, val = 0;
				if( d < 2 ) AddE( s, In( i, j ), INF );
				else AddE( Out( i, j ), t, INF );
				for( x = i, y = j ; Inside( x, y ) ; x += dir[d][0], y += dir[d][1] )
					if( '0' <= S[x][y] && S[x][y] <= '9' ) val = MAX( val, S[x][y] - '0' );
				ans += val, x = i + dir[d][0], y = j + dir[d][1];
				if( Inside( x, y ) )
				{
					if( d < 2 ) AddE( In( i, j ), In( x, y ), val );
					else AddE( Out( x, y ), Out( i, j ), val );
					for( ; Inside( x + dir[d][0], y + dir[d][1] ) ; x += dir[d][0], y += dir[d][1] )
					{
						int coe;
						if( '0' <= S[x][y] && S[x][y] <= '9' ) coe = val - S[x][y] + '0';
						else coe = val;
						if( d < 2 ) AddE( In( x, y ), In( x + dir[d][0], y + dir[d][1] ), coe );
						else AddE( Out( x + dir[d][0], y + dir[d][1] ), Out( x, y ), coe );
					}
				}
			}
		}
	write( ans - Dinic( s, t ) ), putchar( '
' );
	return 0;
}