对称二叉树
题目描述
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
- 二叉树;
- 将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值,节点外的 (id) 表示节点编号。
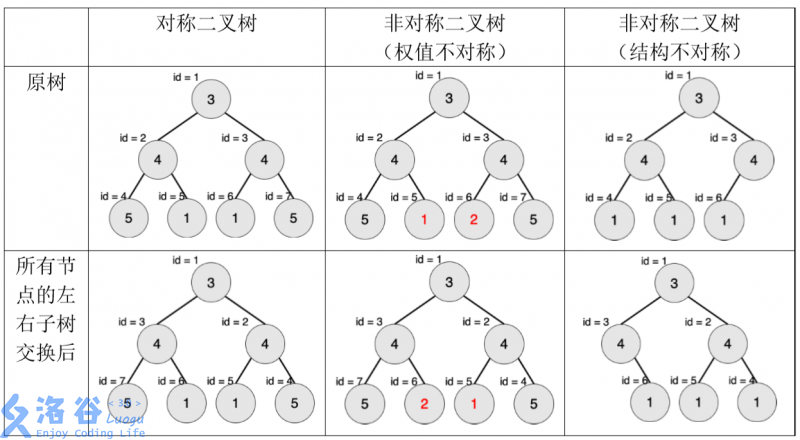
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 (T) 为子树根的一棵"子 树"指的是:节点(T) 和它的全部后代节点构成的二叉树。
输入输出格式
输入格式
第一行一个正整数 (n),表示给定的树的节点的数目,规定节点编号 (1 sim n),其中节点 (1) 是树根。
第二行 (n) 个正整数,用一个空格分隔,第 (i) 个正整数 (v_i) 代表节点 (i) 的权值。
接下来 (n) 行,每行两个正整数 (l_i, r_i),分别表示节点 (i) 的左右孩子的编号。如果不存在左 / 右孩子,则以 (-1) 表示。两个数之间用一个空格隔开。
输出格式
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
输入输出样例
输入样例 #1
2
1 3
2 -1
-1 -1
输出样例 #1
1
输入样例 #2
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8
输出样例 #2
3
说明
【输入输出样例 1 说明】
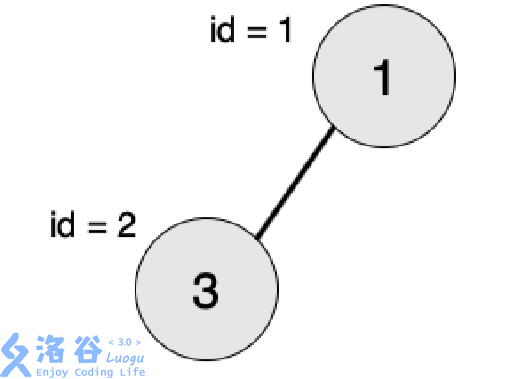
最大的对称二叉子树为以节点 (2) 为树根的子树,节点数为 (1)。
【输入输出样例 2 说明】
 最大的对称二叉子树为以节点 (7) 为树根的子树,节点数为 (3)。
最大的对称二叉子树为以节点 (7) 为树根的子树,节点数为 (3)。
【数据规模与约定】 共 (25) 个测试点。 (v_i ≤ 1000)。
测试点 (1 sim 3, n ≤ 10),保证根结点的左子树的所有节点都没有右孩子,根结点的右 子树的所有节点都没有左孩子。
测试点 (4 sim 8, n ≤ 10)。 测试点 (9 sim 12, n ≤ 10^5),保证输入是一棵"满二叉树" 。
测试点 (13 sim 16, n ≤ 10^5),保证输入是一棵"完全二叉树"。
测试点 (17 sim 20, n ≤ 10^5),保证输入的树的点权均为 (1)。
测试点 (21 sim 25, n ≤ 10^6)。
本题约定:
层次:节点的层次从根开始定义起,根为第一层,根的孩子为第二层。树中任一节 点的层次等于其父亲节点的层次加 (1)。
树的深度:树中节点的最大层次称为树的深度。
满二叉树:设二叉树的深度为 (h),且二叉树有 (2^h-1) 个节点,这就是满二叉树。

完全二叉树:设二叉树的深度为 (h),除第 (h) 层外,其它各层的结点数都达到最大 个数,第 (h) 层所有的结点都连续集中在最左边,这就是完全二叉树。

分析
2018 pj t4,现在看这道题,不得不感叹,两年前的我是有多菜……
首先分析对称二叉树的特征,以便于我们判断对称二叉树。二叉树那条纯属废话,重点是,将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
考虑权值,首先对于一个根节点为(R)的树,如果他的左右节点相等,那么先递归一遍以这两个节点为根节点的左子树和右子树,再递归一遍以这两个节点为根节点的右子树和左子树。左右子树再次进行以上的操作,当两个节点都是-1,也就是都为叶子节点,return true;。但是如果在递归过程中发现u != v,不要怀疑,return false;,此时权值不对称。
上代码。
bool checkVal(int u, int v) {
if(u == -1 && v == -1) return true;
if(node[u].val == node[v].val && checkVal(node[u].l, node[v].r) && checkVal(node[u].r, node[v].l))
return true;
return false;
}
有趣的是,结构问题也顺带解决了。咋肥四?首先,如果结构不匹配,在递归过程中就会出现u == -1但v != -1的情况,或者是u != -1但v == -1的情况。这个时候,不满足第一个if,不满足第二个if,直接pass。
这种方法是不是很奇妙!
接下来是获得以每个节点为根节点的时候,这棵二叉树的大小。这个其实很好搞定,递归左右就完事。
void getSize(int u) {
if(node[u].l != -1) {
getSize(node[u].l);
node[u].size += node[node[u].l].size;
}
if(node[u].r != -1) {
getSize(node[u].r);
node[u].size += node[node[u].r].size;
}
}
在主函数中调用getSize(1),会自动算出所有节点的size。好棒棒!
让我想想还差什么,嗯,更新答案。更新答案这点在主函数中,我们需要遍历每一个节点,然后把这个节点的左右节点编号传给checkVal函数。如果checkVal函数判定这是一棵对称二叉树,那么就尝试更新ans。
其他的就没什么了,直接上代码吧~
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-03-09 22:53:04
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-03-10 00:04:03
*/
#include <iostream>
#include <cstdio>
const int maxn = 1000005;
int max(int a, int b) {
return a > b ? a : b;
}
struct Node {
int l;
int r;
int val;
int size;
}node[maxn];
void getSize(int u) {
if(node[u].l != -1) {
getSize(node[u].l);
node[u].size += node[node[u].l].size;
}
if(node[u].r != -1) {
getSize(node[u].r);
node[u].size += node[node[u].r].size;
}
}
bool checkVal(int u, int v) {
if(u == -1 && v == -1) return true;
if(node[u].val == node[v].val && checkVal(node[u].l, node[v].r) && checkVal(node[u].r, node[v].l))
return true;
return false;
}
int main() {
int n, ans = 0;
scanf("%d",&n);
for(int i = 1; i <= n; i++) {
scanf("%d", &node[i].val);
node[i].size = 1;
}
for(int i = 1; i <= n; i++)
scanf("%d%d", &node[i].l, &node[i].r);
getSize(1);
for(int i = 1; i <= n; i++)
if(checkVal(node[i].l, node[i].r))
ans = max(ans, node[i].size);
printf("%d
",ans);
return 0;
}
评测结果
AC 100:R31578398