数据集处理
数据获取
使用sklearn的dataset获取数据
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
iris_feature = iris['data']
iris_target = iris['target']
iris_target_name = iris['target_names']
数据划分
使用sklearn自带的函数将其分割为训练集和测试集
-
训练集和测试集比例为2:1
-
为方便比较不同方法的优劣,我们固定随机数种子为10
feature_train, feature_test, target_train, target_test = train_test_split(iris_feature, iris_target, test_size=0.33,random_state=10)
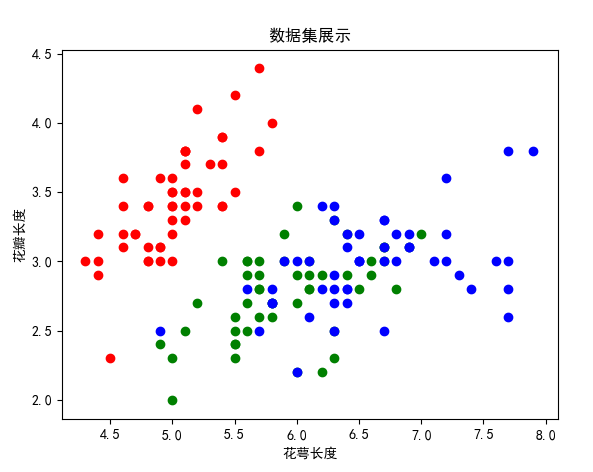
可视化
使用plt对数据进行可视化,数据集展示如下
def show():
t0 = [index for index in range(len(iris_target)) if iris_target[index] == 0]
t1 = [index for index in range(len(iris_target)) if iris_target[index] == 1]
t2 = [index for index in range(len(iris_target)) if iris_target[index] == 2]
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
# plt.rcParams['axes.unicode_minus'] = False
plt.scatter(x=iris_feature[t0, 0], y=iris_feature[t0, 1], color='r', label='Iris-virginica')
plt.scatter(x=iris_feature[t1, 0], y=iris_feature[t1, 1], color='g', label='Iris-setosa')
plt.scatter(x=iris_feature[t2, 0], y=iris_feature[t2, 1], color='b', label='Iris-versicolor')
plt.xlabel("花萼长度")
plt.ylabel("花瓣长度")
plt.title("数据集展示")
plt.show()
方法1 DecisionTree
类定义
为了构建决策树,需要先定义节点类
class Node:
def __init__(self, dimension, threshold, isLeaf, left, right, species):
self.dimension = dimension # 划分维度
self.threshold = threshold # 划分阈值
self.isLeaf = isLeaf # 是否是叶节点
self.left = left # 左支(叶节点时为None)
self.right = right # 右支(叶节点时为None)
self.species = species # 分类(如果是叶节点)
构建决策树
决策树部分,采用CART算法构建决策树,下面将按照依赖关系自底向上介绍结构化方法
基尼值
计算公式为
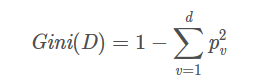
基尼值越小说明该数据集中不同类的数据越少
pv代表了v类数据在总类中的频率
代码实现如下
def get_gini(label):
"""
计算GINI值
:param label: 数组,里面存的是分类
:return: 返回Gini值
"""
gini = 1
dic = {}
for target in label:
if target in dic.keys():
dic[target] += 1
else:
dic[target] = 1
for value in dic.values():
tmp = value / len(label)
gini -= tmp * tmp
return gini
基尼系数
计算公式如下
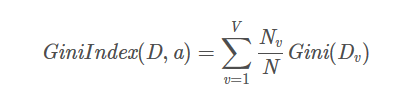
因为鸢尾花数据集的属性都是浮点数,为了二分化,我们需要寻找一个阈值,这里采用的方法是枚举所有的划分情况,因此需要做:
- 排序给定维度下的属性
- 选取相邻属性值的平均值作为候选阈值,并去重
- 遍历所有可能的阈值,选取基尼系数最小的划分阈值,返回基尼系数和划分阈值
代码实现如下
def get_gini_index_min(feature, label, dimension):
"""
获取某个维度的最小GiniIndex
:param feature: 所有属性list
:param label: 标记list
:param dimension: 维度(从0开始)
:return: gini_index(最小GiniIndex) threshold(对应阈值)
"""
attr = feature[:, dimension]
gini_index = 1
threshold = 0
attr_sort = sorted(attr)
candicate_thre = []
# 寻找候选阈值
for i in range(len(attr_sort) - 1):
tmp = (attr_sort[i] + attr_sort[i + 1]) / 2
if tmp not in candicate_thre:
candicate_thre.append(tmp)
# 寻找最小GiniIndex
for thre_tmp in candicate_thre:
index_small_list = [index for index in range(len(feature)) if attr[index] < thre_tmp]
label_small_tmp = label[index_small_list]
index_large_list = [index for index in range(len(feature)) if attr[index] >= thre_tmp]
label_large_tmp = label[index_large_list]
gini_index_tmp = get_gini(label_small_tmp) * len(label_small_tmp) / len(attr) + get_gini(label_large_tmp) * len(
label_large_tmp) / len(attr)
if gini_index_tmp < gini_index:
gini_index = gini_index_tmp
threshold = thre_tmp
print(gini_index, threshold)
return gini_index, threshold
寻找划分维度
鸢尾花数据集有四个维度的数据,我们需要确定选取哪个维度的数据作为划分依据,因此,我们依次计算各个维度下的最小基尼系数,选取最小基尼系数最小的维度作为划分维度
有了上面计算最小基尼系数的方法,我们可以来选取基尼系数最小的数据维度
def find_dimension_by_GiniIndex(feature, label):
"""
寻找划分维度
:param feature: 所有属性list
:param label: 标记list
:return: gini_index, threshold, dimension
"""
dimension = 0
threshold = 0
gini_index_min = 1
for d in range(len(feature[1])):
gini_index, thre = get_gini_index_min(feature, label, d)
if gini_index < gini_index_min:
gini_index_min = gini_index
dimension = d
threshold = thre
print(gini_index, threshold, dimension)
return gini_index, threshold, dimension
构建决策树
有了以上的工具,就用递归的方法构建决策树了
递归的终点有两种情况
- dataset只有一个元素了,那就不用再分了
- dataset里有很多元素,但都是同一类型的,体现在GiniIndex=0,说明已经纯洁,不用再递归
实现如下
def devide_by_dimension_and_thre(feature, label, threshold, dimension):
"""
根据阈值和维度来划分数据集,返回小集和大集
:param feature: 所有属性list
:param label: 标记list
:param threshold: 划分阈值
:param dimension: 划分维度
:return: feature_small, label_small, feature_large, label_large
"""
attr = feature[:, dimension]
index_small_list = [index for index in range(len(feature)) if attr[index] < threshold]
feature_small = feature[index_small_list]
label_small = label[index_small_list]
index_large_list = [index for index in range(len(feature)) if attr[index] >= threshold]
feature_large = feature[index_large_list]
label_large = label[index_large_list]
return feature_small, label_small, feature_large, label_large
def build_tree(feature, label):
"""
递归构建决策树
:param feature: 所有属性list
:param label: 标记list
:return: 决策树的根Node节点
"""
if len(label) > 1:
gini_index, threshold, dimension = find_dimension_by_GiniIndex(feature, label)
if gini_index == 0: # gini_index = 0,说明全都是同一种类型,就是叶节点
return Node(dimension, threshold, True, None, None, label[0])
print('end')
else:
# gini_index != 0,说明还不纯,继续划分,递归构建左支和右支
feature_small, label_small, feature_large, label_large = devide_by_dimension_and_thre(feature, label,
threshold,
dimension)
left = build_tree(feature_small, label_small)
right = build_tree(feature_large, label_large)
return Node(dimension, threshold, False, left, right, None)
else:
# 如果只有一个数据,直接是叶节点
return Node(None, None, True, None, None, label[0])
分类结果
使用graphviz对训练出的决策树进行可视化
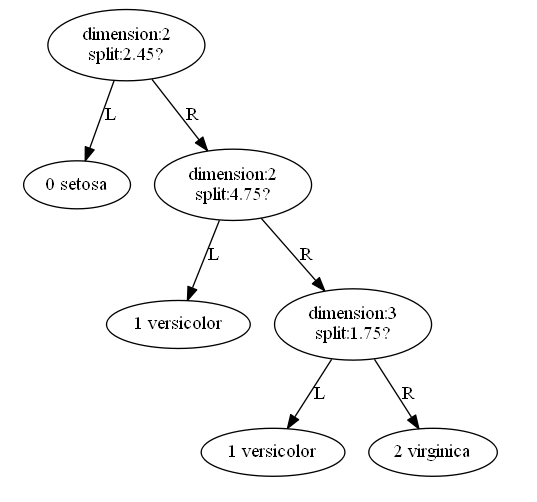
通过对测试集的预测来验证准确性
def predict(root: Node, feature_line):
"""
使用该方法进行预测
:param root: 决策树根节点
:param feature_line: 需要预测的属性值
:return: 预测结构 label
"""
node = root
while not node.isLeaf:
if feature_line[node.dimension] < node.threshold:
node = node.left
else:
node = node.right
return node.species
def score(root, feature, label):
"""
模型得分评估
:param root: 决策树根节点
:param feature: 测试集属性list
:param label: 测试集标记list
:return: 正确率
"""
correct = 0
for index in range(len(feature)):
type = predict(root, feature[index])
if type == label[index]:
correct += 1
print('correct rate is', correct / len(feature))
res = build_tree(feature_train, target_train)
score(res, feature_test, target_test)
得到正确率为0.96
经过验证,随机选取划分数据集的随机数种子(既按照2:1的训练集:测试集比例,随机划分),正确率都在90%以上,说明决策树方法能有效划分鸢尾花数据集
方法2 BPNN
BPNN(Back Propagation Neural Network)的主要思想是通过神经网络正向传播输出结果,通过反向传播(Back Propagation)方式传递误差,并对网络中的参数进行优化,以训练出一个神经网络。
这里直接通过构造一个BP神经网络,来实现对鸢尾花数据集分类例子,用代码来讲述对其的理解。
网络搭建
构建一个如图所示的神经网络
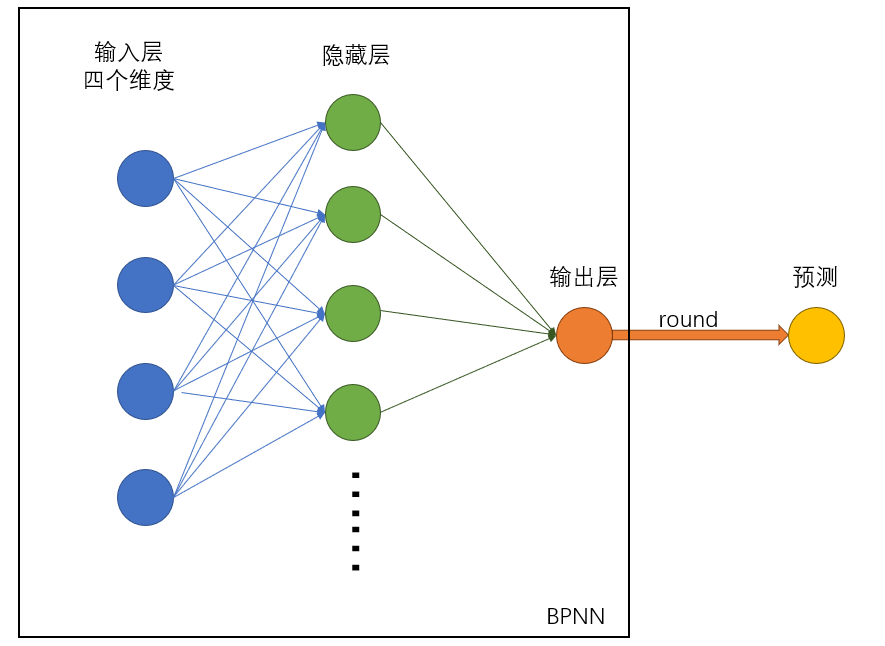
一些定义
- 输入层:input
- 隐藏层:hide
- 输出层:ouput
算法实现
初始化参数
类定义及初始化如下
class NeuralNetwork(object):
def __init__(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
"""
:param input_nodes: 输入层节点个数
:param hidden_nodes: 隐藏层节点个数
:param output_nodes: 输出层节点个数
:param learning_rate: 学习率
"""
self.input_nodes = input_nodes
self.hidden_nodes = hidden_nodes
self.output_nodes = output_nodes
self.weights_input_to_hidden = np.random.normal(0.0, self.hidden_nodes ** -0.5,
(self.hidden_nodes, self.input_nodes))
self.weights_hidden_to_output = np.random.normal(0.0, self.output_nodes ** -0.5,
(self.output_nodes, self.hidden_nodes))
self.lr = learning_rate # 学习率
self.activation_function = self.sigmoid
def sigmoid(self, x):
return 1.0 / (1 + np.exp(-x))
选择sigmoid函数作为激活函数
向前传播
向前传播指的已知各个节点的参数,如何得到神经网络的输出。
-
输入层inputs
-
隐藏层输入:通过输入层x权重得到隐藏层输入
hidden_inputs = np.dot(self.weights_input_to_hidden, inputs) -
隐藏层输出:通过隐藏层输入带入激活函数中获得
hidden_outputs = self.activation_function(hidden_inputs) -
结果层输入:通过隐藏层x权重得到结果层输入
final_inputs = np.dot(self.weights_hidden_to_output, hidden_outputs) -
结果层输出:尽管很多书上在这里会再使用一次激活函数,但因为期望的输出结果为分类target(0、1、2),而sigmoid函数的取值为(0,1),所以这里我们选择不再使用一次激活函数。结果证明这样处理下,仍然能够保持较好的准确率。
final_outputs = final_inputs
完整代码
def train(self, inputs_list, targets_list):
# 正向传播
inputs = np.array(inputs_list, ndmin=2).T
targets = np.array(targets_list, ndmin=2).T
hidden_inputs = np.dot(self.weights_input_to_hidden, inputs)
hidden_outputs = self.activation_function(hidden_inputs)
final_inputs = np.dot(self.weights_hidden_to_output, hidden_outputs)
final_outputs = final_inputs # 因为的取值为0、1、2,所以这里不再用激活函数了,否则结果会被限制在0到1
# 未完,见下
反向传播
反向传播主要是使用了梯度下降的方法来对参数进行修正,以提高拟合效果
(1)计算总误差
计算总的误差为:
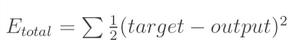
我们反向传播的目的就是对参数进行修正,使得Etotal达到最小。
(2)修正隐藏层-输出层参数
以权重weights_hidden_to_output[0]为例(为了表示方便记为w[0]),如果我们想知道他对总体误差产生了多少影响,可以对其求偏导。

同理,可以计算出所有的weights_hidden_to_output
代码实现如下
delta_output_out = final_outputs - targets
delta_output_in = delta_output_out
delta_weight_ho_out = np.dot(delta_output_in, hidden_outputs.T)
self.weights_hidden_to_output -= (self.lr * delta_weight_ho_out)
(3)修正输入层-隐藏层参数
这里需要先知道中间使用的激活函数sigmoid函数的求导
$$
sigmoid'(f(x))=f'(x)f(x)(1-f(x))
$$
以权重weights_input_to_hidden[0]为例(为了表示方便记为w[0]),如果我们想知道他对总体误差产生了多少影响,可以对其求偏导。

同理,可以计算出所有的weights_input_to_hidden
代码实现如下
delta_hidden_out = np.dot(self.weights_hidden_to_output.T, delta_output_in)
delta_hidden_in = delta_hidden_out * hidden_outputs * (1 - hidden_outputs)
delta_wih = np.dot(delta_hidden_in, inputs.T)
self.weights_input_to_hidden -= (self.lr * delta_wih)
关于正向传播、反向传播部分的参考
模型训练
epochs = 1000 # 训练次数
learning_rate = 0.001
hidden_nodes = 10
output_nodes = 1
batch_size = 50
input_nodes = train_features.shape[1]
network = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)
for e in range(epochs): # 进行epochs次训练
batch = np.random.choice(len(train_features), size=batch_size) # 从训练集中随机挑选50个样本进行训练
for record, target in zip(train_features[batch],
train_targets[batch]):
network.train(record, target)
分类结果
- 1000次训练下的损失函数图如下
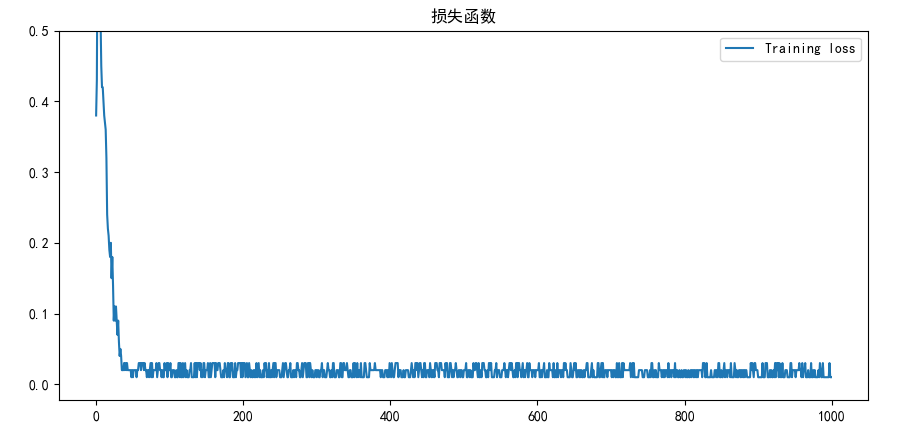
-
训练集的分类正确率为 0.98
测试集的分类正确率为 0.96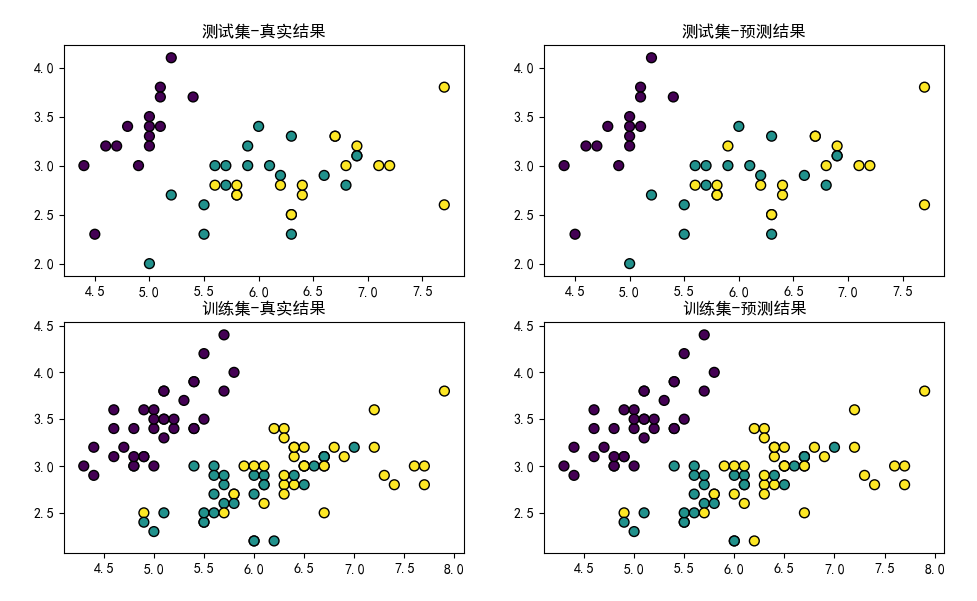
说明BPNN方法能有效划分鸢尾花数据集
方法3 SVM
理解
SVM
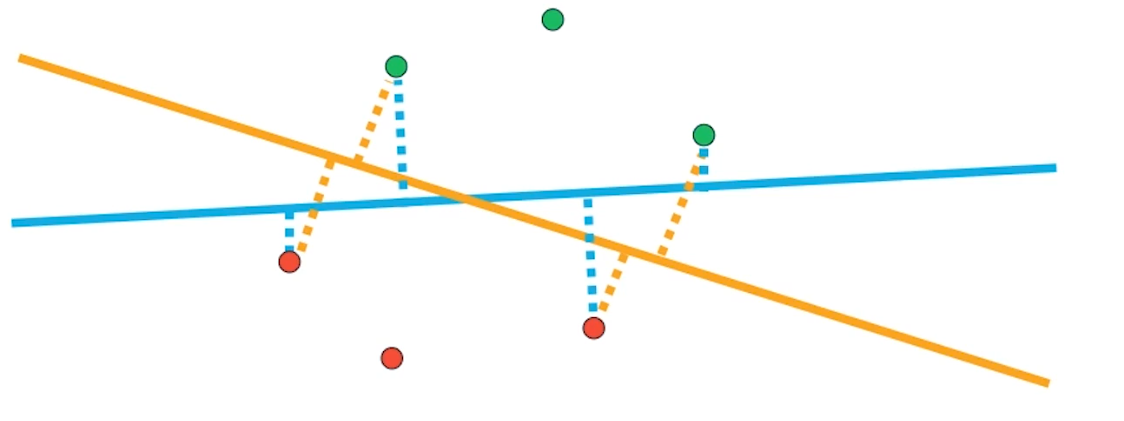
SVM是一种监督学习算法,主要思想是建立一个最优决策超平面,使得该平面两侧距平面最近的两类样本之间的距离最大化,从而对分类问题提供良好的泛化能力
以下图为例,黄色和蓝色是两种决策超平面,而黄色平面两侧距平面最近的两类样本之间的距离较大,所以可以称黄色是最优决策超平面。
而“支持向量”指训练集中的一些训练点,这些训练点最靠近决策面,是最难分类的数据点。比如图中画了虚线的四个点就是这种点。
寻找到这类超平面后,我们假设超平面方程为
$$
W^TX+b=0
$$
X为输入向量,W为权值向量,b为偏置,则可根据以下两个标准分为两类
$$
W^TX+b>0
$$
$$
W^TX+b<0
$$
核函数
为了划
分非线性数据,我们不能使用线性结果对其进行划分,如图,我们为了划分两类数据,没办法使用一条直线进行划分,而需要用曲线进行划分
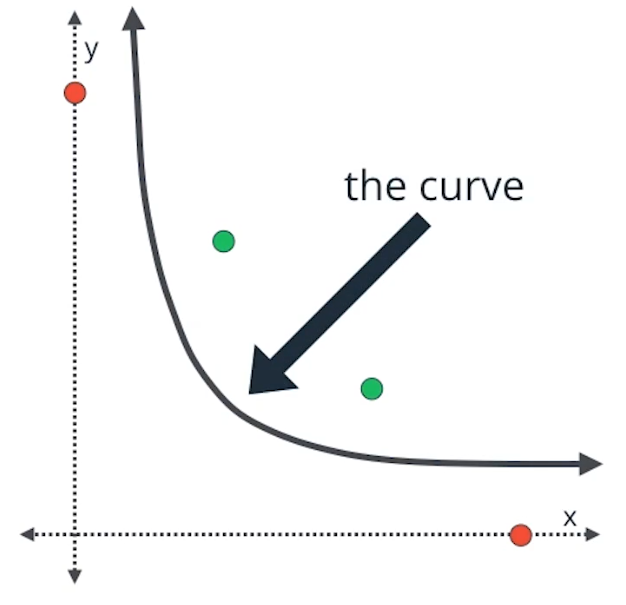
从高维的角度理解这个问题,原理是将数据映射到高维数据,在高维空间线性可分。
比如我们做一个从二维到三维的映射之后,就可以使用一个平面来划分这两类数据
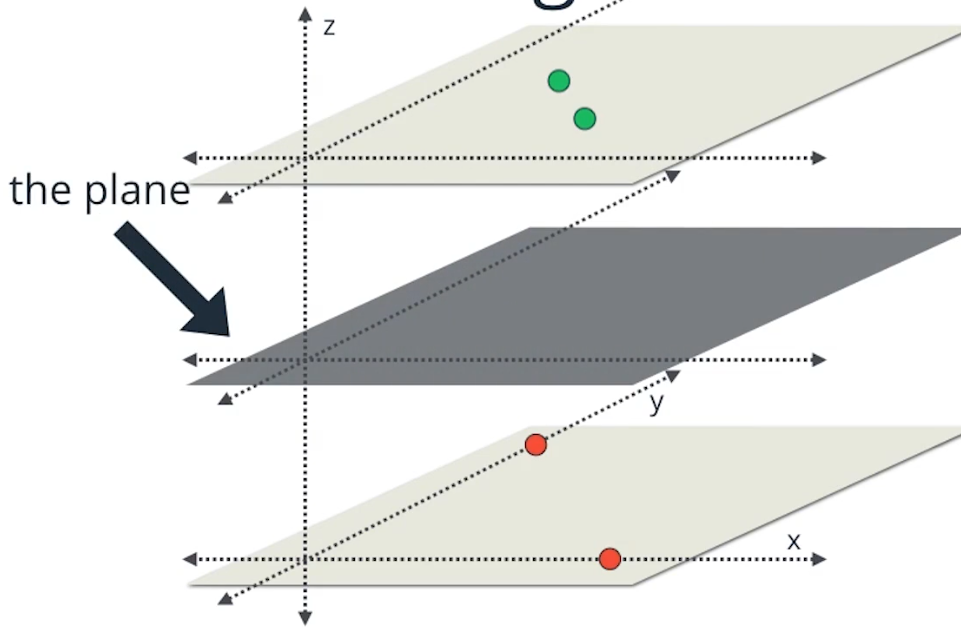
这种将原始空间中的向量作为输入向量,并返回特征空间(转换后的数据空间,可能是高维)中向量的点积的函数称为核函数。
一个来源网上的例子:

在下面的实现里,我们选用rbf作为核函数,径向基函数 (Radial Basis Function 简称 RBF),就是某种沿径向对称的标量函数,最常用的是高斯核函数。
高斯核本质是在衡量样本和样本之间的“相似度”,在一个刻画“相似度”的空间中,让同类样本更好的聚在一起,进而线性可分。
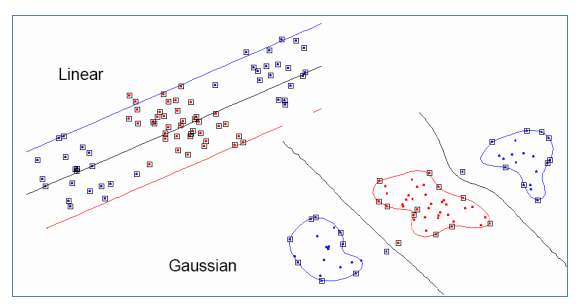
- 1,使用一个非线性映射将数据变换到一个特征空间 F
- 2,在特征空间使用线性学习器分类
实现
使用Sklearn自带的SVM模型进行实现
import matplotlib.pyplot as plt
from sklearn import svm
from data import feature_train, target_train, feature_test, target_test
svm_classifier = svm.SVC(C=1.0, kernel='rbf', decision_function_shape='ovr', gamma=0.01)
svm_classifier.fit(feature_train, target_train)
print("训练集:", svm_classifier.score(feature_train, target_train))
print("测试集:", svm_classifier.score(feature_test, target_test))
target_test_predict = svm_classifier.predict(feature_test)
comp = zip(target_test, target_test_predict)
print(list(comp))
plt.figure()
plt.subplot(121)
plt.scatter(feature_test[:, 0], feature_test[:, 1], c=target_test.reshape((-1)), edgecolors='k', s=50)
plt.subplot(122)
plt.scatter(feature_test[:, 0], feature_test[:, 1], c=target_test_predict.reshape((-1)), edgecolors='k', s=50)
plt.show()
分类结果如下
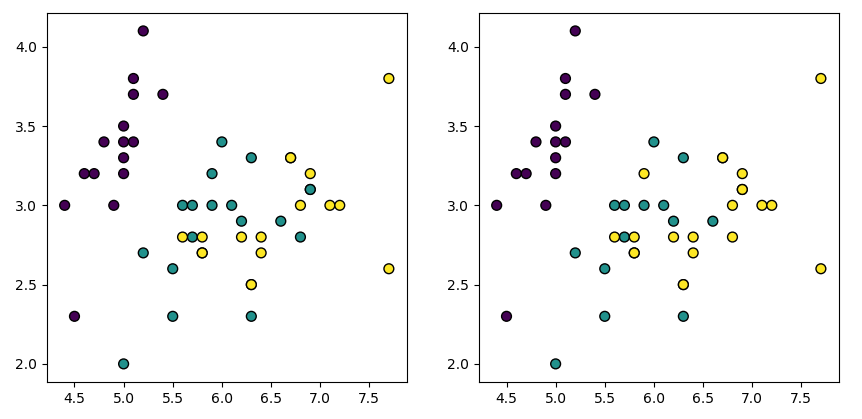
训练集的准确率: 0.95
测试集的准确率: 0.92
方法4 KNN
KNN分类器实现
距离计算
计算公式为
$$
d=sqrt{(x0-y0)2+(x1-y1)2+(x2-y2)2+(x3-y3)2}
$$
def get_distance(self, feature_line1, feature_line2):
tmp = 0
for i in range(len(feature_line1)):
tmp += (feature_line1[i] - feature_line2[i]) ** 2
return tmp ** 0.5
选择类型
直接选择距离最近的k-训练集中出现频率最高的种类作为分类结果
def get_type(self, k, feature_line):
dic = {}
for index in range(len(self.feature)):
dist = self.get_distance(self.feature[index], feature_line)
dic[index] = dist
# sort
sort_dic = sorted(dic.items(), key=lambda x: x[1], reverse=False)
# print(sort_dic)
vote = {}
for i in range(k):
index = sort_dic[i][0]
type = self.labels[index]
if type not in vote.keys():
vote[type] = 1
else:
vote[type] += 1
vote_rank = sorted(vote.items(), key=lambda x: x[1], reverse=True)
# print(vote_rank)
return vote_rank[0][0]
完整代码
class KNNClassifier:
def __init__(self, feature, labels):
self.feature = feature
self.labels = labels
def get_distance(self, feature_line1, feature_line2):
tmp = 0
for i in range(len(feature_line1)):
tmp += (feature_line1[i] - feature_line2[i]) ** 2
return tmp ** 0.5
def get_type(self, k, feature_line):
dic = {}
for index in range(len(self.feature)):
dist = self.get_distance(self.feature[index], feature_line)
dic[index] = dist
# sort
sort_dic = sorted(dic.items(), key=lambda x: x[1], reverse=False)
# print(sort_dic)
vote = {}
for i in range(k):
index = sort_dic[i][0]
type = self.labels[index]
if type not in vote.keys():
vote[type] = 1
else:
vote[type] += 1
vote_rank = sorted(vote.items(), key=lambda x: x[1], reverse=True)
# print(vote_rank)
return vote_rank[0][0]
def predict(self, k, feature):
res = []
for feature_line in feature:
res.append(self.get_type(k, feature_line))
return res
def score(self, k, feature, labels):
predict_set = self.predict(k, feature)
return len([index for index in range(len(labels)) if predict_set[index] == labels[index]]) / len(labels)
分类结果
选取k=5,训练结果如下:
训练集的准确率: 0.97
测试集的准确率: 0.96
使用plt绘制分布图:
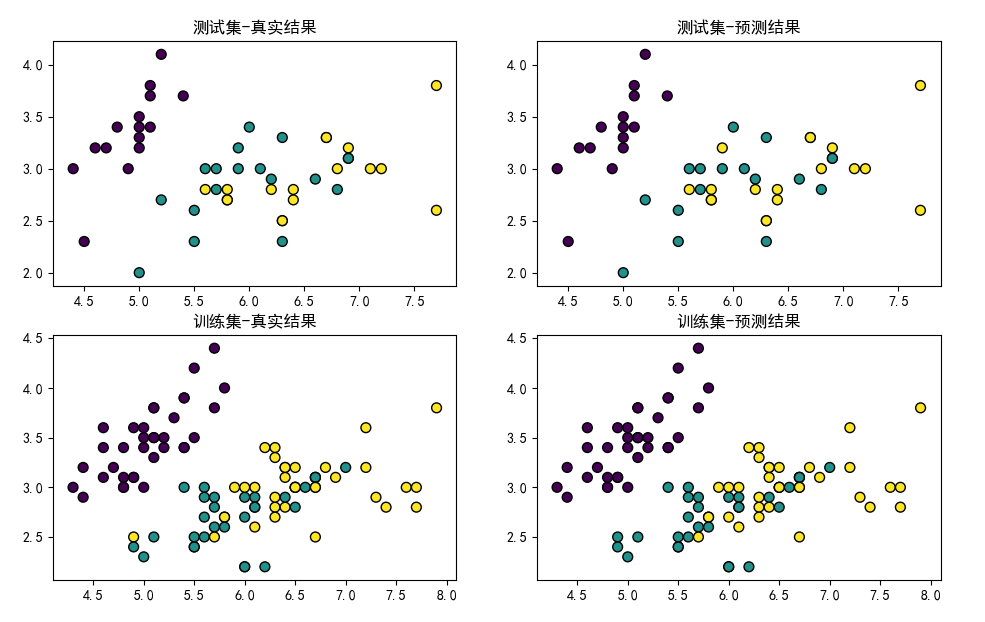
可以看出,KNN能够很好地对鸢尾花数据集进行分类