洛谷博客传送门
题意
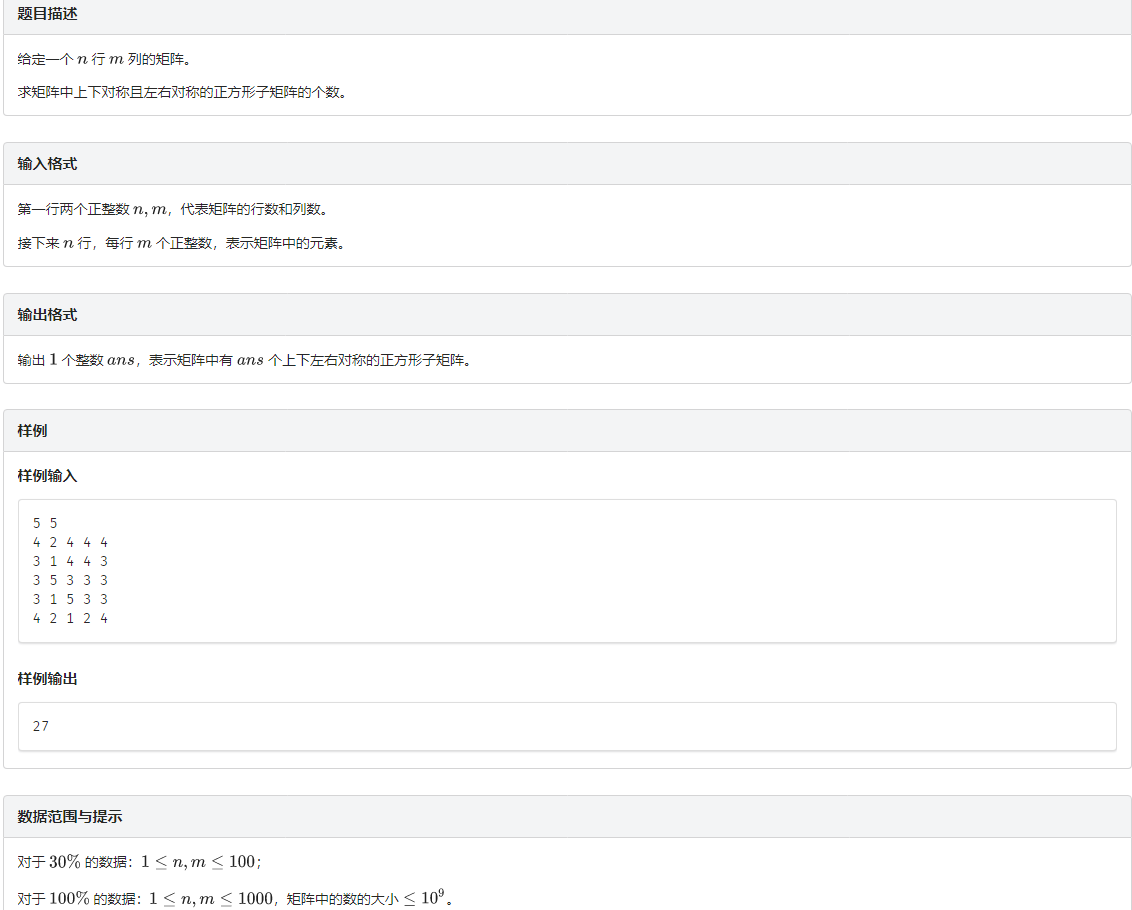
题解
这题洛谷上有,还是个紫题
根据对称的定义,再看看范围,容易想到二分答案(Hash好像经常和二分结合在一起)
二分部分
但是具体怎么二分?
首先确定,二分成立需要单调性,所以一定是从中心点二分,但是当正方形为奇数的时候中心点在中央的格子,那么偶数呢?
实际上,边长为偶数的时候正方形的重心在一个格点(就是一个点,不是格子)
概括一下:
- 对于长度为奇数的正方形,以格子(一个1*1的正方形)为中心二分最远符合条件的长度
- 对于长度为偶数的正方形,以格点(就是一个点)为中心二分最远符合条件的长度
那么二分的 check 函数就可以用二维Hash来O(1)判断
二维Hash部分
二维Hash的作用就是判断矩阵是否相同
就是横向和纵向分别算两次Hash值(base1,base2取不同的值),但是第二次Hash和第一次Hash略有不同,具体见代码
对于Hash值的查询,类似二维前缀和,下面贴的代码中 mi1,base1对应纵坐标 y ,mi2,base2对应横坐标 x,记住这个对应关系基本就不会写错
PS:这道题卡大部分模数1e9+7(0pts),1e9+9(20pts),98244353(0pts),然而用 ull 自然溢出就没事(100pts)
代码
最大子矩阵
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
const int INF = 0x3f3f3f3f,N = 1e3+10,base1 = 233,base2 = 133;
const ll mod = 1e9+9;
ull mi1[N<<1],mi2[N<<1],sum[N<<1][N<<1];
int len,a[N<<1][N<<1],n,m;
int ans;
void init()
{
mi1[0]=mi2[0]=1;
//这里所有的n,m不要忘记×2
for(int i=1;i<=m<<1;i++) mi1[i]=(mi1[i-1]*base1);
for(int i=1;i<=n<<1;i++) mi2[i]=(mi2[i-1]*base2);
for(int i=1;i<=n<<1;i++)
for(int j=1;j<=m<<1;j++)
sum[i][j]=sum[i][j-1]*base1+a[i][j];
for(int i=1;i<=n<<1;i++)
for(int j=1;j<=m<<1;j++)
sum[i][j]+=sum[i-1][j]*base2;//注意这里是+=
}
inline ll Hash(int xa,int ya,int xb,int yb)
{
return sum[xb][yb]-sum[xa-1][yb]*mi2[xb-xa+1]-
sum[xb][ya-1]*mi1[yb-ya+1]+
sum[xa-1][ya-1]*mi1[yb-ya+1]*mi2[xb-xa+1];
}
inline bool check(int xa,int ya,int xb,int yb)
{
return Hash(xa,ya,xb,yb)==Hash((n<<1)-xb+1,ya,(n<<1)-xa+1,yb)&&
Hash(xa,ya,xb,yb)==Hash(xa,(m<<1)-yb+1,xb,(m<<1)-ya+1);//+1要想好
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
a[i+n][j]=a[n-i+1][j];
a[i][j+m]=a[i][m-j+1];
}
init();//忘记调用init()还调了半天
// for(int i=1;i<=n<<1;i++)
// {
// for(int j=1;j<=m<<1;j++)
// printf("%lld ",sum[i][j]);
// puts("");
// }
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
//对于长度为奇数的正方形,以格子(一个1*1的正方形)为中心二分最远符合条件的长度
int l=0,r=max(n,m);
while(l<r)
{
int mid=(l+r+1)>>1;
if(i-mid>=1&&j-mid>=1&&i+mid<=n&&j+mid<=m&&check(i-mid,j-mid,i+mid,j+mid)) l=mid;
else r=mid-1;
}
//printf("#1:(%d,%d,%d,%d)
",i-l,j-l,i+l,j+l);
ans+=l+1;
//对于长度为偶数的正方形,以格点(就是一个点)为中心二分最远符合条件的长度
l=0,r=max(n,m);
while(l<r)
{
int mid=(l+r+1)>>1;
if(i-mid+1>=1&&j-mid+1>=1&&i+mid<=n&&j+mid<=m&&check(i-mid+1,j-mid+1,i+mid,j+mid)) l=mid;
else r=mid-1;
}
//printf("#2:(%d,%d,%d,%d)
",i-l+1,j-l+1,i+l,j+l);
ans+=l;
}
printf("%d
",ans);
return 0;
}