算法笔记 上机训练实战指南 第9章 提高篇(3)--数据结构专题(2) 学习笔记

9.2 二叉树的遍历

PAT A1020 Tree Traversals (25分)

Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder and inorder traversal sequences, you are supposed to output the level order traversal sequence of the corresponding binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤), the total number of nodes in the binary tree. The second line gives the postorder sequence and the third line gives the inorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the level order traversal sequence of the corresponding binary tree. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

Sample Output:

4 1 6 3 5 7 2

#include<cstdio>
#include<queue>
using namespace std;
int n;
const int maxn = 50;
int post[maxn],in[maxn];
struct node{
    int data;
    node* lchild;
    node* rchild;
};
node* create(int postL,int postR,int inL,int inR){
    if(postL > postR){
        return NULL;
    }
    node* root = new node;
    root->data = post[postR];
    int numleft,k;
    for(k=inL;k<=inR;k++){
        if(in[k] == post[postR]){
            break;
        }
    }
    numleft = k - inL;
    root->lchild = create(postL,postL+numleft-1,inL,k - 1);
    root->rchild = create(postL+numleft,postR-1,k + 1,inR);
    return root;
}
void BFS(node* root){
    queue<node*> q;
    q.push(root);
    int num = 0;
    while(!q.empty()){
        node* now = q.front();
        q.pop();
        printf("%d",now->data);
        num++;
        if(num < n){
            printf(" ");
        }
        if(now->lchild != NULL)
            q.push(now->lchild);
        if(now->rchild != NULL)
            q.push(now->rchild);
    }
}
int main(){
    scanf("%d",&n);
    for(int i = 0; i < n; i++){
        scanf("%d",&post[i]);
    }
    for(int i = 0; i < n; i++){
        scanf("%d",&in[i]);
    }
    node* root = create(0,n-1,0,n-1);
    BFS(root);
    return 0;
}

PAT A1086 Tree Traversals Again (25分)

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

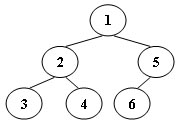
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2 lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

#include<cstdio>
#include<stack>
#include<cstring>
using namespace std;
const int maxn = 50;
int pre[maxn],in[maxn],post[maxn];
struct node{
    int data;
    node* lchild;
    node* rchild;
};
int n;
node* Create(int preL,int preR,int inL,int inR){
    if(preL > preR){
        return NULL;
    }
    node* root = new node;
    root->data = pre[preL];
    int k,numLeft;
    for(k = inL;k<=inR;k++){
        if(in[k] == pre[preL]){
            break;
        }
    }
    numLeft = k - inL;
    root->lchild = Create(preL+1,preL+numLeft,inL,k-1);
    root->rchild = Create(preL+numLeft+1,preR,k+1,inR);
    return root;
} 
int num =0;
void Posttraver(node* root){
    if(root == NULL){
        return;
    }
    Posttraver(root->lchild);
    Posttraver(root->rchild);
    printf("%d",root->data);
    num++;
    if(num < n){
        printf(" ");
    }
}
int main(){
    char str[5];
    scanf("%d",&n);
    int x,preIndex=0,inIndex=0;
    stack<int> st;
    for(int i=0;i< 2*n;i++){
        scanf("%s",str);
        if(strcmp(str,"Push")==0){
            scanf("%d",&x);
            pre[preIndex++] = x;
            st.push(x);
        }else{
            in[inIndex++] = st.top();
            st.pop();
        }
    }
    node* root = Create(0,n-1,0,n-1);
    Posttraver(root);
    return 0;
}

PAT A1079 Total Sales of Supply Chain (25分)

A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）-- everyone involved in moving a product from supplier to customer.

Starting from one root supplier, everyone on the chain buys products from one's supplier in a price P and sell or distribute them in a price that is r% higher than P. Only the retailers will face the customers. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.

Now given a supply chain, you are supposed to tell the total sales from all the retailers.

Input Specification:

Each input file contains one test case. For each case, the first line contains three positive numbers: N (≤), the total number of the members in the supply chain (and hence their ID's are numbered from 0 to N−1, and the root supplier's ID is 0); P, the unit price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then N lines follow, each describes a distributor or retailer in the following format:

K​i​​ ID[1] ID[2] ... ID[K​i​​]

where in the i-th line, K​i​​ is the total number of distributors or retailers who receive products from supplier i, and is then followed by the ID's of these distributors or retailers. K​j​​ being 0 means that the j-th member is a retailer, then instead the total amount of the product will be given after K​j​​. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the total sales we can expect from all the retailers, accurate up to 1 decimal place. It is guaranteed that the number will not exceed 1.

Sample Input:

10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0 7
2 6 1
1 8
0 9
0 4
0 3

Sample Output:

42.4

#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
int n;
double p,r,ans = 0;
const int maxn = 100010;
struct node{
    double data;
    vector<int> child;
}Node[maxn];
void DFS(int index,int depth){
    if(Node[index].child.size() == 0){
        ans += Node[index].data * pow(1 + r,depth);
        return;
    }
    for(int i=0;i < Node[index].child.size(); i++){
        DFS(Node[index].child[i],depth + 1);
    }
}
int main(){
    int k,child;
    scanf("%d%lf%lf",&n,&p,&r);
    r /= 100;
    for(int i=0;i<n;i++){
        scanf("%d",&k);
        if(k == 0){
            scanf("%lf",&Node[i].data);
        }else{
            for(int j=0;j<k;j++){
                scanf("%d",&child);
                Node[i].child.push_back(child);
            }
        }    
    }
    DFS(0,0);
    printf("%.1f
",p * ans);
    return 0;
}

PAT A1090 Highest Price in Supply Chain (25分)

A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）-- everyone involved in moving a product from supplier to customer.

Starting from one root supplier, everyone on the chain buys products from one's supplier in a price P and sell or distribute them in a price that is r% higher than P. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.

Now given a supply chain, you are supposed to tell the highest price we can expect from some retailers.

Input Specification:

Each input file contains one test case. For each case, The first line contains three positive numbers: N (≤), the total number of the members in the supply chain (and hence they are numbered from 0 to N−1); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then the next line contains N numbers, each number S​i​​ is the index of the supplier for the i-th member. S​root​​ for the root supplier is defined to be −. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the highest price we can expect from some retailers, accurate up to 2 decimal places, and the number of retailers that sell at the highest price. There must be one space between the two numbers. It is guaranteed that the price will not exceed 1.

Sample Input:

9 1.80 1.00
1 5 4 4 -1 4 5 3 6

Sample Output:

1.85 2

#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
const int maxn = 100010;
int n,maxdepth = 0, num = 0;
double p,r;
vector<int> child[maxn];
void DFS(int index,int depth){
    if(child[index].size() == 0){
        if(depth > maxdepth){
            maxdepth = depth;
            num = 1;
        }else if(depth == maxdepth){
            num++;
        }
        return;
    }
    for(int i= 0;i<child[index].size();i++){
        DFS(child[index][i],depth+1);
    }
    
}
int main(){
    int father,root;
    scanf("%d%lf%lf",&n,&p,&r);
    r /= 100;
    for(int i=0;i<n;i++){
        scanf("%d",&father);
        if(father != -1){
            child[father].push_back(i);
        }else{
            root = i;
        }
    }
    DFS(root,0);
    printf("%.2f %d",p*pow(1+r,maxdepth),num);
    return 0;
}

PAT A1094 The Largest Generation (25分)

A family hierarchy is usually presented by a pedigree tree where all the nodes on the same level belong to the same generation. Your task is to find the generation with the largest population.

Input Specification:

Each input file contains one test case. Each case starts with two positive integers N (<) which is the total number of family members in the tree (and hence assume that all the members are numbered from 01 to N), and M (<) which is the number of family members who have children. Then M lines follow, each contains the information of a family member in the following format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a family member, K (>) is the number of his/her children, followed by a sequence of two-digit ID's of his/her children. For the sake of simplicity, let us fix the root ID to be 01. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the largest population number and the level of the corresponding generation. It is assumed that such a generation is unique, and the root level is defined to be 1.

Sample Input:

23 13
21 1 23
01 4 03 02 04 05
03 3 06 07 08
06 2 12 13
13 1 21
08 2 15 16
02 2 09 10
11 2 19 20
17 1 22
05 1 11
07 1 14
09 1 17
10 1 18

Sample Output:

9 4

#include<cstdio>
#include<vector>
using namespace std;
const int maxn = 110;
vector<int> Node[maxn];
int hashTable[maxn] = {0};
void DFS(int index,int level){
    hashTable[level]++;
    for(int i=0;i<Node[index].size();i++){
        DFS(Node[index][i],level + 1);
    }
}
int main(){
    int n,m,parent,k,child;
    scanf("%d%d",&n,&m);
    for(int i = 0;i < m;i++){
        scanf("%d%d",&parent,&k);
        for(int j = 0; j < k;j++){
            scanf("%d",&child);
            Node[parent].push_back(child);
        }
    }
    DFS(1,1);
    int maxLevel = -1,maxValue = 0;
    for(int i = 1;i<maxn;i++){
        if(hashTable[i] > maxValue){
            maxValue = hashTable[i];
            maxLevel = i;
        }
    }
    printf("%d %d
",maxValue,maxLevel);
    return 0;
}

PAT A1106 Lowest Price in Supply Chain (25分)

A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）-- everyone involved in moving a product from supplier to customer.

Starting from one root supplier, everyone on the chain buys products from one's supplier in a price P and sell or distribute them in a price that is r% higher than P. Only the retailers will face the customers. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.

Now given a supply chain, you are supposed to tell the lowest price a customer can expect from some retailers.

Input Specification:

Each input file contains one test case. For each case, The first line contains three positive numbers: N (≤), the total number of the members in the supply chain (and hence their ID's are numbered from 0 to N−1, and the root supplier's ID is 0); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then N lines follow, each describes a distributor or retailer in the following format:

K​i​​ ID[1] ID[2] ... ID[K​i​​]

where in the i-th line, K​i​​ is the total number of distributors or retailers who receive products from supplier i, and is then followed by the ID's of these distributors or retailers. K​j​​ being 0 means that the j-th member is a retailer. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in one line the lowest price we can expect from some retailers, accurate up to 4 decimal places, and the number of retailers that sell at the lowest price. There must be one space between the two numbers. It is guaranteed that the all the prices will not exceed 1.

Sample Input:

10 1.80 1.00
3 2 3 5
1 9
1 4
1 7
0
2 6 1
1 8
0
0
0

Sample Output:

1.8362 2

#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
int n,num = 0;
const int maxn = 100010;
const double INF = 1e12;
vector<int> Node[maxn];
double p,r,ans = INF;
void DFS(int index,int depth){
    if(Node[index].size() == 0){
        double price = p * pow(1+r,depth);
        if(price < ans){
            ans = price;
            num = 1;
        }else if(price == ans){
            num++;
        }
        return;
    }
    for(int i = 0;i<Node[index].size();i++){
        DFS(Node[index][i],depth+1);
    }
}
int main(){
    int k,child;
    scanf("%d%lf%lf",&n,&p,&r);
    r /= 100;
    for(int i=0;i<n;i++){
        scanf("%d",&k);
        for(int j=0;j<k;j++){
            scanf("%d",&child);
            Node[i].push_back(child);
        }
    }
    DFS(0,0);
    printf("%.4f %d",ans,num);
    return 0;
}

PAT A1004 Counting Leaves (30分)

A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0, the number of nodes in a tree, and M (<), the number of non-leaf nodes. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 01.

The input ends with N being 0. That case must NOT be processed.

Output Specification:

For each test case, you are supposed to count those family members who have no child for every seniority level starting from the root. The numbers must be printed in a line, separated by a space, and there must be no extra space at the end of each line.

The sample case represents a tree with only 2 nodes, where 01 is the root and 02 is its only child. Hence on the root 01 level, there is 0 leaf node; and on the next level, there is 1 leaf node. Then we should output 0 1 in a line.

Sample Input:

2 1
01 1 02

Sample Output:

0 1

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int n,m;
const int maxn = 110;
vector<int> G[maxn];
int leaf[maxn] = {0};
int max_h = 1;
void DFS(int index,int h){
    max_h = max(h,max_h);
    if(G[index].size() == 0){
        leaf[h]++;
        return;
    }
    for(int i = 0;i < G[index].size();i++){
        DFS(G[index][i],h+1); 
    }
}
int main(){
    int child,parent,k;
    scanf("%d%d",&n,&m);
    for(int i=0;i<m;i++){
        scanf("%d%d",&parent,&k);
        for(int j = 0;j<k;j++){
            scanf("%d",&child);
            G[parent].push_back(child);
        }
    }
    DFS(1,1);
    printf("%d",leaf[1]);
    for(int i=2;i<=max_h;i++)
        printf(" %d",leaf[i]);
    return 0;
}

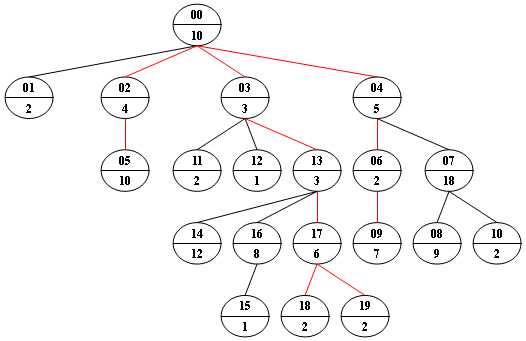
PAT A1053 Path of Equal Weight (30分)

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0, the number of nodes in a tree, M (<), the number of non-leaf nodes, and 0, the given weight number. The next line contains N positive numbers where W​i​​ (<) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence { is said to be greater than sequence { if there exists 1 such that A​i​​=B​i​​ for ,, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

10 5 2 7
10 4 10
10 3 3 6 2
10 3 3 6 2

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 110;
struct node{
    int weight;
    vector<int> child;
}Node[MAXN];
int n,m,s;
int path[MAXN];
bool cmp(int a,int b){
    return Node[a].weight > Node[b].weight;
}
void DFS(int index,int numNode,int sum){
    if(sum > s)
        return;
    if(sum == s){
        if(Node[index].child.size() != 0)
            return;
        for(int i = 0;i<numNode;i++){
            printf("%d",Node[path[i]].weight);
            if(i < numNode - 1)
                printf(" ");
            else
                printf("
");
        }
        return;
    }
    for(int i=0;i<Node[index].child.size();i++){
        int child = Node[index].child[i];
        path[numNode] = child;
        DFS(child,numNode+1,sum+Node[child].weight);
    }
}
int main(){
    int weight,parent,child,k;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=0;i<n;i++){
        scanf("%d",&weight);
        Node[i].weight = weight;
    }
    for(int i=0;i<m;i++){
        scanf("%d%d",&parent,&k);
        for(int j=0;j<k;j++){
            scanf("%d",&child);
            Node[parent].child.push_back(child);
        }
        sort(Node[parent].child.begin(),Node[parent].child.end(),cmp);
    }
    path[0] = 0;
    DFS(0,1,Node[0].weight);
    return 0;
}

9.4 二叉查找树(BST)

PAT A1043 Is It a Binary Search Tree (25分)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

If we swap the left and right subtrees of every node, then the resulting tree is called the Mirror Image of a BST.

Now given a sequence of integer keys, you are supposed to tell if it is the preorder traversal sequence of a BST or the mirror image of a BST.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤). Then N integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, first print in a line YES if the sequence is the preorder traversal sequence of a BST or the mirror image of a BST, or NO if not. Then if the answer is YES, print in the next line the postorder traversal sequence of that tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

Sample Input 1:

7
8 6 5 7 10 8 11

Sample Output 1:

YES
5 7 6 8 11 10 8

Sample Input 2:

7
8 10 11 8 6 7 5

Sample Output 2:

YES
11 8 10 7 5 6 8

Sample Input 3:

7
8 6 8 5 10 9 11

Sample Output 3:

NO

#include<cstdio>
#include<vector>
using namespace std;
vector<int> origin,pre,preM,post,postM;
struct node{
    int data;
    node *left,*right;
};
void insert(node* &root,int data){
    if(root == NULL){
        root = new node;
        root->data = data;
        root->left = root->right = NULL;
        return;
    }
    if(root->data > data){
        insert(root->left,data);
    }else{
        insert(root->right,data);
    }
}
void preOrder(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    vi.push_back(root->data);
    preOrder(root->left,vi);
    preOrder(root->right,vi);
}
void preOrderMirror(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    vi.push_back(root->data);
    preOrderMirror(root->right,vi);
    preOrderMirror(root->left,vi);
}
void postOrder(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    postOrder(root->left,vi);
    postOrder(root->right,vi);
    vi.push_back(root->data);
}
void postOrderMirror(node* root,vector<int> &vi){
    if(root == NULL)
        return;
    postOrderMirror(root->right,vi);
    postOrderMirror(root->left,vi);
    vi.push_back(root->data);
}
int main(){
    int n,data;
    scanf("%d",&n);
    node* root = NULL;
    for(int i=0;i<n;i++){
        scanf("%d",&data);
        origin.push_back(data);
        insert(root,data);
    }
    preOrder(root,pre);
    preOrderMirror(root,preM);
    postOrder(root,post);
    postOrderMirror(root,postM);
    if(origin == pre){
        printf("YES
");
        for(int i=0;i<post.size();i++){
            printf("%d",post[i]);
            if(i < post.size() - 1)
                printf(" ");
        }
    }else if(origin == preM){
        printf("YES
");
        for(int i = 0;i < postM.size();i++){
            printf("%d",postM[i]);
            if(i < postM.size()-1)
                printf(" ");
        }
    }else{
        printf("NO
");
    }
    return 0;
}

PAT A1064 Complete Binary Search Tree (30分)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

A Complete Binary Tree (CBT) is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.

Now given a sequence of distinct non-negative integer keys, a unique BST can be constructed if it is required that the tree must also be a CBT. You are supposed to output the level order traversal sequence of this BST.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤). Then N distinct non-negative integer keys are given in the next line. All the numbers in a line are separated by a space and are no greater than 2000.

Output Specification:

For each test case, print in one line the level order traversal sequence of the corresponding complete binary search tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line.

Sample Input:

10
1 2 3 4 5 6 7 8 9 0

Sample Output:

6 3 8 1 5 7 9 0 2 4

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 1010;
int n;
int number[MAXN],CBT[MAXN],index = 0;
void inorder(int root){
    if(root > n)
        return;
    inorder(root * 2);
    CBT[root] = number[index++];
    inorder(root * 2 +1);
}
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&number[i]);
    }    
    sort(number,number+n);
    inorder(1);
    for(int i=1;i<=n;i++){
        printf("%d",CBT[i]);
        if(i < n)
            printf(" ");
    }
    return 0;
}

PAT A1099 Build A Binary Search Tree (30分)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node's key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node's key.
• Both the left and right subtrees must also be binary search trees.

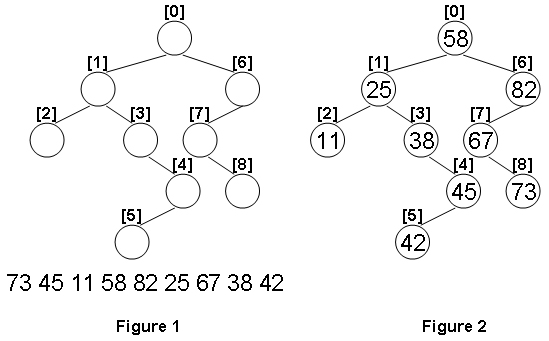
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then − will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification:

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input:

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output:

58 25 82 11 38 67 45 73 42

#include<cstdio>
#include<queue>
#include<algorithm>
using namespace std;
const int MAXN = 110;
struct node{
    int data;
    int lchild,rchild;
}Node[MAXN];
int n,in[MAXN],num = 0;
void inOrder(int root){
    if(root == -1)
        return;
    inOrder(Node[root].lchild);
    Node[root].data = in[num++];
    inOrder(Node[root].rchild);
}
void BFS(int root){
    queue<int> q;
    q.push(root);
    num = 0;
    while(!q.empty()){
        int now = q.front();
        q.pop();
        printf("%d",Node[now].data);
        num++;
        if(num < n)
            printf(" ");
        if(Node[now].lchild != -1)
            q.push(Node[now].lchild);
        if(Node[now].rchild != -1)
            q.push(Node[now].rchild);
    }
}
int main(){
    int lchild,rchild;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d%d",&lchild,&rchild);
        Node[i].lchild = lchild;
        Node[i].rchild = rchild;
    }
    for(int i=0;i<n;i++){
        scanf("%d",&in[i]);
    }
    sort(in,in+n);
    inOrder(0);
    BFS(0);
    return 0;
}

PAT A1066 Root of AVL Tree (25分)

 

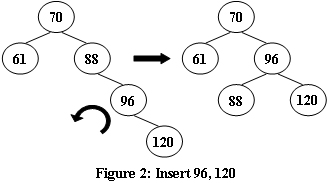
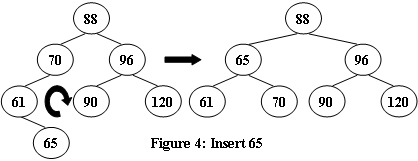
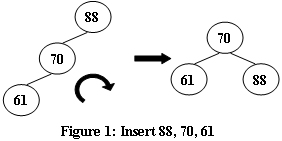
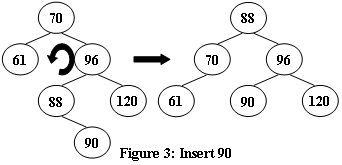
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

  

 

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

#include<cstdio>
#include<algorithm>
using namespace std;
struct node{
    int v,height;
    node *lchild,*rchild;
}*root;
//生成一个新结点，v为结点权值
node* newNode(int v){
    node* Node = new node;    //申请一个node型变量的地址空间 
    Node->v = v;    //结点权值为v 
    Node->height = 1;    //结点高度初始为1 
    Node->lchild = Node->rchild = NULL;    //初始状态下没有左右孩子 
    return Node;    //返回新建结点的地址 
} 
//获取以root为根结点的子树的当前height
int getHeight(node* root){
    if(root == NULL)
        return 0;
    return root->height;
} 
//更新结点root的height
void updateHeight(node* root){
    //max(左孩子的height,右孩子的height) + 1
    root->height = max(getHeight(root->lchild),getHeight(root->rchild)) + 1;
} 
//计算结点root的平衡因子
int getBalanceFactor(node* root){
    //左子树高度减右子树高度
    return getHeight(root->lchild) - getHeight(root->rchild); 
} 
//左旋
void L(node* &root){
    node* temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
} 
//右旋
void R(node* &root){
    node* temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
} 
//插入权值为v的结点 
void insert(node* &root,int v){
    if(root == NULL){ //到达空结点 
        root = newNode(v); 
        return; 
    }
    if(v < root->v){
        insert(root->lchild,v);
        updateHeight(root);
        if(getBalanceFactor(root) == 2){
            if(getBalanceFactor(root->lchild) == 1){
                R(root);
            }else if(getBalanceFactor(root->lchild) == -1){
                L(root->lchild);
                R(root);
            }
        }    
    }else{
        insert(root->rchild,v);
        updateHeight(root);
        if(getBalanceFactor(root) == -2){
            if(getBalanceFactor(root->rchild) == -1){
                L(root);
            }else if(getBalanceFactor(root->rchild) == 1){
                R(root->rchild);
                L(root);
            }
        }
    } 
} 
//AVL树的建立
node* Create(int data[],int n){
    node* root = NULL;
    for(int i=0;i<n;i++){
        insert(root,data[i]);
    }
    return root;
} 
int main(){
    int n,v;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&v);
        insert(root,v);
    }
    printf("%d
",root->v);
    return 0;
}

9.6 并查集

PAT A1107 Social Clusters (30分)

When register on a social network, you are always asked to specify your hobbies in order to find some potential friends with the same hobbies. A social cluster is a set of people who have some of their hobbies in common. You are supposed to find all the clusters.

Input Specification:

Each input file contains one test case. For each test case, the first line contains a positive integer N (≤), the total number of people in a social network. Hence the people are numbered from 1 to N. Then N lines follow, each gives the hobby list of a person in the format:

K​i​​: h​i​​[1] h​i​​[2] ... h​i​​[K​i​​]

where K​i​​ (>) is the number of hobbies, and [ is the index of the j-th hobby, which is an integer in [1, 1000].

Output Specification:

For each case, print in one line the total number of clusters in the network. Then in the second line, print the numbers of people in the clusters in non-increasing order. The numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
3: 2 7 10
1: 4
2: 5 3
1: 4
1: 3
1: 4
4: 6 8 1 5
1: 4

Sample Output:

3
4 3 1

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1010;
int father[maxn];
int isRoot[maxn]={0};
int course[maxn]={0};
bool cmp(int a,int b){
    return a > b;
}
void init(int n){
    for(int i=1;i<=n;i++){
        father[i] = i;
        isRoot[i] = 0;
    }
}
int findFather(int x){
    int a = x;
    while(x != father[x]){
        x = father[x];
    }
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
} 
void Union(int a,int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB)
        father[faA] = faB;
}
int main(){
    int n,k,h;
    scanf("%d",&n);
    init(n);
    for(int i = 1;i <= n;i++){
        scanf("%d:",&k);
        for(int j=0;j<k;j++){
            scanf("%d",&h);
            if(course[h] == 0){
                course[h] = i;
            }
            Union(i,course[h]);    
        }
    }
    int ans = 0;
    for(int i=1;i<=n;i++){
        isRoot[findFather(i)]++;
    }
    for(int i = 1;i<=n;i++){
        if(isRoot[i] != 0){
            ans++;
        }
    }
    printf("%d
",ans);
    sort(isRoot+1,isRoot+1+n,cmp);
    for(int i=1;i<=ans;i++){
        printf("%d",isRoot[i]);
        if(i < ans)
            printf(" ");
    }
    return 0;
}