DDA与Bresenham画线算法

一、数字微分分析仪（digital differential analyzer, DDA）方法是一种线段扫描转换算法。在一个坐标轴上以单位间隔对线段取样，从而确定另一个坐标轴上最靠近线路径的对应整数值。主要是根据直线公式y = kx + b来推导出来的，其关键之处在于如何设定单位步进，即一个方向的步进为单位步进，另一个方向的步进必然是小于1。

算法过程：

输入线段两个端点的像素位置，端点位置间的水平和垂直差赋给参数dx和dy。绝对值大的参数确定steps的值。从像素位置（xBegin，yBegin）开始，确定沿线段生成下一个像素位置的每一步所需的偏移量，并循环上述过程setps次。假如dx的绝对值大于dy的绝对值，且xBegin小于xEnd，那么x和y方向的增量值分别为1和m。假如x方向的变化较大，但xBegin大于xEnd，那么就采用减量-1和-m来生成线段上的每个点。在其他情况下，y方向使用单位增量（或减量），x方向使用1/m的增量（或减量）。

 1 inline int Round(const float a) { return static_cast<int>(a + 0.5); }
 2 
 3 void LineDDA(int xBegin, int yBegin, int xEnd, int yEnd)
 4 {
 5     int dx = xEnd - xBegin;
 6     int dy = yEnd - yBegin;
 7     int steps, k;
 8 
 9     float xIncrement, yIncrement;
10     float x = static_cast<int>(xBegin);
11     float y = static_cast<int>(yBegin);
12 
13     if (fabs(dx) > fabs(dy)) {
14         steps = fabs(dx);
15     }
16     else {
17         steps = fabs(dy);
18     }
19 
20     xIncrement = static_cast<float>(dx) / static_cast<float>(steps);
21     yIncrement = static_cast<float>(dy) / static_cast<float>(steps);
22 
23     glBegin(GL_POINTS);
24 
25     for (k = 0; k < steps; ++k) {
26         x += xIncrement;
27         y += yIncrement;
28         glVertex2i(round(x), round(y));
29     }
30     glEnd();
31 }

二、Bresenham画线算法是一种精确而有效的光栅线生成算法，该算法仅仅使用了增量整数计算。

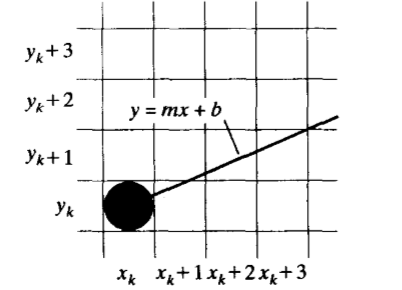
在取样位置 $x_{k}+1$ ，用 $d_{lower}$ 和 $d_{upper}$ 来标识两个像素与数学上线路径的垂直偏移。在像素列位置 $x_{k}+1$ 处的直线上的 $y$ 坐标可计算为

$y=m(x_{k}+1)+b$

那么

$d_{lower}=y-y_{k}=m(x_{k}+1)+b-y_{k}$

和

$d_{upper}=(y_{k}+1)-y=y_{k}+1-m(x_{k}+1)-b$

要确定两像素中哪一个更接近线路径，需测试两个像素偏移的差：

$d_{lower}-d_{upper}=2m(x_{k}+1)-2y_{k}+2b-1$

令 $m=\Delta y/\Delta x$

$p_{k}=\Delta x(d_{lower}-d_{upper})=2\Delta y\cdot x_{k}-2\Delta x\cdot y_{k}+c$

则 $p_{k+1}=2\Delta y\cdot x_{k+1}-2\Delta x\cdot y_{k+1}+c$

相减可得到

$p_{k+1}-p_{k}=2\Delta y(x_{k+1}-x_{k})-2\Delta x(y_{k+1}-y_{k})$

因 $x_{k+1}=x_{k}+1$

$p_{k+1}-p_{k}=2\Delta y-2\Delta x(y_{k+1}-y_{k})$ 　　　

算法过程：

$\left | m \right |<1$ 时的Bresenham画线算法：

1.输入线段的两个端点，并将左端点存储在(xBegin, yBegin)中；

2.将(xBegin, yBegin)装入帧缓存，画出第一个点；

3.计算常量 $\Delta x$ 、 $\Delta y$ 、 $2\Delta y$ 和 $2\cdot (\Delta y-\Delta x)$ ，并得到决策参数的第一个值：

$p_{0}=2\Delta y-\Delta x$

4.从 $k=0$ 开始，在沿线路径的每个 $x_{k}$ 处，进行下列检测：

如果 $p_{k}<0$ ，下一个要绘制的点是 $(x_{k+1},y_{k})$ ，并且

$p_{k+1}=p_{k}+2\Delta y$

否则，下一个要绘制的点是 $(x_{k+1},y_{k+1})$ ，并且

$p_{k+1}=p_{k}+2\Delta y-2\Delta x$

5.重读步骤4，共次 $\Delta x-1$ ;

 1 void LineBresenham(int xBegin, int yBegin, int xEnd, int yEnd)
 2 {
 3     int dx = fabs(xEnd - xBegin);
 4     int dy = fabs(yEnd - yBegin);
 5 
 6 
 7     int p = 2 * dy - dx;
 8     int two_dy = 2 * dy;
 9     int two_dy_minus_dx = 2 * (dy - dx);
10     int x, y;
11     int yName;
12 
13     if (xBegin > xEnd) {
14         yName = yBegin - yEnd;
15         x = xEnd;
16         y = yEnd;
17         xEnd = xBegin;
18     }
19     else {
20         yName = yEnd - yBegin;
21         x = xBegin;
22         y = yBegin;
23     }
24     while (x <= xEnd) {
25         glBegin(GL_POINTS);
26         glVertex2i(x, y);
27         glEnd();
28         
29         if (dx == 0 && y < yEnd) {
30             y++;
31             continue;
32         }
33         if (p < 0) {
34             x++;
35             p += two_dy;
36         }
37         else if (yName > 0) {
38             y++;
39             x++;
40             p += two_dy_minus_dx;
41         }
42         else if (yName < 0) {
43             y--;
44             x++;
45             p += two_dy_minus_dx;
46         }
47     }
48 }

相关阅读:
TestNG+maven+idea 环境基本使用
 linux基本命令
 linux -查看cpu 内存磁盘端口进程
 Scanner类、Random类、ArrayList 类
 （四）面向对象
 （三）数组
 （二）流程-循环
 （一）java基础_常量+变量+数据类型+运算符+方法
 SQL （二）
SQL（一）
原文地址：https://www.cnblogs.com/clairvoyant/p/5523429.html