Preface
感觉最近有点怠惰,都不是很想写代码
一定要坚持啊,不能天天颓废了虽然棋瘾还是很重的说
先把Div2写了吧,如果感觉海星可能会去打一下Div1
A. Difference Operations
从前往后考虑每一个数,如果这个数不能被删成零,那么后面的操作也影响不了它了,一定无解
如果可以被删成零,考虑先保留一点给后面的删,那么具体是留多少呢
不难发现我们每次判断能不能删成零的条件是\(a_{i-1}|a_i\),因此为了让后面的\(a_{i+1}\)更容易整除\(a_i\),显然让\(a_i\)取最小值\(a_{i-1}\)是最优的
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=105;
int t,n,a[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; bool flag=1; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]);
for (i=2;i<=n;++i) if (a[i]%a[i-1]) flag=0; else a[i]=a[i-1];
puts(flag?"YES":"NO");
}
return 0;
}
B. Difference of GCDs
先说结论:对于每一个\(i\),找出它在\([l,r]\)中的任意一个倍数即可
证明:用类似归纳法一步步推,首先当\(i=1\)时我们把\(1\)作为\(\gcd\)用掉了
那么当\(i=2\)时,由于\(2\)和其它数的\(\gcd\le 2\),而且\(1\)被用掉了,因此我们只能取把\(2\)作为\(\gcd\)用掉,即找到\(2\)的倍数
同理,当\(i=3\)时,由于\(3\)和其它数的\(\gcd\le 3\),而且\(1,2\)被用掉了,因此我们只能取把\(3\)作为\(\gcd\)用掉,即找到\(3\)的倍数
以此类推,故得证
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int t,n,l,r,a[N];
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; bool flag=1; for (scanf("%d%d%d",&n,&l,&r),i=1;i<=n;++i)
if ((a[i]=r/i*i)<l) { flag=0; break; }
if (!flag) { puts("NO"); continue; }
for (puts("YES"),i=1;i<=n;++i) printf("%d%c",a[i]," \n"[i==n]);
}
return 0;
}
C. Doremy's IQ
刚开始弱智了,竟然WA了一发
首先一眼二分答案\(x\),然后naive地认为直接把前\(x\)小的比赛都打了,检验合法性即可
后来发现这个东西很假,因为当\(a_i\le q\)时可以无偿打比赛,因此顺序很重要
随后发现对于那些\(a_i<q\)的比赛,如果选择硬打那么肯定时在后面硬打来的划算
因此我们根据\(q-x\)来决定可以跳过前多少场\(a_i<q\)的比赛,然后再验证即可
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
struct data
{
int x,pos;
inline data(CI X=0,CI Pos=0) { x=X; pos=Pos; }
friend inline bool operator < (const data& A,const data& B)
{
return A.x==B.x?A.pos>B.pos:A.x<B.x;
}
}t[N]; int T,n,q,a[N],s[N];
inline bool check(CI x,int p=q)
{
int cur=n-x,num=0; for (RI i=1;i<=n;++i)
{
if (!p) { s[i]=0; continue; }
if (a[i]<=p) s[i]=1,++num; else
{
if (cur) s[i]=0,--cur; else s[i]=1,--p,++num;
}
}
return num>=x;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&T);T;--T)
{
RI i; for (scanf("%d%d",&n,&q),i=1;i<=n;++i)
scanf("%d",&a[i]),t[i]=data(a[i],i);
int l=1,r=n,ret; sort(t+1,t+n+1); while (l<=r)
{
int mid=l+r>>1; if (check(mid)) ret=mid,l=mid+1; else r=mid-1;
}
for (check(ret),i=1;i<=n;++i) putchar(s[i]?'1':'0'); putchar('\n');
}
return 0;
}
PS:好像还有一种不需要二分的做法:
考虑到前面的选择会影响后面,而后面的选择对前面无影响,因此我们考虑逆转问题
从后往前做,设初始时\(p=0\),每次如果\(a_i>p\)就给\(p\)加一
直到\(p=q\)后,这一段连续的后缀都可以选,然后对于前面的部分只有\(a_i\le q\)的选择打
代码略
D. Difference Array
刚开始真是毫无头绪的说,直到发现题目中的\(\sum_{i=1}^n a_i\le 5\times 10^5\)
直觉告诉我们此时一定会出现大量的\(0\),而不难发现我们可以把\(x\)个\(0\)看作\(1\)个\(0\),它对其它非\(0\)数的影响是相同的
然后直接每次暴力维护写一发,交上去发现过了的说
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
int t,n,a[N],ct; priority_queue < int,vector<int>,greater<int> > A,B;
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d",&n),i=1;i<=n;++i) scanf("%d",&a[i]);
for (i=2;i<=n;++i) A.push(a[i]-a[i-1]);
for (ct=0;!A.empty();A=B)
{
while (!A.empty()&&A.top()==0) A.pop(),++ct;
if (A.empty()) { puts("0"); break; }
if (A.size()==1) { printf("%d\n",A.top()); A.pop(); break; }
int pre=A.top(),now; A.pop();
while (!B.empty()) B.pop(); if (ct) --ct,B.push(pre);
while (!A.empty()) now=A.top(),A.pop(),B.push(now-pre),pre=now;
}
}
return 0;
}
关于这个算法的复杂度证明如下(以下默认\(a_i>0\)且\(a_1\le a_2\le \cdots \le a_n\)):
我们假设\(S=\sum_{i=1}^n a_i\),不难发现此时\(n-1+a_n\le S\),即\(n-1\le S-a_n\)
而在进行一次操作后\(S'=a_n-a_1\),而\(S-S'\ge n-1\),因此\(S\)至少减少\(n-1\)
因此我们每次花\(O(n\log n)\)的时间操作,数据量每次减少\(O(n)\)的规模,因此复杂度是有保证的
E. DFS Trees
首先考虑把正确的MST求出来,随便令某个点\(x\)为根
我们把剩下的非树边分为两类:
-
返祖边:联通某个点和它的祖先的边
-
横叉边:联通两个不同子树的边
考虑DFS的性质,显然若当以\(x\)为根时存在横叉边\((u,v)\)那么\(x\)就是不合法的,因为此时DFS到\(u/v\)的时候一定会先选\((u,v)\)导致原来的某条树边没选
我们不可能每次重新枚举根来做,因此考虑定下根,然后考虑每一条非树边\((u,v)\),此时细分两种情况(默认\(v\)的深度大于\(u\)):
-
\(u\)是\(v\)的祖先:
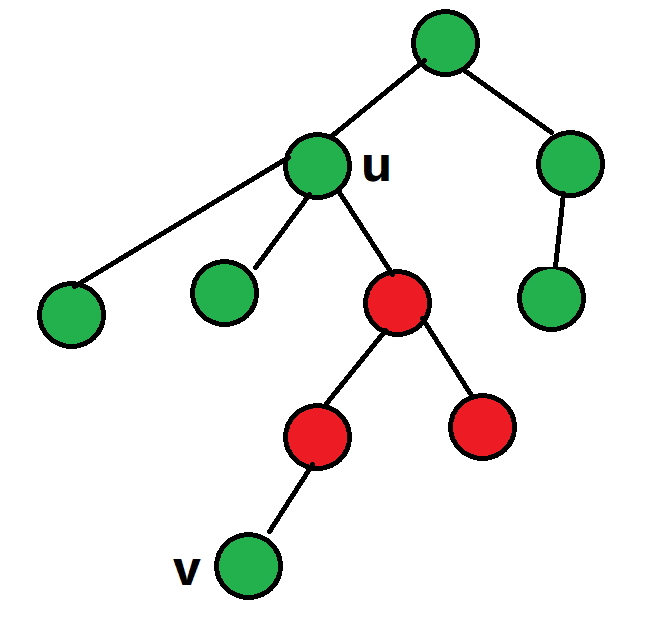
-
\(v\)不在\(u\)的子树内:
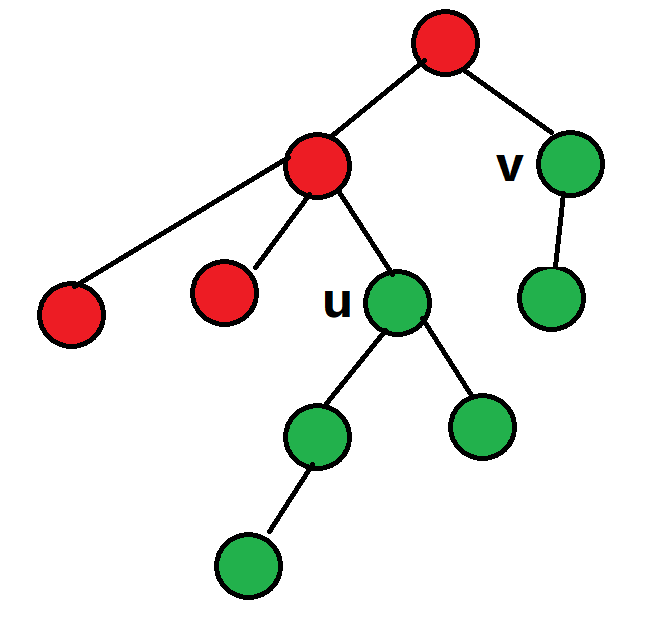
(设绿点表示此时可选择作为根的点,红点表示此时不可选择作为根的点)
不难发现如果我们用树上差分来维护\(f_i\),最后\(f_i=0\)的点为合法的,那么:
- 若\(u\)是\(v\)的祖先,设\(w\)为\(u\)的儿子且为\(v\)的祖先,则\(f_w\)加\(1\),\(f_v\)减\(1\)
- 若\(v\)不在\(u\)的子树内,则\(f_{root}\)加\(1\),\(f_u\)减\(1\),\(f_v\)减\(1\)
因此可以直接统计了,复杂度\(O(n\log n)\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005;
struct edge
{
int x,y;
inline edge(CI X=0,CI Y=0) { x=X; y=Y; }
}e[N<<1]; int t,n,m,x,y,tot,dep[N],dfn[N],sz[N],f[N];
namespace DSU
{
int fa[N];
inline void clear(void)
{
for (RI i=1;i<=n;++i) fa[i]=i;
}
inline int getfa(CI x)
{
return fa[x]==x?x:fa[x]=getfa(fa[x]);
}
inline bool query(CI x,CI y)
{
return getfa(x)==getfa(y);
}
inline void link(CI x,CI y)
{
fa[getfa(x)]=getfa(y);
}
};
namespace T
{
struct edge
{
int to,nxt;
}e[N<<1]; int tot,head[N],cnt,anc[N][20];
inline void addedge(CI x,CI y)
{
e[++cnt]=(edge){y,head[x]}; head[x]=cnt;
e[++cnt]=(edge){x,head[y]}; head[y]=cnt;
}
#define to e[i].to
inline void DFS1(CI now=1,CI fa=0)
{
dfn[now]=++tot; dep[now]=dep[anc[now][0]=fa]+1; sz[now]=1;
RI i; for (i=0;i<19;++i) if (anc[now][i]) anc[now][i+1]=anc[anc[now][i]][i]; else break;
for (i=head[now];i;i=e[i].nxt) if (to!=fa) DFS1(to,now),sz[now]+=sz[to];
}
inline void DFS2(CI now=1,CI fa=0)
{
for (RI i=head[now];i;i=e[i].nxt) if (to!=fa) f[to]+=f[now],DFS2(to,now);
}
inline int jump(int x,CI y)
{
for (RI i=19;~i;--i) if (dep[anc[x][i]]>dep[y]) x=anc[x][i]; return x;
}
#undef to
};
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%d%d",&n,&m),DSU::clear(),i=1;i<=m;++i)
if (scanf("%d%d",&x,&y),DSU::query(x,y)) e[++tot]=edge(x,y);
else T::addedge(x,y),DSU::link(x,y);
for (T::DFS1(),i=1;i<=tot;++i)
{
x=e[i].x; y=e[i].y; if (dep[x]<dep[y]) swap(x,y);
if (dfn[x]<dfn[y]||dfn[x]>dfn[y]+sz[y]-1) ++f[1],--f[x],--f[y];
else --f[x],++f[T::jump(x,y)];
}
for (T::DFS2(),i=1;i<=n;++i) putchar(f[i]?'0':'1'); putchar('\n');
return 0;
}
F. Partial Virtual Trees
好难的DP的说,完全做不来……
首先我们发现有一个限制\(S_1\ne S_2\)很恶心,因为这样我们不得不记录上一次选择的状态,直接爆炸
考虑用二项式反演搞掉这个限制,设\(F_i\)表示在\(i\)次操作后\(U=\{1\}\),但不强制要求\(S_1\ne S_2\)的方案数,\(G_i\)表示答案
考虑枚举\(F_i\)中有多少次操作满足\(S_1\ne S_2\),得到转移:
直接上二项式反演的形式二,得到:
因此现在目标变成了求\(F_i\),开始考虑树形DP
状态的设计是本题的难点,如果simple地设\(f_{u,k}\)表示子树\(u\)在经过\(k\)次操作后变为\(\{u\}\)的方案数,那么转移的时候由于要枚举子树内的所有点,复杂度会来到\(O(n^3)\)
于是我们巧妙地设计\(f_{u,k}\)表示子树\(u\)在经过\(k\)次操作后还有关键点的方案数,转移分为两类:
-
\(u\)在时刻\(k\)时仍然为关键点,此时要求每个子树内部都合法即可,则:
\[f_{u,k} \gets \prod_{v \in son_u} \sum_{i = 0}^k f_{v,i} \] -
\(u\)在时刻\(k\)时已经为非关键点,此时枚举它变为非关键点的时刻\(p\),那么在\([p+1,k]\)时刻\(u\)有且仅有一个儿子\(v\)的子树中有关键点,则:
考虑如何优化转移,不难发现我们需要记录下\(f_i\)的前缀和\(s_i\),对于那个少去某个数的累乘我们可以记录前/后缀积来处理,然后在进行前缀和处理即可
总复杂度\(O(n^2)\)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#define RI register int
#define CI const int&
using namespace std;
const int N=2005;
vector <int> v[N],son[N]; int n,mod,x,y,C[N][N],f[N][N],F[N],G[N],s[N][N],g[N][N],pre[N],suf[N];
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
inline void dec(int& x,CI y)
{
if ((x-=y)<0) x+=mod;
}
inline int sum(CI x,CI y)
{
return x+y>=mod?x+y-mod:x+y;
}
inline void DFS(CI now=1,CI fa=0)
{
RI i,j; f[now][0]=s[now][0]=1;
for (int to:v[now]) if (to!=fa) DFS(to,now),son[now].push_back(to);
for (j=0;j<n;++j)
{
int len=son[now].size(); pre[0]=suf[len+1]=1;
for (i=1;i<=len;++i) pre[i]=1LL*pre[i-1]*s[son[now][i-1]][j]%mod;
for (i=len;i;--i) suf[i]=1LL*suf[i+1]*s[son[now][i-1]][j]%mod;
for (i=1;i<=len;++i) g[son[now][i-1]][j]=1LL*pre[i-1]*suf[i+1]%mod;
}
for (int to:son[now]) for (i=1;i<=n;++i) inc(g[to][i],g[to][i-1]);
for (i=1;i<n;++i)
{
f[now][i]=1; for (int to:son[now]) f[now][i]=1LL*f[now][i]*s[to][i]%mod;
for (int to:son[now]) inc(f[now][i],1LL*f[to][i]*g[to][i-1]%mod);
}
for (i=1;i<n;++i) s[now][i]=sum(s[now][i-1],f[now][i]);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j; for (scanf("%d%d",&n,&mod),i=1;i<n;++i)
scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
for (C[0][0]=i=1;i<=n;++i) for (C[i][0]=j=1;j<=i;++j)
C[i][j]=sum(C[i-1][j-1],C[i-1][j]);
for (DFS(),i=1;i<n;++i)
{
F[i]=1; for (int to:son[1]) F[i]=1LL*F[i]*s[to][i-1]%mod;
}
for (i=1;i<n;++i) for (j=1;j<=i;++j)
{
int coef=1LL*F[j]*C[i][j]%mod;
if ((i-j)&1) dec(G[i],coef); else inc(G[i],coef);
}
for (i=1;i<n;++i) printf("%d%c",G[i]," \n"[i==n-1]);
return 0;
}
(Div. 1)E. Replace
稍微看了下感觉很可做啊,想了一个性质但没发现可以扩展,遗憾错过正解
对于区间查询问题,除了一些数据结构外,还有ST表这种划分区间的做法,因此我们考虑能不能合并两个区间的信息
首先我们发现,若\([l_1,r_1] \cup [l_2,r_2] = [l,r],[l_1,r_1] \cap [l_2,r_2] \neq \varnothing\),那么\(f(l,r) = f(l_1,r_1) \cup f(l_2,r_2),f(l_1,r_1) \cap f(l_2,r_2) \neq \varnothing\)
证明:令\([L,R]=[l_1,r_1]\bigcap [l_2,r_2]\),对于\(\forall i\in [L,R]\),\(\min\limits_{l_1\le k\le r_1} a_k\le a_i\le\max\limits_{l_1\le k\le r_1} a_k\)和\(\min\limits_{l_2\le k\le r_2} a_k\le a_i\le\max\limits_{l_2\le k\le r_2} a_k\)恒成立
因此
且
接下来再套用归纳法,不妨设\(f^k(l,r)\)为\([l,r]\)操作\(k\)次后的结果,则当满足上述限制
\([l_1,r_1] \cup [l_2,r_2] = [l,r],[l_1,r_1] \cap [l_2,r_2] \neq \varnothing\)时,\(f^k(l,r) = f^k(l_1,r_1) \cup f^k(l_2,r_2)\)
因此我们可以在ST表外面套一个倍增处理该问题,设\(L_{i,j,k}\)表示以\(i\)为左端点,长为\(2^j\)的区间,操作\(2^k\)次后得到的区间的左端点,\(R_{i,j,k}\)表示以\(i\)为左端点,长为\(2^j\)的区间,操作\(2^k\)次后得到的区间的右端点
预处理复杂度\(O(n\log^2 n)\),询问\(O(q\log n)\)
PS:直接像上面一样开数组会TLE,因为在开多维数组时一定要注意cache miss的问题,按照枚举的顺序从外往内从前往后调用比较快(快的不是一点半点)
#include<cstdio>
#include<iostream>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=100005,P=18;
int n,q,x,l,r,L[P][P][N],R[P][P][N],log[N];
inline int QL(CI k,CI l,CI r)
{
int t=log[r-l+1]; return min(L[k][t][l],L[k][t][r-(1<<t)+1]);
}
inline int QR(CI k,CI l,CI r)
{
int t=log[r-l+1]; return max(R[k][t][l],R[k][t][r-(1<<t)+1]);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j,k; for (scanf("%d%d",&n,&q),i=1;i<=n;++i)
scanf("%d",&x),L[0][0][i]=R[0][0][i]=x;
for (i=2;i<=n;++i) log[i]=log[i>>1]+1;
for (j=1;j<P;++j) for (i=1;i+(1<<j)-1<=n;++i)
L[0][j][i]=min(L[0][j-1][i],L[0][j-1][i+(1<<j-1)]),
R[0][j][i]=max(R[0][j-1][i],R[0][j-1][i+(1<<j-1)]);
for (k=1;k<P;++k) for (j=0;j<P;++j) for (i=1;i+(1<<j)-1<=n;++i)
L[k][j][i]=QL(k-1,L[k-1][j][i],R[k-1][j][i]),
R[k][j][i]=QR(k-1,L[k-1][j][i],R[k-1][j][i]);
while (q--)
{
scanf("%d%d",&l,&r); if (l==1&&r==n) { puts("0"); continue; }
int ans=0,nl,nr; for (i=P-1;~i;--i)
{
nl=QL(i,l,r); nr=QR(i,l,r);
if (nl!=1||nr!=n) l=nl,r=nr,ans+=(1<<i);
}
nl=QL(0,l,r); nr=QR(0,l,r); ++ans;
if (nl!=1||nr!=n) ans=-1; printf("%d\n",ans);
}
return 0;
}
Postscript
Div1的F有点仙扔了
复健过程中还没有遇到大码量的数据结构题的说,瑟瑟发抖