一、人工神经网络

人工智能的主流研究方法是连接主义,通过人工构建神经网络的方式模拟人类智能。
人工神经网络(Artificial Neural Network,即ANN ),是20世纪80 年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象, 建立某种简单模型,按不同的连接方式组成不同的网络。
人工神经网络借鉴了生物神经网络的思想,是超级简化版的生物神经网络。以工程技术手段模拟人脑神经系统的结构和功能,通过大量的非线性并行处理器模拟人脑中众多的神经元,用处理器复杂的连接关系模拟人脑中众多神经元之间的突触行为。
二、生物神经网络
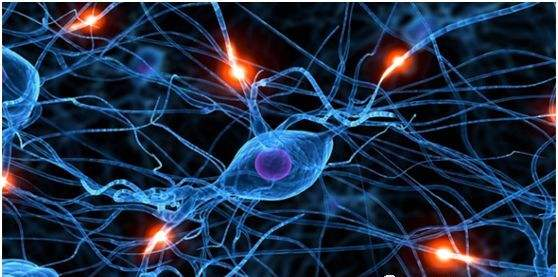
人脑由大约千亿个神经细胞及亿亿个神经突触组成,这些神经细胞及其突触共同构成了庞大的生物神经网络
- 每个神经元伸出的突起分为树突和轴突。
- 树突分支比较多,每个分支还可以再分支,长度一般比较短,作用是接受信号。
- 轴突只有一个,长度一般比较长,作用是把从树突和细胞表面传入细胞体的神经信号传出到其他神经元。
- 大脑中的神经元接受神经树突的兴奋性突触后电位和抑制性突触后电位,产生出沿其轴突传递的神经元的动作电位。

生物神经网络大概有以下特点:
- 每个神经元都是一个多输入单输出的信息处理单元,神经元输入分兴奋性输入和抑制性输入两种类型
- 神经细胞通过突触与其他神经细胞进行连接与通信,突触所接收到的信号强度超过某个阈值时,神经细胞会进入激活状态,并通过突触向上层神经细胞发送激活细号
- 神经元具有空间整合特性和阈值特性, 较高层次的神经元加工出了较低层次不具备的“新功能”
- 神经元输入与输出间有固定的时滞,主要取决于突触延搁
外部事物属性一般以光波、声波、电波等方式作为输入,刺激人类的生物传感器。
三、硅基智能与碳基智能
人类智能建立在有机物基础上的碳基智能,而人工智能建立在无机物基础上的硅基智能。
碳基智能与硅基智能的本质区别是架构,决定了数据的传输与处理是否能够同时进行。
计算机:硅基智能

数据的传输与处理无法同步进行。
冯·诺伊曼结构体系的一个核心特征是运算单元和存储单元的分离,两者由数据总线连接。
运算单元需要从数据总线接收来自存储单元的数据,运算完成后再将运算结果通过数据总线传回给存储单元
数据不是为了存储而存储,而是为了在需要时能够快速提取而存储,存储的作用是提升数据处理的有效性
人脑:碳基智能
数据的传输和处理是同步进行的。
数据的传输和处理由突触和神经元之间的交互完成,并且是同时进行的,不存在先传输后处理的顺序。
在同样的时间和空间上,哺乳动物的大脑能在分布式的神经系统上交换和处理信息,这是计算机达不到的。
生物记忆是一个保留精华的过程,无法用简单的存储模拟生物记忆。
四、MP模型

M-P模型,是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。
MP神经元接受一个或多个输入,并对输入的线性加权进行非线性处理以产生输出。
假定MP神经元输入信号是N+1维向量((x_0,x_1,...,x_N)),第i个分量的权重为(w_i),则输出可以写成
(y=ϕ(sum_{i=0}^Nw_ix_i))
(ϕ(⋅))是传递函数,用于将加权后的输入转换为输出,通常被设计成连续且有界的非线性增函数。
在MP神经元中,麦卡洛克和皮茨将输入和输出都限定为二进制信号,使用的传递函数则是不连续的符号函数,符号函数以预先设定的阈值作为参数:当输入大于阈值时,符号函数输出 1,反之则输出 0
这样MP神经元工作就类似数字电路中的逻辑门,能够实现“逻辑与”或者“逻辑或”的功能.
感知器——最简单的神经网络结构

在1958年,美国心理学家Frank Rosenblatt提出一种具有单层计算单元的神经网络,称为感知器(Perceptron)。它其实就是基于M-P模型的结构。
Frank受到1949 年加拿大心理学家唐纳德·赫布提出的“赫布理论”,核心观点是学习的过程主要是通过神经元之间突触的形成和变化来实现的。
两个神经元细胞之间进行交流的越多,它们之间的联系就越来越强化,学习的效果也在联系不断强化的过程中逐渐产生。
从人工神经网络的角度,这个理论的意义在于给出了改变模型神经元之间权重的准则
- 如果两个神经元同时被激活,它们的权重应该增加
- 如果两个神经元分别被激活,两者的权重应该降低

感知器不是真实的器件,而是一种二分类的监督学习算法,能够决定向量表示的输入是不属于某个特定类别。
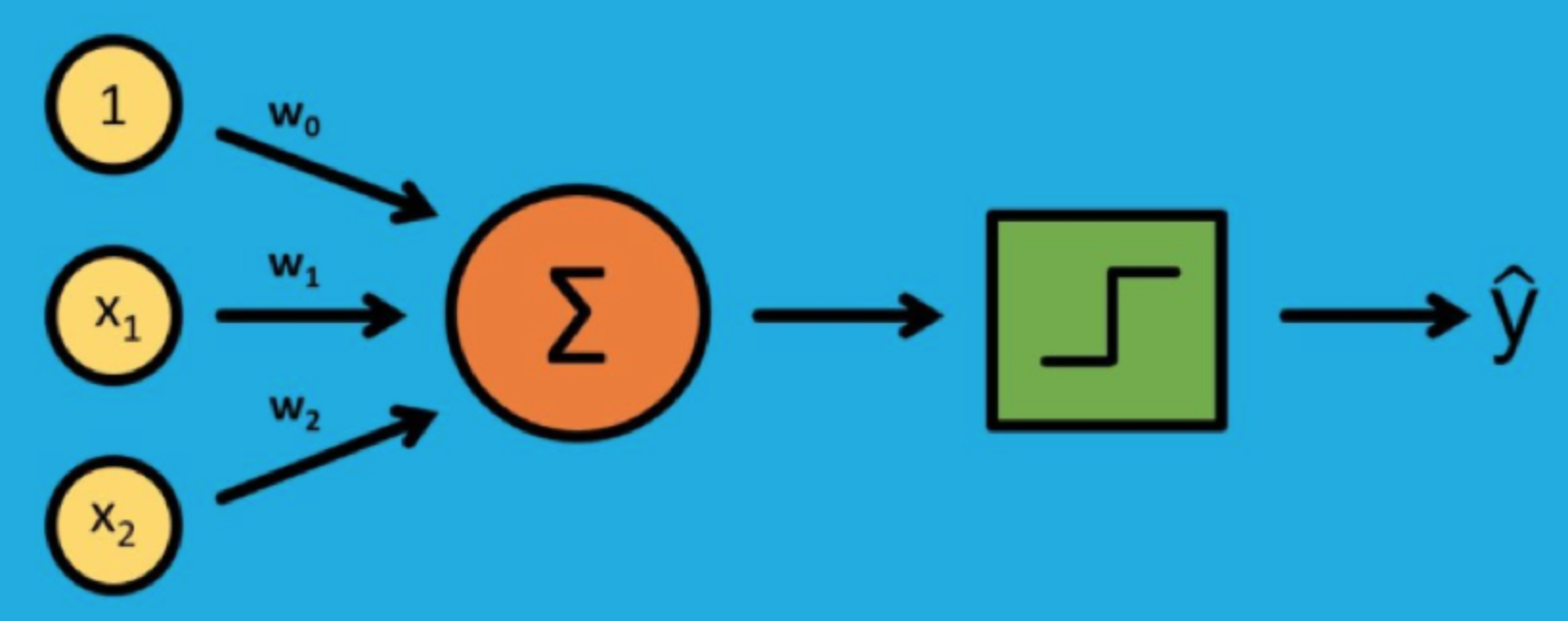
感知器由输入导和输出导组成,输入导负责接收外界信号,输出导是MP神经元,也就是阈值逻辑单元。
每个输入信号(特征)都以一定的权重送入MP神经元中,MP神经元则利用符号将特征的线性组合映射为分类输出。
给一个包含若干输入输出对应关系实例的训练集,学习步骤为:
- 初始化权重w(0)和阈值,其中权重可以初始化为0或较小的随机娄
- 对训练集中的第j个样本,将其输入向量(x_j)送入已经初始化的感知器,得到输出(y_j(t))
- 根据(y_j(t))和样本(j)的给定输出结果(d_j),按以规则更新权重向量:
(w_i(t+1)=w_i(t)+η[d_j-y_j(t)]⋅x_{j,i}) - 重复以上两个步骤,直到训练次数达到预设值
第三步要对感知器的权重进行更新,是学习算法的核心步骤,其中0<η≤1 被称为学习率参数,是修正误差的一个比例系数。
如果分类结果和真实结果相同,则保持权重不变;如果输出值应该为0但实际为1,就要减少(x_j)中输入值为1的分量的权重;如果输出值应该为1但实际为0,则增加(x_j)中输入值为1的分量的权重
感知器能够学习的前提是它具有收敛性。感知器学习算法能够在有限次的迭代后收敛,得到决策面位于两类之间的超平面。
本质上在执行二分类问题时,感知器以所有误差分类点到超平面的总距离为损失函数,用随机梯度下降法不断使损失函数下降,直到得到正确的分类结果
除了优良的收敛性能外,感知器还有自适应性,只要给定训练数据集,算法就可以基于误差修正自适应地调整参数而无需人工介入,这在MP神经元的有了很大的进步。
单层感知器——无法处理异或问题
只能解决线性分类问题,没有办法处理异或问题
所谓线性分类意指所有的正例和负例可以通过高维空间中的一个超平面完全分开而不产生错误。
如果一个圆形被分成一黑一白两个半圆,这就是个线性可分的问题;
可如果是个太极图的话,单单一条直线就没法把黑色和白色完全区分开来了,这对应着线性不可分问题。
如果训练数据集不是线性可分的,也就是正例不能通过超平面与负例分离,那么感知器就不可能将所有输入向量正确分类。
多层感知器——隐藏层、反向传播

多层感知器解决了异或问题,在输入与输出层之间添加了隐藏层,采用了反向传播的方式。
-
隐藏层
多层感知器的核心结构是隐藏层,用于特征检测。
之所以被称为隐藏层,是因为这些神经元并不属于网络的输入或输出。
隐藏的神经元将训练数据变换到新的特征空间上,并识别出训练数据的突出特征。
不同层之间,多导感知器具有全连接性,即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接,连接的强度由网络中的权重系统决定。 -
反向传播
将输出和真实值相减得到误差函数,最后根据误差函数更新权重。
训练过程中,虽然信号的流向是输出方向,但是计算的误差函数和信号传播的方向相反,这种学习方式叫反向传播。
通过求解误差函数关于每个权重系数的偏导数,以此使误差最小化来训练整个网络。