今天dp发现一道背包方案数的题,先是看错题目(丢人),然后是循环不会搞(丢人)。
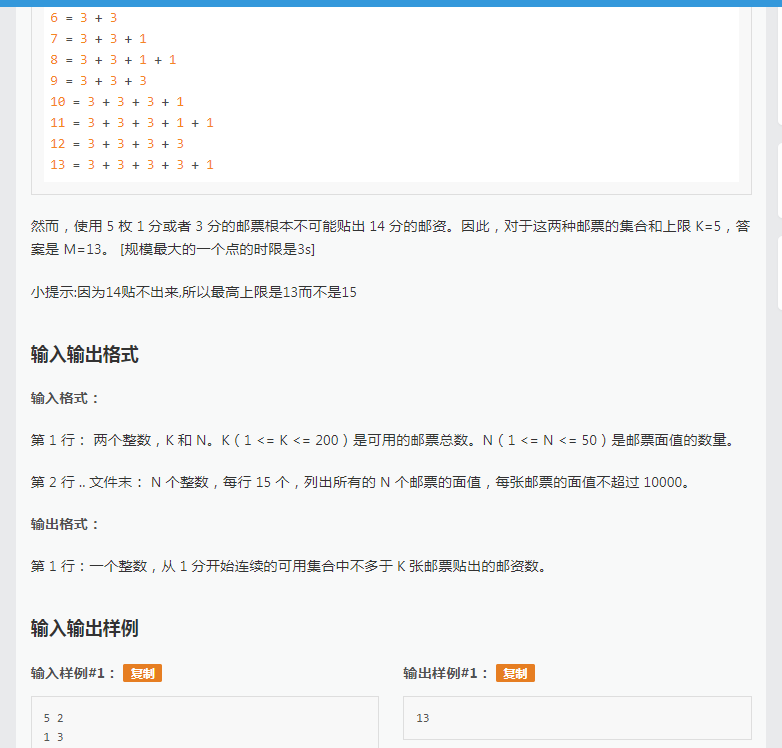
首先是本人看错题想出来的变式:求能拼成的方案总数这个的话既不是完全背包也不是普通的01背包,所以考虑按照01背包的方案数来求解。
设f[i]表示当前的价值能否拼出,f[0]=1;f[i] | =f[i-a[j]];这个地方或一下(这个操作第一次使用重视一下)意思感性理解一下很简单。
然后是循环的问题三重循环的位置打反了,关键是没有考虑好更新时候的状态安排,要不然是不可能打反的,这里注意第一层循环是物品的数量,第二重循环就要倒着枚举背包的价值了,因为在当前的数量面前它的数量并非无限所以需要01背包的倒着循环而多次的话通过第一层循环来增加。
第三重循环则是枚举物品的价值了,状态转移的时候k记得要判断>=a[j]不然re。。。
代码:

#include<iostream> #include<cmath> #include<cstdio> #include<cstring> #include<string> #include<ctime> #include<vector> #include<map> #include<queue> #include<iomanip> #include<stack> #include<algorithm> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*f; } int n,m; int a[100],ans=0; int f[1002],maxx=-1; int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { a[i]=read(); maxx=max(maxx,a[i]); } f[0]=1;maxx*=n; for(int i=1;i<=n;i++) for(int k=maxx;k>=0;k--) for(int j=1;j<=m;j++)if(k>=f[j])f[k]|=f[k-a[j]]; for(int i=1;i<=maxx;i++) if(f[i]!=0)ans++; printf("%d ",ans); return 0; }
看错题了真是尴尬,那么这道原题对于我这个dp蒟蒻,还是好难啊。
这道题的正解是一个01完全背包限制一下数量再进行转移即可。。。

#include<iostream> #include<cmath> #include<cstdio> #include<cstring> #include<string> #include<ctime> #include<vector> #include<map> #include<queue> #include<iomanip> #include<stack> #include<algorithm> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return x*f; } const int wy=1999999; int n,m; int ans=0,maxx=-1; int a[100],f[2000010];//f[i]表示第i个价值被最少的物品拼成 int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { a[i]=read(); maxx=max(maxx,a[i]); } maxx*=n; for(int i=1;i<=maxx;i++)f[i]=wy; f[0]=0; for(int i=1;i<=m;i++) for(int j=a[i];j<=maxx;j++) { if(f[j-a[i]]+1<=n)f[j]=min(f[j],f[j-a[i]]+1); } for(int i=1;i<=maxx;i++) { if(f[i]==wy){printf("%d ",i-1);return 0;} } printf("%d ",maxx); return 0; }
磐石不转守四方——《全职高手》
