区间dp后就开垦树形dp了,树形dp其实就是把dp的过程在一棵树上进行,表现形式也很简单呢,其实就是子节点和父亲节点的关系之间的dp过程往往都是从一个没有儿子的儿子节点开始dp这样才能形成最优子结构,思考一下状态转移,当然是直接看书上的状态转移了(感觉很自然的状态转移。
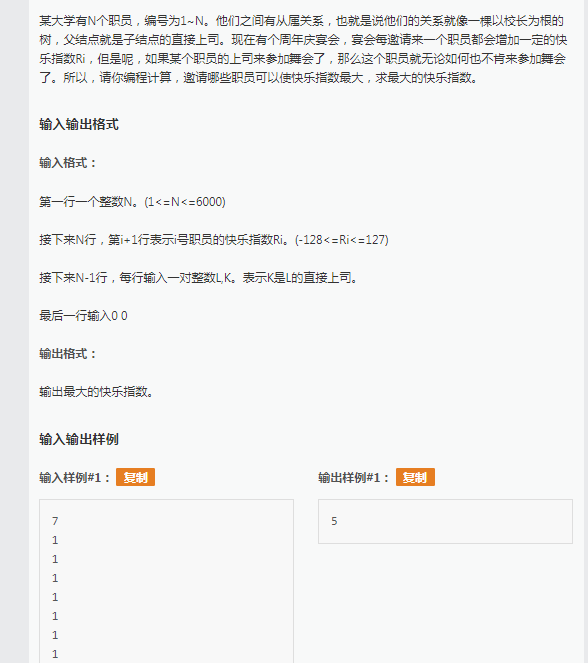
这里父亲和儿子的关系已经给的很明显了,设f[i][1/0]表示当前这个人出席还是不出席,然后从儿子转移到父亲,形成最优子结构。
转移方程:f[x][1]+=f[y][0];/f[x][0]+=max(f[y][1],f[y][0]);还得小小的初始化一下。关于无后效性的问题的话我想应该是f数组能把所有最优的状态保存下来然后进行调用所以最后不需要具有无后效性,最后答案就是max(f[root][0],f[root][1]);这样这一道树形dp入门题就被完美解决了。
代码:

#include<bits/stdc++.h> #include<iostream> #include<string> #include<cstring> #include<cstdio> #include<ctime> #include<iomanip> #include<vector> #include<queue> #include<map> #include<stack> #include<cmath> #include<algorithm> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=6002; int n,m,root; int v[maxn],ru[maxn],f[maxn][2];//f[i][0]表示当前这个上司不参加,f[i][1]表示当前这个上司参加。 int lin[maxn],ver[maxn],nex[maxn],len=0; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dp(int x) { f[x][1]=v[x]; f[x][0]=0; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i];dp(tn); f[x][1]+=f[tn][0]; f[x][0]+=max(f[tn][0],f[tn][1]); } } int main() { n=read(); for(int i=1;i<=n;i++)v[i]=read(); for(int i=1;i<=n;i++) { int x,y;x=read();y=read(); if(x!=0)add(y,x),ru[x]=1; } for(int i=1;i<=n;i++)if(ru[i]==0){root=i;break;} dp(root); printf("%d ",max(f[root][1],f[root][0])); return 0; }
树形dp的入门题,还有一个类似的。

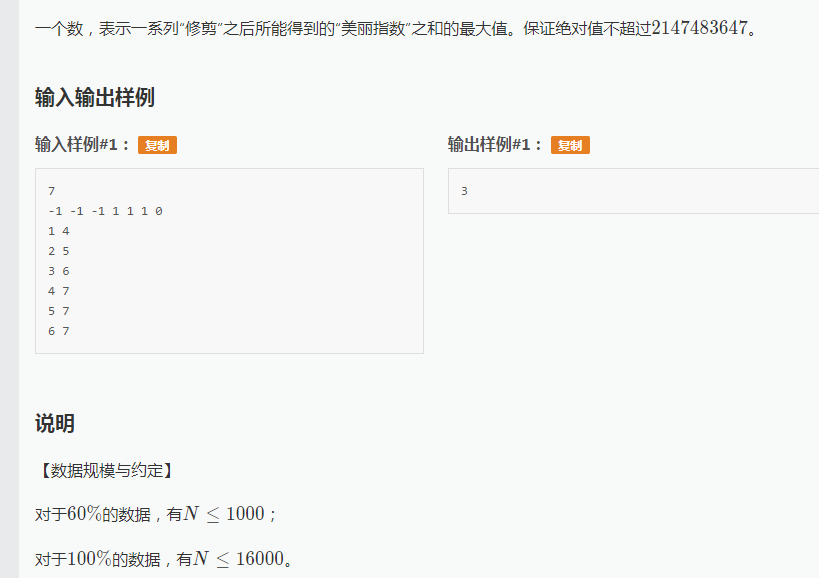
给出棵树要求子树和最大,这就很显然了,首先设f[i][0/1]表示当前节点i选还是不选。进行状态转移即可。

#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<iomanip> #include<cmath> #include<ctime> #include<vector> #include<stack> #include<queue> #include<map> #include<algorithm> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=16002; int n,m; int f[maxn][2],v[maxn],ans=0,vis[maxn]; int ver[maxn<<1],lin[maxn<<1],nex[maxn<<1],len=0; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dfs(int x) { vis[x]=1;f[x][0]=0;f[x][1]=v[x]; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; if(vis[tn]==0) { dfs(tn); f[x][1]+=max(f[tn][0],f[tn][1]); } } } int main() { //freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++)v[i]=read(); for(int i=1;i<n;i++) { int x,y; x=read();y=read(); add(x,y);add(y,x); } dfs(1); for(int i=1;i<=n;i++)ans=max(ans,f[i][1]); printf("%d ",ans); return 0; }
下面是一道比较难理解的背包类树形dp(背包搞得很熟的话其实很简单。

在n门课中选择m个科目,不过每个科目有父子之间的关系,选儿子必须选父亲,当然这也并不是一道纯正的分组背包了,因为在每一组中不一定只能选一个,而且这是一棵树形的背包,有些偏向有依赖性背包,如金明的预算方案,我想这道题可以用树形dp写。
首先还是进行考虑从儿子优先就是找到一个没有儿子的儿子,对这个点进行背包,然后强制取当前点的父亲,多余的细节看代码。
代码:

#include<bits/stdc++.h> #include<iostream> #include<string> #include<cstring> #include<cstdio> #include<ctime> #include<iomanip> #include<vector> #include<queue> #include<map> #include<stack> #include<cmath> #include<algorithm> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=302; int n,m; int v[maxn]; int lin[maxn],nex[maxn],ver[maxn],len=0,f[maxn][maxn]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dp(int x) { f[x][0]=0; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i];dp(tn); for(int j=m;j>=0;j--)//共取m个科目 for(int t=0;t<=j;t++)//对儿子的话取j个科目进行转移 if(j>=t)f[x][j]=max(f[x][j],f[x][j-t]+f[tn][t]); } if(x!=0)for(int j=m;j>=1;j--)f[x][j]=f[x][j-1]+v[x];//强制选择父亲 } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++){int x;x=read(),v[i]=read(),add(x,i);} dp(0); printf("%d ",f[0][m]); return 0; }
针对此代码,发现状态转移是只是针对每一门课程占用体积都为1进行的,下面是当体积都不为1的时候进行的转移,复杂度依然是nm^2.

#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<iomanip> #include<cmath> #include<ctime> #include<vector> #include<stack> #include<queue> #include<map> #include<algorithm> using namespace std; inline int read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int maxn=502; int n,m; int lin[maxn<<1],nex[maxn<<1],ver[maxn<<1],len=0; int f[maxn][maxn],v[maxn],w[maxn]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dfs(int x) { for(int j=w[x];j<=m;j++)f[x][j]=v[x]; for(int i=lin[x];i;i=nex[i]) { int tn=ver[i];dfs(tn); for(int j=m-w[x];j>=0;j--) for(int k=1;k<=j;k++) f[x][j+w[x]]=max(f[x][j+w[x]],f[x][j+w[x]-k]+f[tn][k]); } } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { int x; x=read();v[i]=read(); add(x,i); } w[0]=0;for(int i=1;i<=n;i++)w[i]=1;//预处理出所有课程的体积 dfs(0); printf("%d ",f[0][m]); return 0; }
上述只不过是书上直接dp,类似于背包的做法,值得一提的是这种做法并不多见,一般深入题目就会看出这其实是一棵多叉树,运用左儿子右兄弟的做法即可把多叉树转化成二叉树。

#include<bits/stdc++.h> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<iomanip> #include<cmath> #include<ctime> #include<vector> #include<stack> #include<queue> #include<map> #include<algorithm> using namespace std; inline int read() { long long x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } // .-~~~~~~~~~-._ _.-~~~~~~~~~-. // __.' ~. .~ `.__ // .'// ./ \`. // .'// | \`. // .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \`. // .'//.-" `-. | .-' "-.\`. // .'//______.============-.. | / ..-============.______\`. // .'______________________________|/______________________________`. //选课 const int maxn=1000; int n,m; int ls[maxn],rx[maxn];//l是左,r是右,左儿子,右兄弟 int a[maxn],f[maxn][maxn]; void dfs(int i,int j) { if(f[i][j]>0||j==0||i==0)return;//类似于记忆化搜索,搜过的就不再搜 //printf("%d ",i); dfs(rx[i],j);//不选当前节点的话就去判断他的右兄弟 f[i][j]=max(f[i][j],f[rx[i]][j]);//和它的右兄弟之间的最优值进行比较 for(int k=0;k<=j-1;k++)//如果选择当前节点的话k取值就是[0,j-1]当前节点要选 { dfs(ls[i],j-k-1);//针对当前节点判断它的左儿子节点 dfs(rx[i],k);//再次跑一遍它的右兄弟和上次情况不同 f[i][j]=max(f[i][j],f[rx[i]][k]+f[ls[i]][j-k-1]+a[i]); //当前节点的最优解f由它的右兄弟和它的左儿子之间的价值之和 } } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { int x; x=read();a[i]=read(); if(x==0)x=n+1; rx[i]=ls[x]; ls[x]=i; } //for(int i=1;i<=n;i++)printf("%d ",a[i]); //cout<<rx[rx[ls[rx[ls[n+1]]]]]; //cout<<m<<endl; dfs(ls[n+1],m); printf("%d ",f[ls[n+1]][m]); return 0; }
当然还有更优秀的算法,复杂度nm。把当前要更新的父亲的信息全部传入让儿子节点进行dp。

#include<iostream> #include<cmath> #include<ctime> #include<cstdio> #include<iomanip> #include<cstring> #include<string> #include<stack> #include<algorithm> #include<map> #include<queue> #include<deque> #include<vector> #include<set> using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } void put(int x) { if(x==0){putchar('0');putchar(' ');return;} if(x<0){x=-x;putchar('-');} int num=0;char ch[50]; while(x)ch[++num]=x%10+'0',x/=10; while(num)putchar(ch[num--]); putchar(' ');return; } const int maxn=400; int n,m; int lin[maxn<<1],ver[maxn<<1],nex[maxn<<1],len=0; int v[maxn],w[maxn],f[maxn][maxn]; void add(int x,int y) { ver[++len]=y; nex[len]=lin[x]; lin[x]=len; } void dfs(int x) { for(int i=lin[x];i;i=nex[i]) { int tn=ver[i]; for(int j=1;j<=m;j++)f[tn][j]=f[x][j]; dfs(tn); for(int j=m;j>=w[tn];j--) f[x][j]=max(f[x][j],f[tn][j-w[tn]]+v[tn]); } } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { int x; x=read();v[i]=read(); add(x,i); } for(int i=1;i<=n;i++)w[i]=1;w[0]=0; dfs(0); printf("%d ",f[0][m]); return 0; }
懂我的人不必解释,不懂我的人,何必解释。
