参考这篇文章:
https://zhuanlan.zhihu.com/p/33173246
https://www.sohu.com/a/220228574_717210(这篇是上面的转载)
其中ICS问题参考这里:
https://blog.csdn.net/sinat_33741547/article/details/87158830
深度神经网络涉及到很多层的叠加,而每一层的参数更新会导致上层的输入数据分布发生变化,通过层层叠加,高层的输入分布变化会非常剧烈,这就使得高层需要不断去重新适应底层的参数更新。为了训好模型,我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。
Google 将这一现象总结为 Internal Covariate Shift,简称 ICS.
IID独立同分布假设

1.独立同分布independent and identically distributed (i.i.d.) 在概率统计理论中,如果变量序列或者其他随机变量有相同的概率分布,并且互相独立,那么这些随机变量是独立同分布。 在西瓜书中解释是:输入空间中的所有样本服从一个隐含未知的分布,训练数据所有样本都是独立地从这个分布上采样而得。 2.简单解释独立、同分布、独立同分布 (1)独立:每次抽样之间没有关系,不会相互影响 举例:给一个骰子,每次抛骰子抛到几就是几,这是独立;如果我要抛骰子两次之和大于8,那么第一次和第二次抛就不独立,因为第二次抛的结果和第一次相关。 (2)同分布:每次抽样,样本服从同一个分布 举例:给一个骰子,每次抛骰子得到任意点数的概率都是六分之一,这个就是同分布 (3)独立同分布:i,i,d,每次抽样之间独立而且同分布 3.机器学习领域的重要假设 IID独立同分布。即假设训练数据和测试数据是满足相同分布的,它是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。 4.目前 机器学习并不总要求独立同分布,在不少问题中要求样本数据采样自同一个分布是因为希望用训练数据集得到的模型可以合理的用于测试数据集,使用独立同分布假设能够解释得通。 目前一些机器学习内容已经不再囿于独立同分布假设下,一些问题会假设样本没有同分布。 ———————————————— 版权声明:本文为CSDN博主「Magic--Rain」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/weixin_41847115/article/details/82956256
可以看到,随着网络层数的加深,输入分布经过多次线性非线性变换,已经被改变了,但是它对应的标签,如分类,还是一致的,即使条件概率一致,边缘概率不同。
因此,每个神经元的输入数据不再是“独立同分布”,导致了以下问题:
1、上层网络需要不断适应新的输入数据分布,降低学习速度。 2、下层输入的变化可能趋向于变大或者变小,导致上层落入饱和区,使得学习过早停止。 3、每层的更新都会影响到其它层,因此每层的参数更新策略需要尽可能的谨慎。
解决思想

前面说到,出现上述问题的根本原因是神经网络每层之间,无法满足基本假设"独立同分布",那么思路应该是怎么使得输入分布满足独立同分布。 白化(Whitening) 白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。 白化是对输入数据分布进行变换,进而达到以下两个目的: 1、使得输入特征分布具有相同的均值与方差,其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同; 2、去除特征之间的相关性。 通过白化操作,我们可以减缓ICS的问题,进而固定了每一层网络输入分布,加速网络训练过程的收敛。 Normalization 但是白化计算成本太高,每一轮训练中的每一层都需要做白化操作;同时白化改变了网络每一层的分布,导致网络层中数据的表达能力受限。 因此提出了normalization方法,能够简化计算过程;又能够让数据尽可能保留原始的表达能力。 ———————————————— 版权声明:本文为CSDN博主「lpty」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。 原文链接:https://blog.csdn.net/sinat_33741547/article/details/87158830
回到这篇文章:
https://www.sohu.com/a/220228574_717210
机器学习界的炼丹师们最喜欢的数据有什么特点?窃以为,莫过于 “独立同分布” 了,即independent and identically distributed,简称为 i.i.d.
(比如 Naive Bayes 模型就建立在特征彼此独立的基础之上,而 Logistic Regression 和 神经网络 则在非独立的特征数据上依然可以训练出很好的模型)
因此,在把数据喂给机器学习模型之前,“白化(whitening)” 是一个重要的数据预处理步骤。白化一般包含两个目的:
(1)去除特征之间的相关性 —> 独立;
(2)使得所有特征具有相同的均值和方差 —> 同分布。
白化最典型的方法就是 PCA。
3. 主流 Normalization 方法梳理
在上一节中,我们提炼了 Normalization 的通用公式:
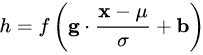
对照于这一公式,我们来梳理主流的四种规范化方法。
3.1 Batch Normalization —— 纵向规范化
以 BN 为代表的 Normalization 方法退而求其次,进行了简化的白化操作。基本思想是:在将 x 送给神经元之前,先对其做平移和伸缩变换, 将 x 的分布规范化成在固定区间范围的标准分布。
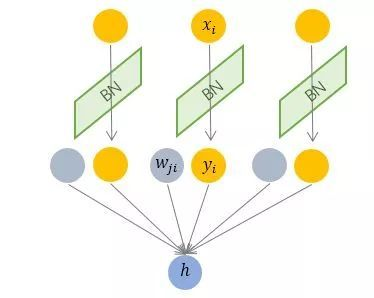
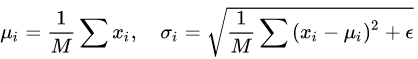
按上图所示,相对于一层神经元的水平排列,BN 可以看做一种纵向的规范化。由于 BN 是针对单个维度定义的,因此标准公式中的计算均为 element-wise 的。
3.2 Layer Normalization —— 横向规范化
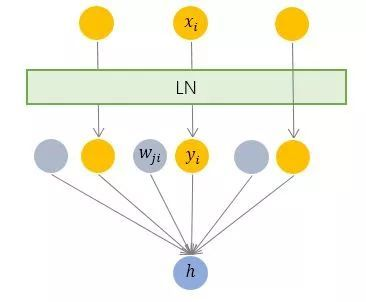
它综合考虑一层所有维度的输入,计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
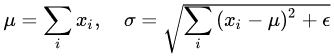
对应到标准公式中,四大参数 μ,σ,g,b 均为标量(BN 中是向量),所有输入共享一个规范化变换。
LN 针对单个训练样本进行,不依赖于其他数据,因此可以避免 BN 中受 mini-batch 数据分布影响的问题,可以用于 小 mini-batch 场景、动态网络场景和 RNN,特别是自然语言处理领域。此外,LN 不需要保存 mini-batch 的均值和方差,节省了额外的存储空间。
而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。
3.3 Weight Normalization —— 参数规范化
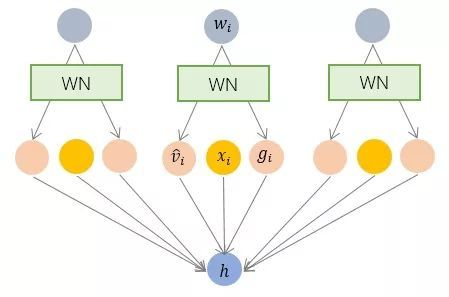
BN 和 LN 均将规范化应用于输入的特征数据 x,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 w,这就是 WN 名称的来源。
WN 提出的方案是,将权重向量 w 分解为向量方向v和向量模 g 两部分:其中 v 是与 w 同维度的向量,是欧氏范数,因此是单位向量,决定了 w 的方向;g 是标量,决定了 w 的长度。由于,因此这一权重分解的方式将权重向量的欧氏范数进行了固定,从而实现了正则化的效果。

3.4 Cosine Normalization —— 余弦规范化
对输入数据 x 的变换已经做过了,横着来是 LN,纵着来是 BN。
对模型参数 w 的变换也已经做过了,就是 WN。
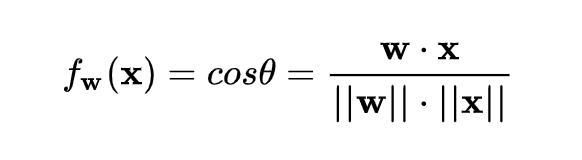
4. Normalization 为什么会有效?
4.1 Normalization 的权重伸缩不变性
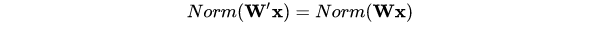
权重伸缩不变性可以有效地提高反向传播的效率
4.2 Normalization 的数据伸缩不变性
