本文为IMU预积分总结与公式推导系列技术报告的第二篇。
承接第一篇的内容,本篇将推导IMU预积分的测量值,并分析其测量误差的分布形式。
传统捷联惯性导航的递推算法,以初始状态为基础,利用IMU测量得到的比力和角速度信息进行积分运算,实时更新载体的位姿及速度等状态,回顾上一篇给出的运动模型,如果已知k时刻的载体状态Rk、vk和pk,则利用IMU测量值可以直接递推得到k+1时刻的载体状态,根据这种思路,如果知道上一帧图像采样时刻载体的位姿和速度,则可以递推得到当前帧的位姿和速度。需要注意的是,传统的惯导解算中非常重要的一个问题是处理重力,由于加计的测量特性,其测量值为包含反向重力的比力,而不是纯加速度。这使得一旦姿态不准确,重力投影误差将对速度和位置积分产生严重影响。
在基于BA的视觉惯性融合算法中,各个节点的载体状态都是有待优化的量。IMU预积分的初衷,是希望借鉴纯视觉SLAM中图优化的思想,将帧与帧之间IMU相对测量信息转换为约束节点(载体位姿)的边参与到优化框架中。IMU预积分理论最大的贡献是对这些IMU相对测量进行处理,使得它与绝对位姿解耦(或者只需要线性运算就可以进行校正),从而大大提高优化速度。另外,这种优化架构还使得加计测量中不受待见的重力变成一个有利条件——重力的存在将使整个系统对绝对姿态(指相对水平地理坐标系的俯仰角和横滚角,不包括真航向)可观。要知道纯视觉VO或者SLAM是完全无法得到绝对姿态的。
此外,由于传感器测量误差的存在,无论是纯惯导还是纯VO解算,单纯依靠递推运算不可避免的将带来累积误差(低精度IMU会极快发散)。将两种传感器融合可以利用冗余测量(例如两种方式都可以求取相对位姿)来抑制累积误差。同时,IMU和视觉这两种不同源的测量,也使得IMU的bias可观,从而可以在优化中被有效估计。另外老生常谈的纯单目视觉缺乏绝对尺度的问题,也可以由惯性信息的引入而得以解决。
罗里吧嗦了一大堆,下面我们就来看看IMU预积分中是如何处理相对测量的。







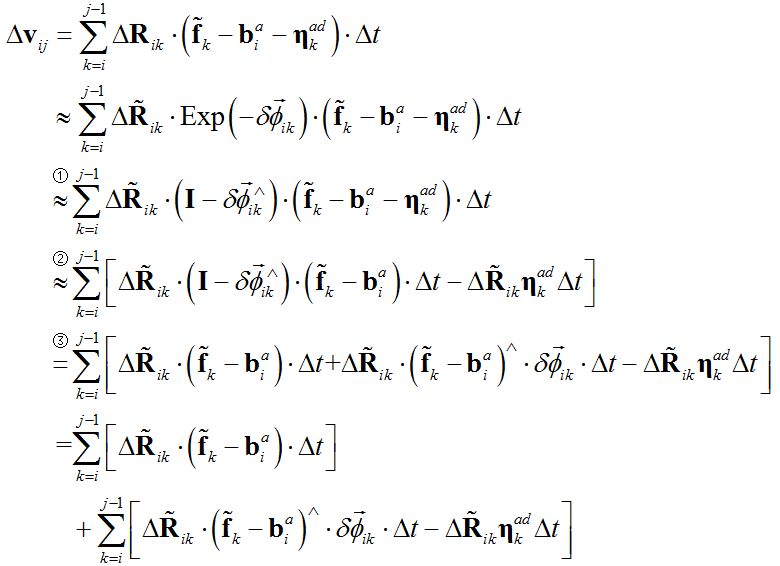


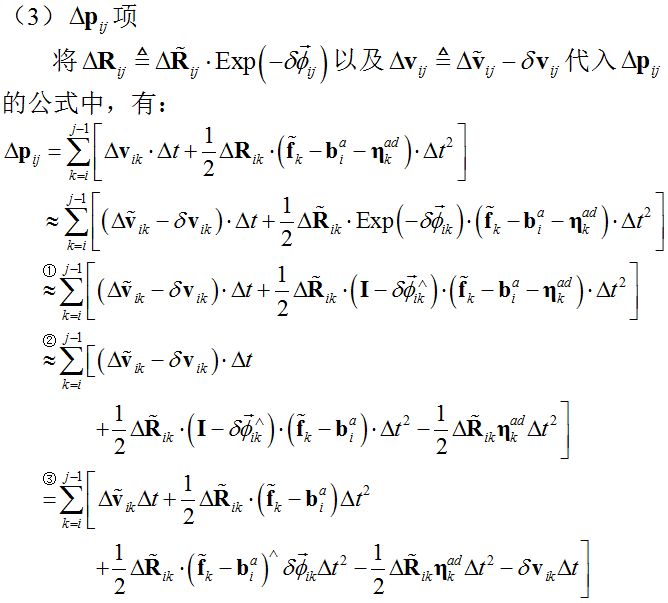




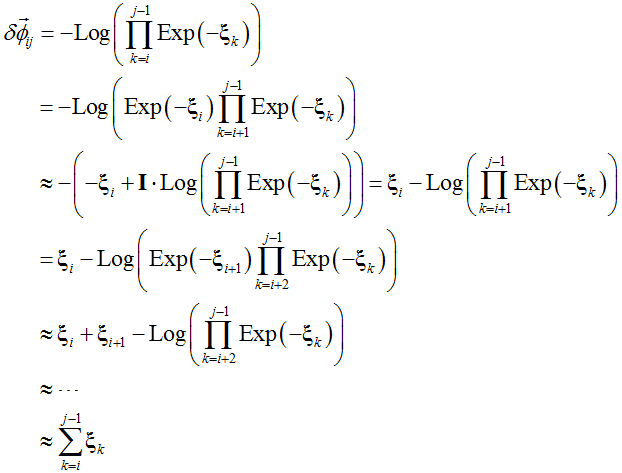




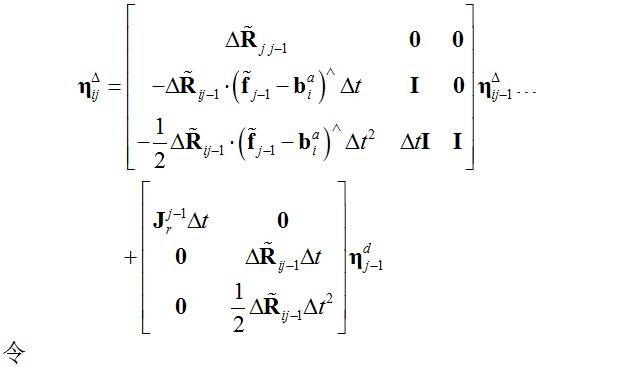

本篇对IMU预积分的理想模型及其噪声展开部分的公式进行了分析和推导。噪声分布将用来计算IMU预积分的信息矩阵,在优化框架中起到平衡权重的作用。