我们经常将归一化和标准化弄混淆,下面简单描述一下他们之间的差异
归一化(Normalization)
归一化的目标是找到某种映射关系,将原数据映射到[a,b]区间上。一般a,b会取[−1,1],[0,1]这些组合
一般有两种应用场景:
-
把数变为(0, 1)之间的小数
-
把有量纲的数转化为无量纲的数
常用min-max normalization:
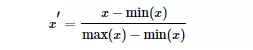
标准化(Standardization)
用大数定理将数据转化为一个标准正态分布,标准化公式为:
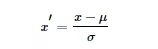
归一化和标准化的区别
我们可以这样简单地解释:归一化的缩放是“拍扁”统一到区间(仅由极值决定),而标准化的缩放是更加“弹性”和“动态”的,和整体样本的分布有很大的关系。
值得注意:归一化:缩放仅仅跟最大、最小值的差别有关。标准化:缩放和每个点都有关系,通过方差(variance)体现出来。与归一化对比,标准化中所有数据点都有贡献(通过均值和标准差造成影响)。
为什么要标准化和归一化?
-
提升模型精度:归一化后,不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)
-
加速模型收敛:标准化后,最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。
斯坦福机器学习视频做了很好的解释:https://class.coursera.org/ml-003/lecture/21
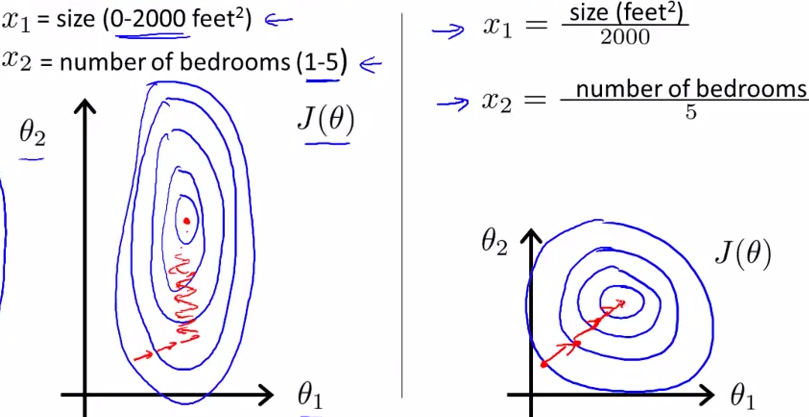
如下图所示,蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大,X1区间是[0,2000],X2区间是[1,5],其所形成的等高线非常尖。当使用梯度下降法寻求最优解时,很有可能走“之字型”路线(垂直等高线走),从而导致需要迭代很多次才能收敛;
而右图对两个原始特征进行了归一化,其对应的等高线显得很圆,在梯度下降进行求解时能较快的收敛。
因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。
正则化
正则化就是对最小化经验误差函数上加约束,这样的约束可以解释为先验知识(正则化参数等价于对参数引入先验分布)。约束有引导作用,在优化误差函数的时候倾向于选择满足约束的梯度减少的方向,使最终的解倾向于符合先验知识(如一般的l-norm先验,表示原问题更可能是比较简单的,这样的优化倾向于产生参数值量级小的解,一般对应于稀疏参数的平滑解)
正则化是针对过拟合而提出的,以为在求解模型最优的是一般优化最小的经验风险,现在在该经验风险上加入模型复杂度这一项(正则化项是模型参数向量的范数),并使用一个rate比率来权衡模型复杂度与以往经验风险的权重,如果模型复杂度越高,结构化的经验风险会越大,现在的目标就变为了结构经验风险的最优化,可以防止模型训练过度复杂,有效的降低过拟合的风险。
LP范数
范数简单可以理解为用来表征向量空间中的距离,而距离的定义很抽象,只要满足非负、自反、三角不等式就可以称之为距离。
LP范数不是一个范数,而是一组范数,其定义如下:
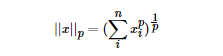
L1范数
根据LP范数的定义我们可以很轻松的得到L1范数的数学形式:
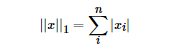
通过上式可以看到,L1范数就是向量各元素的绝对值之和,也被称为是"稀疏规则算子"(Lasso regularization)。那么问题来了,为什么我们希望稀疏化?稀疏化有很多好处,最直接的两个:
-
特征选择
-
可解释性
L2范数
L2范数是最熟悉的,它就是欧几里得距离,公式如下:

L2范数有很多名称,有人把它的回归叫“岭回归”(Ridge Regression),也有人叫它“权值衰减”(Weight Decay)。以L2范数作为正则项可以得到稠密解,即每个特征对应的参数ww都很小,接近于0但是不为0;此外,L2范数作为正则化项,可以防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
L1范数和L2范数的区别
引入PRML一个经典的图来说明下L1和L2范数的区别,如下图所示:
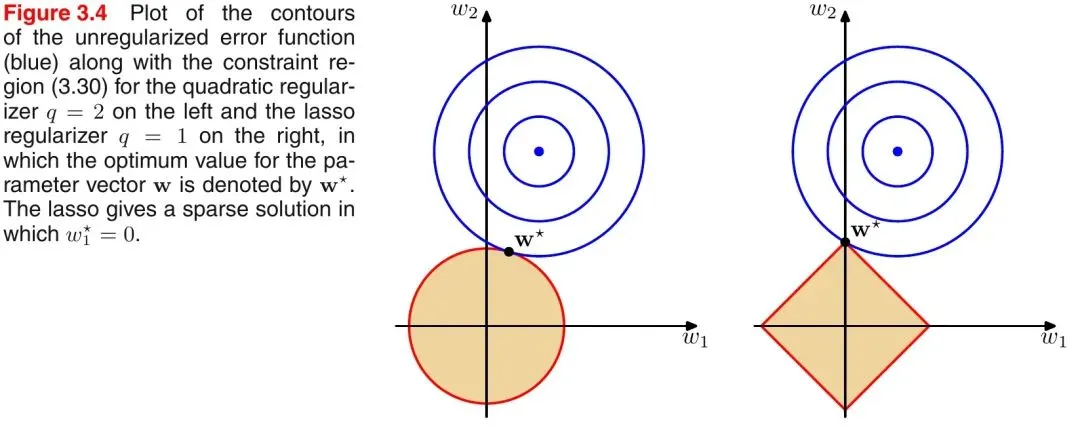
如上图所示,蓝色的圆圈表示问题可能的解范围,橘色的表示正则项可能的解范围。而整个目标函数(原问题+正则项)有解当且仅当两个解范围相切。从上图可以很容易地看出,由于L2范数解范围是圆,所以相切的点有很大可能不在坐标轴上,而由于L1范数是菱形(顶点是凸出来的),其相切的点更可能在坐标轴上,而坐标轴上的点有一个特点,其只有一个坐标分量不为零,其他坐标分量为零,即是稀疏的。所以有如下结论,L1范数可以导致稀疏解,L2范数导致稠密解。
从贝叶斯先验的角度看,当训练一个模型时,仅依靠当前的训练数据集是不够的,为了实现更好的泛化能力,往往需要加入先验项,而加入正则项相当于加入了一种先验。
-
L1范数相当于加入了一个Laplacean先验;
- L2范数相当于加入了一个Gaussian先验。

