硬币找零问题

假如现在有四种硬币类型：1角，2角，5角和1元。

你现在是超市收银员，老板要求你每次都使用最少的硬币给用户找零。

例如，用户需要找零6角，你需要找给他 一个5角 + 一个1角，这样只用到2个硬币，而不是找给他 六个1角 或者 三个2角。

面对这样的问题我们该如何思考呢？

假如当前已经选择了 i-1 枚硬币，当选择下一枚硬币 i 的时候，面对下面两种情况：

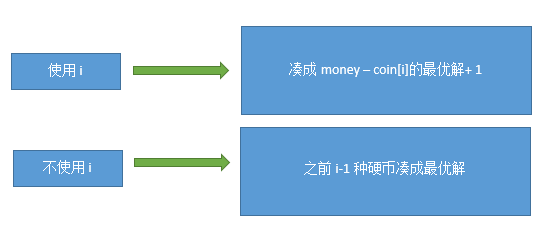
面对这两种选择我们需要做的就是选择其中的最优解。

下面以找零6角为例进行一下推算。

找零1角，可供选择的硬币为1角，那此时的最优解在选择这1角硬币和不选择这1角硬币中。

情况一：如果选择这1角硬币，这意味着需要的硬币数量 = （（找零1角 - 当前硬币金额 ）所需要的硬币数量 ）+ 1

找零1角 - 当前硬币金额 = 1 -1 = 0，而找零0角需要的硬币数量为0，所以第一种情况需要的硬币数量 = 0 + 1 = 1

情况二：如果不选择这枚硬币，这意味着需要的硬币数量 = 之前 1 - 1 = 0 种硬币找零1角的最有解。

我们知道如果硬币种类为0，我们是无法进行找零的，也就是需要找零的硬币为无穷大。

显然情况一需要的硬币数量更少。此时的最优解为1。

同理我们可以推论出后面的结果。下图显示了这个推算过程。

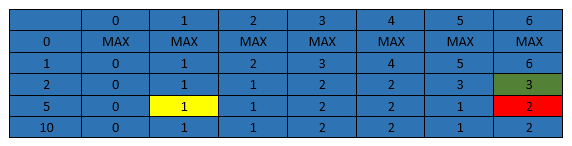
如上推算所示，我们在推演时需要考虑一些边界条件：

1、如果当前没有硬币，是无法找零的，也就是无论多少硬币都无法找零。

2、如果需要找零的金额为0，那这时候也需要找零。

3、如果需要找零的金额数量小于硬币的面额，那这枚硬币就不需要使用。比如找零金额为6角，那1元的硬币肯定是用不着的。

1、2 两个边界条件在找零钱前应该是默认成立的，所以在编写程序的时候需要将它们设置为初始条件。

边界条件3则是在我们找零过程中需要进行判断的，在编程时候应该写在找零程序中。

好了，说了这么多，还是直接上代码方便快捷= =

package com.lkb.dp.problems;

import java.util.Arrays;

/**
 * @Description 硬币找零问题
 * 假设只有 1角，2角，5角，1元的硬币，
 * 在超市结账时，如果需要找零钱，收银员希望将最少的硬币数找给顾客。那么，给定需要找的零钱数目，如何求得最少的硬币数呢？
 * @Author lkb
 * @CreateDate: 2019/6/1
 */
public class ChargeProblem {

    public static void main(String[] args) {
        int[] coinsValues = {1,2,5,10};
        Arrays.sort(coinsValues);
        int n = 6;
        int minCoinsNumber = charge(coinsValues, n);
        System.out.println(minCoinsNumber);
    }


    /**
     * 功能描述: 硬币找零问题
     * @author lkb
     * @date 2019/6/1
     * @param
     * @return int
     */
    public static int charge(int[] coinKind, int money){
        //这个数组保存最优解
        //例如  value[2][5] 表示 使用 coinKind[0] coinKind[1] coinKind[2] 找零 money = 5 的最优解
        int[][] value = new int[coinKind.length+1][money+1];

        //边界条件1：如果硬币类型为0，则永远找不到合适的硬币找零 、
        // 这里设置为最大值是因为我们后续比较使用
        for(int i=0; i<=money; i++){
            value[0][i] = Integer.MAX_VALUE;
        }
        //边界条件2：如果钱为0，则永远找不到合适的硬币找零
        for(int i=0; i<=coinKind.length; i++){
            value[i][0] = 0;
        }

        for(int mon=1; mon<=money; mon++){
            for(int kind=1; kind<=coinKind.length; kind++){
                //边界条件2：如果硬币金额大于钱，则最优解是 上一步的最优解
                if(coinKind[kind-1] > mon){
                    value[kind][mon] = value[kind-1][mon];
                    continue;
                }

                //当前最优解分为两种情况，需要在下面两种情况选择一种解最小的情况
                //一个是使用了当前类型的硬币，value[kind][mon - coinKind[kind-1]] + 1
                // 一个是没有使用当前类型的硬币, value[kind-1][mon]
                if((value[kind][mon - coinKind[kind-1]] + 1) < value[kind-1][mon]){
                    value[kind][mon] = value[kind][mon - coinKind[kind-1]] + 1;
                }else{
                    value[kind][mon] = value[kind-1][mon];
                }
            }
        }

        return value[coinKind.length][money];
    }


}

大家也可以在这个地址下载源码，或者关注我的公众号，一起见证我的成长。