有三根柱子一次为A,B,C 现在A柱子上有3个块,按照汉诺塔规则移动到C柱子上去,打印步骤?
我们这样理解:A为原始柱,C为目标柱,B为缓冲柱
1.定义一个函数move(n,a,b,c),n为原始柱上面的块数,a为原始柱名称,b为缓冲柱,c为目标柱
def move(n,a,b,c):
pass
2.首先,我们假定原始柱上只有一个块,那就是直接从原始柱移动到目标柱,无需经过缓冲柱
def move(n,a,b,c):
if n == 1:
print(a,'-->',c)
else:
pass
3.当原始柱上不止一个块的时候,我们先将上面n-1个块移动到缓冲柱上面,此时方法中的目标柱就是缓冲柱(请注意参数位置)
def move(n,a,b,c):
if n == 1:
print(a,'-->',c)
else:
move((n-1),a,c,b)
pass
4.移动完成之后此时在三根柱子上就是原始柱上有编号n的最大块,缓冲柱上有n-1个块,我们将最大块移动到目标柱上
def move(n,a,b,c):
if n == 1:
print(a,'-->',c)
else:
move((n-1),a,c,b)
print(a,'-->',c)
pass
5.最后一步,将缓冲柱子上的n-1个块移动到目标柱上
def move(n,a,b,c):
if n == 1:
print(a,'-->',c)
else:
move((n-1),a,c,b)
print(a,'-->',c)
move((n-1),b,a,c)
方法定义以及调用过程截图如下:
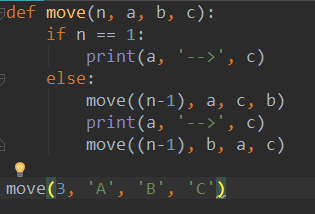
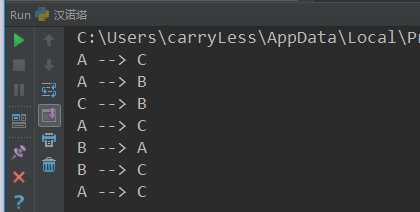
总结:整个过程中原始柱,缓冲柱,目标柱的角色不停地发生变化,当你把握住这点后,便可以轻松的使用递归调用来解决此问题