1224 Maximum Equal Frequency最大相等频率
问题描述
给出一个正整数数组 nums,请你帮忙从该数组中找出能满足下面要求的 最长 前缀,并返回其长度:
- 从前缀中
删除一个元素后,使得所剩下的每个数字的出现次数相同。
如果删除这个元素后没有剩余元素存在,仍可认为每个数字都具有相同的出现次数(也就是 0 次)。
- 示例 1:
输入:nums = [2,2,1,1,5,3,3,5]
输出:7
解释:对于长度为 7 的子数组 [2,2,1,1,5,3,3],如果我们从中删去 nums[4]=5,就可以得到 [2,2,1,1,3,3],里面每个数字都出现了两次。
- 示例 2:
输入:nums = [1,1,1,2,2,2,3,3,3,4,4,4,5]
输出:13
- 示例 3:
输入:nums = [1,1,1,2,2,2]
输出:5
- 示例 4:
输入:nums = [10,2,8,9,3,8,1,5,2,3,7,6]
输出:8
- 提示:
2 <= nums.length <= 10^51 <= nums[i] <= 10^5
思路
- 读题
前缀: 前n个元素
符合条件: 元素频次都相同, 只有一个不同
找规律
四种情况:
- 数字有两种分类, 第一类频次相等, 第二类比第一类频次多1, 并且第二类只有一个数字 --> [1,1,1,2,2,3,3]
- 数字有两种分类, 第一类频次相等, 第二类频次为1, 并且第二类只有一个数字 --> [1,1,2,2,3]
- 数字只有一类, 全重复 --> [1,1,1,1]
- 数字只有一类, 全不重复 --> [1,2,3,4]
记录下数字出现频次和出现频次的出现频次
- 示例: nums = [2,2,1,1,5,3,3,5]
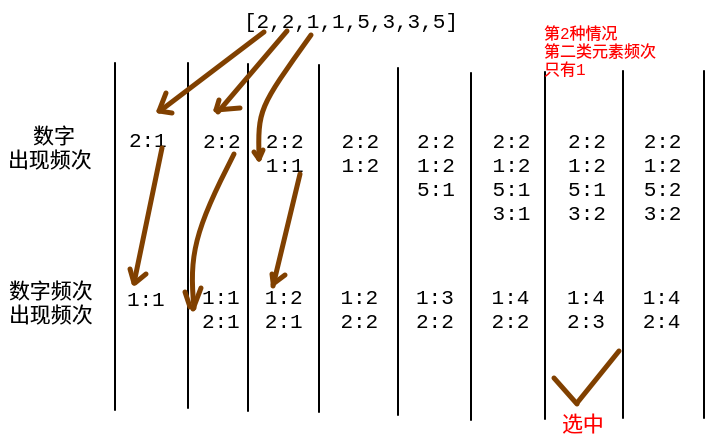
代码实现
找规律 多情况分析
class Solution {
/**
* 数据量最大界限
*/
private final static int SIZE = (int) 1e5 + 50;
public int maxEqualFreq(int[] nums) {
// freq of number 出现数字的频次
int[] freqOfNum = new int[SIZE];
// freq of number's freq 出现数字频次的频次
int[] freqOfFreq = new int[SIZE];
// maxFreq 数字出现频次的最大值
int maxFreq = Integer.MIN_VALUE, ans = 0;
/*
* 四种情况:
* 1. 数字有两种分类, 第一类频次相等, 第二类比第一类频次多1, 并且第二类只有一个数字 --> [1,1,1,2,2,3,3]
* 2. 数字有两种分类, 第一类频次相等, 第二类频次为1, 并且第二类只有一个数字 --> [1,1,2,2,3]
* 3. 数字只有一类, 全重复 --> [1,1,1,1]
* 4. 数字只有一类, 全不重复 --> [1,2,3,4]
*/
for (int i = 0; i < nums.length; i++) {
freqOfNum[nums[i]]++;
freqOfFreq[freqOfNum[nums[i]]]++;
maxFreq = Math.max(freqOfNum[nums[i]], maxFreq);
// 第一种情况: 最高频次maxFreq出现数为1, 并且次高频次(maxFreq-1)出现数*其频次==i
// --> [1,1,1,2,2,3,3] --> {maxFreq:3(1), fof[2]:3, fof[3]:1, i:6}
boolean one = (freqOfFreq[maxFreq] == 1) && (freqOfFreq[maxFreq - 1] * (maxFreq - 1) + 1 == i + 1);
// 第二种情况: 最高频次maxFreq出现数*其频次==i
// --> [1,1,2,2,3] --> {maxFreq:2, fof[2]:2, i=4}
boolean two = freqOfFreq[maxFreq] * maxFreq + 1 == i + 1;
// 第三种情况: 最高频次maxFreq出现数==1 --> [1,1,1,1] --> {maxFreq:4, fof[4]:1}
// 与第一种情况合并
boolean thr = freqOfFreq[maxFreq] == 1;
if (one || two) {
ans = i + 1;
}
}
// 第四种情况: 最高频次maxFreq==1 --> [1,2,3,4] --> {maxFreq:1, fof[1]:4}
boolean four = maxFreq == 1;
if (four) {
return nums.length;
}
return ans;
}
}
参考资源
第 157 场周赛 全球排名
java题解,让一眼就看懂的算法!算是对 @杨添伦 算法的补充
C++,O(n),考虑四种情况