本代码参考自: https://github.com/lawlite19/MachineLearning_Python/blob/master/K-Means/K-Menas.py
1. 初始化类中心,从样本中随机选取K个点作为初始的聚类中心点
def kMeansInitCentroids(X,K):
m = X.shape[0]
m_arr = np.arange(0,m) # 生成0-m-1
centroids = np.zeros((K,X.shape[1]))
np.random.shuffle(m_arr) # 打乱m_arr顺序
rand_indices = m_arr[:K] # 取前K个
centroids = X[rand_indices,:]
return centroids
2. 找出每个样本离哪一个类中心的距离最近,并返回
def findClosestCentroids(x,inital_centroids):
m = x.shape[0] #样本的个数
k = inital_centroids.shape[0] #类别的数目
dis = np.zeros((m,k)) # 存储每个点到k个类的距离
idx = np.zeros((m,1)) # 要返回的每条数据属于哪个类别
"""计算每个点到每个类的中心的距离"""
for i in range(m):
for j in range(k):
dis[i,j] = np.dot((x[i,:] - inital_centroids[j,:]).reshape(1,-1),
(x[i,:] - inital_centroids[j,:]).reshape(-1,1))
'''返回dis每一行的最小值对应的列号,即为对应的类别
- np.min(dis, axis=1) 返回每一行的最小值
- np.where(dis == np.min(dis, axis=1).reshape(-1,1)) 返回对应最小值的坐标
- 注意:可能最小值对应的坐标有多个,where都会找出来,所以返回时返回前m个需要的即可(因为对于多个最小值,
属于哪个类别都可以)
'''
dummy,idx = np.where(dis == np.min(dis,axis=1).reshape(-1,1))
return idx[0:dis.shape[0]]
3. 更新类中心
def computerCentroids(x,idx,k):
n = x.shape[1] #每个样本的维度
centroids = np.zeros((k,n)) #定义每个中心点的形状,其中维度和每个样本的维度一样
for i in range(k):
# 索引要是一维的, axis=0为每一列,idx==i一次找出属于哪一类的,然后计算均值
centroids[i,:] = np.mean(x[np.ravel(idx==i),:],axis=0).reshape(1,-1)
return centroids
4. K-Means算法实现
def runKMeans(x,initial_centroids,max_iters,plot_process):
m,n = x.shape #样本的个数和维度
k = initial_centroids.shape[0] #聚类的类数
centroids = initial_centroids #记录当前类别的中心
previous_centroids = centroids #记录上一次类别的中心
idx = np.zeros((m,1)) #每条数据属于哪个类
for i in range(max_iters):
print("迭代计算次数:%d"%(i+1))
idx = findClosestCentroids(x,centroids)
if plot_process: # 如果绘制图像
plt = plotProcessKMeans(X,centroids,previous_centroids,idx) # 画聚类中心的移动过程
previous_centroids = centroids # 重置
plt.show()
centroids = computerCentroids(x,idx,k) #重新计算类中心
return centroids,idx #返回聚类中心和数据属于哪个类别
5. 绘制聚类中心的移动过程
def plotProcessKMeans(X,centroids,previous_centroids,idx):
for i in range(len(idx)):
if idx[i] == 0:
plt.scatter(X[i,0], X[i,1],c="r") # 原数据的散点图 二维形式
elif idx[i] == 1:
plt.scatter(X[i,0],X[i,1],c="b")
else:
plt.scatter(X[i,0],X[i,1],c="g")
plt.plot(previous_centroids[:,0],previous_centroids[:,1],'rx',markersize=10,linewidth=5.0) # 上一次聚类中心
plt.plot(centroids[:,0],centroids[:,1],'rx',markersize=10,linewidth=5.0) # 当前聚类中心
for j in range(centroids.shape[0]): # 遍历每个类,画类中心的移动直线
p1 = centroids[j,:]
p2 = previous_centroids[j,:]
plt.plot([p1[0],p2[0]],[p1[1],p2[1]],"->",linewidth=2.0)
return plt
6. 主程序实现
if __name__ == "__main__":
print("聚类过程展示....
")
data = spio.loadmat("./data/data.mat")
X = data['X']
K = 3
initial_centroids = kMeansInitCentroids(X,K)
max_iters = 10
runKMeans(X,initial_centroids,max_iters,True)
7. 结果
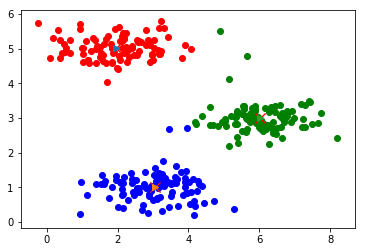
聚类过程展示.... 迭代计算次数:1
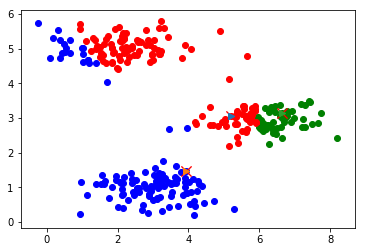
迭代计算次数:2
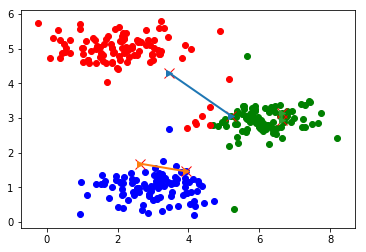
迭代计算次数:3
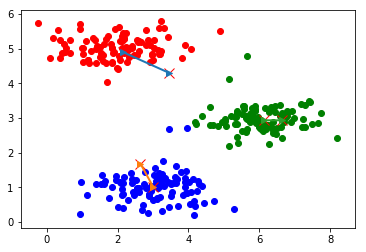
迭代计算次数:4
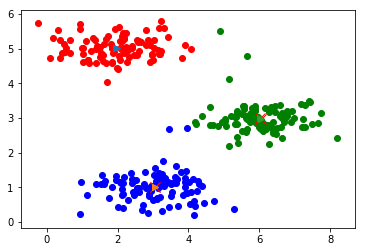
迭代计算次数:5
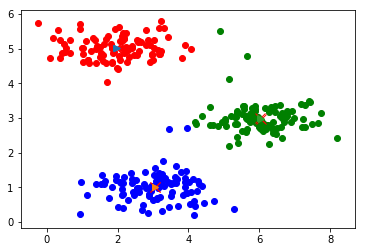
迭代计算次数:6
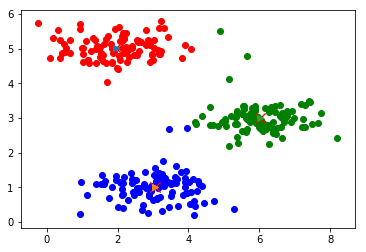
迭代计算次数:7
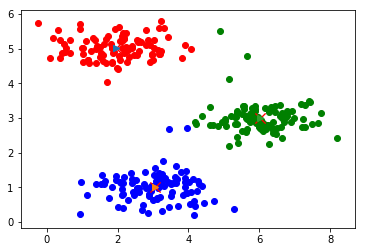
迭代计算次数:8
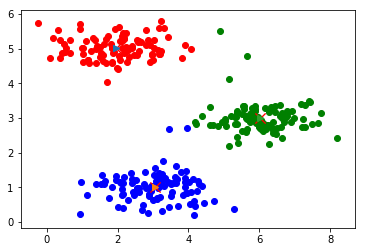
迭代计算次数:9
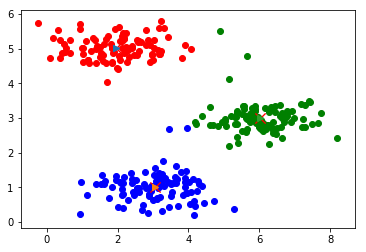
迭代计算次数:10