参考链接：http://www.dzkbw.com/books/rjb/shuxue/xgbx4/
第一章 三角函数
1.1任意角和弧度制
正角、负角和零角；
我们常在直角坐标系内讨论角，角的顶点与原点重合，角的始边与x轴的非负半轴重合；
角的终边在第几象限，我们就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限；
角的度量：角度制、弧度制；
弧度制：把长度等于半径长的弧所对的圆心角叫做1弧度的角；1rad；
180°=π rad； π=3.14；
1.2任意角的三角函数；
sin2a+cos2a=1；；；正弦 sina=y/r；余弦 cosa=x/r；正切 tana=y/x；
a≠±90°，sina/cosa=tana
sinα=-sin(π+α)；
cosα=-cos(π+α)；cosα=sin(π/2-α)
tanα=tan(π+α)
sin0°=0；sin30°=1/2；sin45°=
；sin60°=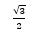
；sin90°=1；
tan0°=0； tan30°=√3/3；tan45°=1；tan60°=√3；tan90°（因为分母不能为0）；
1.4 三角函数的图像与性质
第二章 平面向量
第三章 三角恒等变换
3.1两角和与差的正弦、余弦和正切公式
cos（α-β）=cosαcosβ+sinαsinβ
cosα=sin（π/2-α）
3.2简单的三角恒等变换