今天看完soft-margin SVM就又搜了下相关的代码,最后搜到这个,第一次看懂了SVM的实现。
关于代码中cvxopt的使用,可以看下这个简单的介绍。
这里还是将代码贴在这里,里面加了自己的一下注释。
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Tue Nov 22 11:24:22 2016 4 5 @author: Administrator 6 """ 7 8 # Mathieu Blondel, September 2010 9 # License: BSD 3 clause 10 11 import numpy as np 12 from numpy import linalg 13 import cvxopt 14 import cvxopt.solvers 15 16 def linear_kernel(x1, x2): 17 return np.dot(x1, x2) 18 19 def polynomial_kernel(x, y, p=3): 20 return (1 + np.dot(x, y)) ** p 21 22 def gaussian_kernel(x, y, sigma=5.0): 23 return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2))) 24 25 class SVM(object): 26 27 def __init__(self, kernel=linear_kernel, C=None): 28 self.kernel = kernel 29 self.C = C 30 if self.C is not None: self.C = float(self.C) 31 32 def fit(self, X, y): 33 n_samples, n_features = X.shape 34 35 # Gram matrix 36 K = np.zeros((n_samples, n_samples)) 37 for i in range(n_samples): 38 for j in range(n_samples): 39 K[i,j] = self.kernel(X[i], X[j]) 40 41 P = cvxopt.matrix(np.outer(y,y) * K) 42 q = cvxopt.matrix(np.ones(n_samples) * -1) 43 A = cvxopt.matrix(y, (1,n_samples)) 44 b = cvxopt.matrix(0.0) 45 46 if self.C is None: 47 G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1)) 48 h = cvxopt.matrix(np.zeros(n_samples)) 49 else: 50 tmp1 = np.diag(np.ones(n_samples) * -1) 51 tmp2 = np.identity(n_samples) 52 G = cvxopt.matrix(np.vstack((tmp1, tmp2))) 53 tmp1 = np.zeros(n_samples) 54 tmp2 = np.ones(n_samples) * self.C 55 h = cvxopt.matrix(np.hstack((tmp1, tmp2))) 56 57 # solve QP problem 58 solution = cvxopt.solvers.qp(P, q, G, h, A, b) 59 # Lagrange multipliers 60 ''' 61 数组的flatten和ravel方法将数组变为一个一维向量(铺平数组)。 62 flatten方法总是返回一个拷贝后的副本, 63 而ravel方法只有当有必要时才返回一个拷贝后的副本(所以该方法要快得多,尤其是在大数组上进行操作时) 64 ''' 65 a = np.ravel(solution['x']) 66 # Support vectors have non zero lagrange multipliers 67 ''' 68 这里a>1e-5就将其视为非零 69 ''' 70 sv = a > 1e-5 # return a list with bool values 71 ind = np.arange(len(a))[sv] # sv's index 72 self.a = a[sv] 73 self.sv = X[sv] # sv's data 74 self.sv_y = y[sv] # sv's labels 75 print("%d support vectors out of %d points" % (len(self.a), n_samples)) 76 77 # Intercept 78 ''' 79 这里相当于对所有的支持向量求得的b取平均值 80 ''' 81 self.b = 0 82 for n in range(len(self.a)): 83 self.b += self.sv_y[n] 84 self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv]) 85 self.b /= len(self.a) 86 87 # Weight vector 88 if self.kernel == linear_kernel: 89 self.w = np.zeros(n_features) 90 for n in range(len(self.a)): 91 # linear_kernel相当于在原空间,故计算w不用映射到feature space 92 self.w += self.a[n] * self.sv_y[n] * self.sv[n] 93 else: 94 self.w = None 95 96 def project(self, X): 97 # w有值,即kernel function 是 linear_kernel,直接计算即可 98 if self.w is not None: 99 return np.dot(X, self.w) + self.b 100 # w is None --> 不是linear_kernel,w要重新计算 101 # 这里没有去计算新的w(非线性情况不用计算w),直接用kernel matrix计算预测结果 102 else: 103 y_predict = np.zeros(len(X)) 104 for i in range(len(X)): 105 s = 0 106 for a, sv_y, sv in zip(self.a, self.sv_y, self.sv): 107 s += a * sv_y * self.kernel(X[i], sv) 108 y_predict[i] = s 109 return y_predict + self.b 110 111 def predict(self, X): 112 return np.sign(self.project(X)) 113 114 if __name__ == "__main__": 115 import pylab as pl 116 117 def gen_lin_separable_data(): 118 # generate training data in the 2-d case 119 mean1 = np.array([0, 2]) 120 mean2 = np.array([2, 0]) 121 cov = np.array([[0.8, 0.6], [0.6, 0.8]]) 122 X1 = np.random.multivariate_normal(mean1, cov, 100) 123 y1 = np.ones(len(X1)) 124 X2 = np.random.multivariate_normal(mean2, cov, 100) 125 y2 = np.ones(len(X2)) * -1 126 return X1, y1, X2, y2 127 128 def gen_non_lin_separable_data(): 129 mean1 = [-1, 2] 130 mean2 = [1, -1] 131 mean3 = [4, -4] 132 mean4 = [-4, 4] 133 cov = [[1.0,0.8], [0.8, 1.0]] 134 X1 = np.random.multivariate_normal(mean1, cov, 50) 135 X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50))) 136 y1 = np.ones(len(X1)) 137 X2 = np.random.multivariate_normal(mean2, cov, 50) 138 X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50))) 139 y2 = np.ones(len(X2)) * -1 140 return X1, y1, X2, y2 141 142 def gen_lin_separable_overlap_data(): 143 # generate training data in the 2-d case 144 mean1 = np.array([0, 2]) 145 mean2 = np.array([2, 0]) 146 cov = np.array([[1.5, 1.0], [1.0, 1.5]]) 147 X1 = np.random.multivariate_normal(mean1, cov, 100) 148 y1 = np.ones(len(X1)) 149 X2 = np.random.multivariate_normal(mean2, cov, 100) 150 y2 = np.ones(len(X2)) * -1 151 return X1, y1, X2, y2 152 153 def split_train(X1, y1, X2, y2): 154 X1_train = X1[:90] 155 y1_train = y1[:90] 156 X2_train = X2[:90] 157 y2_train = y2[:90] 158 X_train = np.vstack((X1_train, X2_train)) 159 y_train = np.hstack((y1_train, y2_train)) 160 return X_train, y_train 161 162 def split_test(X1, y1, X2, y2): 163 X1_test = X1[90:] 164 y1_test = y1[90:] 165 X2_test = X2[90:] 166 y2_test = y2[90:] 167 X_test = np.vstack((X1_test, X2_test)) 168 y_test = np.hstack((y1_test, y2_test)) 169 return X_test, y_test 170 171 # 仅仅在Linears使用此函数作图,即w存在时 172 def plot_margin(X1_train, X2_train, clf): 173 def f(x, w, b, c=0): 174 # given x, return y such that [x,y] in on the line 175 # w.x + b = c 176 return (-w[0] * x - b + c) / w[1] 177 178 pl.plot(X1_train[:,0], X1_train[:,1], "ro") 179 pl.plot(X2_train[:,0], X2_train[:,1], "bo") 180 pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g") 181 182 # w.x + b = 0 183 a0 = -4; a1 = f(a0, clf.w, clf.b) 184 b0 = 4; b1 = f(b0, clf.w, clf.b) 185 pl.plot([a0,b0], [a1,b1], "k") 186 187 # w.x + b = 1 188 a0 = -4; a1 = f(a0, clf.w, clf.b, 1) 189 b0 = 4; b1 = f(b0, clf.w, clf.b, 1) 190 pl.plot([a0,b0], [a1,b1], "k--") 191 192 # w.x + b = -1 193 a0 = -4; a1 = f(a0, clf.w, clf.b, -1) 194 b0 = 4; b1 = f(b0, clf.w, clf.b, -1) 195 pl.plot([a0,b0], [a1,b1], "k--") 196 197 pl.axis("tight") 198 pl.show() 199 200 def plot_contour(X1_train, X2_train, clf): 201 # 作training sample数据点的图 202 pl.plot(X1_train[:,0], X1_train[:,1], "ro") 203 pl.plot(X2_train[:,0], X2_train[:,1], "bo") 204 # 做support vectors 的图 205 pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g") 206 X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50)) 207 X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))]) 208 Z = clf.project(X).reshape(X1.shape) 209 # pl.contour做等值线图 210 pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower') 211 pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower') 212 pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower') 213 214 pl.axis("tight") 215 pl.show() 216 217 def test_linear(): 218 X1, y1, X2, y2 = gen_lin_separable_data() 219 X_train, y_train = split_train(X1, y1, X2, y2) 220 X_test, y_test = split_test(X1, y1, X2, y2) 221 222 clf = SVM() 223 clf.fit(X_train, y_train) 224 225 y_predict = clf.predict(X_test) 226 correct = np.sum(y_predict == y_test) 227 print("%d out of %d predictions correct" % (correct, len(y_predict))) 228 229 plot_margin(X_train[y_train==1], X_train[y_train==-1], clf) 230 231 def test_non_linear(): 232 X1, y1, X2, y2 = gen_non_lin_separable_data() 233 X_train, y_train = split_train(X1, y1, X2, y2) 234 X_test, y_test = split_test(X1, y1, X2, y2) 235 236 clf = SVM(gaussian_kernel) 237 clf.fit(X_train, y_train) 238 239 y_predict = clf.predict(X_test) 240 correct = np.sum(y_predict == y_test) 241 print("%d out of %d predictions correct" % (correct, len(y_predict))) 242 243 plot_contour(X_train[y_train==1], X_train[y_train==-1], clf) 244 245 def test_soft(): 246 X1, y1, X2, y2 = gen_lin_separable_overlap_data() 247 X_train, y_train = split_train(X1, y1, X2, y2) 248 X_test, y_test = split_test(X1, y1, X2, y2) 249 250 clf = SVM(C=0.1) 251 clf.fit(X_train, y_train) 252 253 y_predict = clf.predict(X_test) 254 correct = np.sum(y_predict == y_test) 255 print("%d out of %d predictions correct" % (correct, len(y_predict))) 256 257 plot_contour(X_train[y_train==1], X_train[y_train==-1], clf) 258 259 # test_soft() 260 # test_linear() 261 test_non_linear()
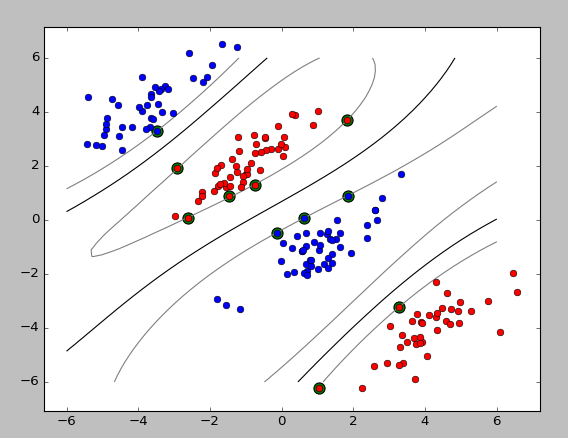
运行结果: