 Problem 1759 Super A^B mod C
Problem 1759 Super A^B mod CAccept: 1368 Submit: 4639
Time Limit: 1000 mSec Memory Limit : 32768 KB
 Problem Description
Problem Description
Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).
 Input
Input
There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.
 Output
Output
For each testcase, output an integer, denotes the result of A^B mod C.
 Sample Input
Sample Input
3 2 4
2 10 1000
 Sample Output
Sample Output
1
24
题意:求(a^b)%c的值,由于是mod一个数,数据范围又非常大,我们非常容易想到循环节这个东西
那么我们就可以根据一个数学公式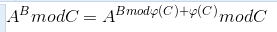
 View Code
View Code
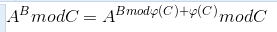
求出c的欧拉函数,最后再求快速幂,就可以得到long long范围内的结果了
tips:FOJ不支持万能头文件和%lld
http://acm.fzu.edu.cn/problem.php?pid=1759

#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> using namespace std; const int maxn=1e6+5; typedef long long ll; char str[maxn]; int phi(int n){ int rea=n; for(int i=2;i*i<=n;i++){ if(n%i==0){ rea=rea-rea/i; while(n%i==0) n/=i; } } if(n>1) rea=rea-rea/n; return rea; } ll multi(ll a,ll b,ll m){ ll ans=0; a%=m; while(b){ if(b&1){ ans=(ans+a)%m; b--; } b>>=1; a=(a+a)%m; } return ans; } ll quick_mod(ll a,ll b,ll m){ ll ans=1; a%=m; while(b){ if(b&1){ ans=multi(ans,a,m); b--; } b>>=1; a=multi(a,a,m); } return ans; } void solve(ll a,char str[],ll c){ ll len=strlen(str); ll ans=0; ll p=phi(c); if(len<=15){ for(int i=0;i<len;i++){ ans=ans*10+str[i]-'0'; } }else{ for(int i=0;i<len;i++){ ans=ans*10+str[i]-'0'; ans%=p; } ans+=p; } printf("%I64d ",quick_mod(a,ans,c)); } int main(){ ll a,c; while(~scanf("%I64d%s%I64d",&a,str,&c)){ solve(a,str,c); } return 0; }
