-
前置芝士:
欧拉函数(φ(p)):即指在[1,p-1][1,p−1]中与p互质的数的个数,特别的,φ(1)=1。
- 单数值求欧拉函数:(时间复杂度O(√n))
-
 View Code
View Code1 int euler(int n){ //返回euler(n) 2 int res=n,a=n; 3 for(int i=2;i*i<=a;i++) 4 if(a%i==0){ 5 res=res/i*(i-1); 6 while(a%i==0) a/=i; 7 } 8 } 9 if(a>1) res=res/a*(a-1); 10 return res; 11 }
- 线性筛欧拉函数:(时间复杂度O(n))
-
 View Code
View Code1 void getphi(){ 2 phi[1]=1; 3 for(i=2;i<=N;i++){//相当于分解质因式的逆过程 4 if(!mark[i]){ 5 prime[++tot]=i;//筛素数的时候首先会判断i是否是素数。 6 phi[i]=i-1;//当 i 是素数时 phi[i]=i-1 7 } 8 for(j=1;j<=tot;j++){ 9 if(i*prime[j]>N) break; 10 mark[i*prime[j]]=1;//确定i*prime[j]不是素数 11 if(i%prime[j]==0){//接着我们会看prime[j]是否是i的约数 12 phi[i*prime[j]]=phi[i]*prime[j]; 13 break; 14 } 15 else phi[i*prime[j]]=phi[i]*(prime[j]-1);//其实这里prime[j]-1就是phi[prime[j]],利用了欧拉函数的积性 16 } 17 } 18 }
-
Eg:通式:

欧拉定理
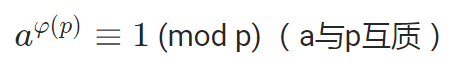
引入概念
基本概念——完全剩余系:从模n的每个剩余类中各取一个数,得到一个由0到n-1,n个数组成的集合,叫做模n的一个完全剩余系。
就是说刚好取遍所有mod p意义下余数的任意一个数的集合。
引入引理



下面是对于欧拉定理的证明

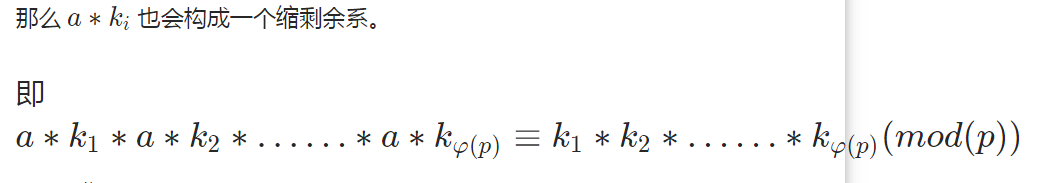
左右同时约分可得:
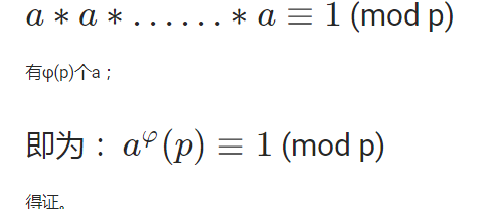

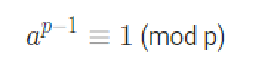
扩展欧拉定理及其证明

证明: 附链接[(https://blog.csdn.net/can919/article/details/82318115)]

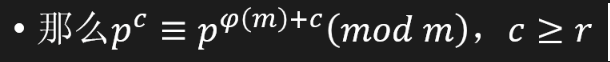
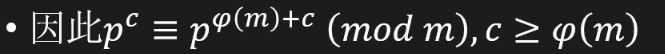
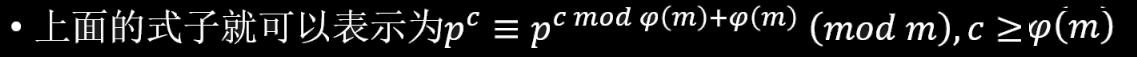
对于质数的幂在mod(m)的意义下:
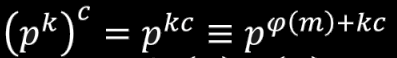 又
又
所以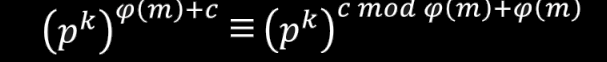
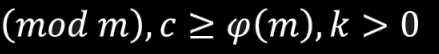
综述:
得证。
-
下面是 扩展欧拉定理(P5091)模板代码(读入时根据扩展欧拉定理优化取模)
-
 View Code
View Code1 #pragma GCC optimize(2) 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<iostream> 6 #include<cctype> 7 #include<ctime> 8 #include<cstdlib> 9 #include<map> 10 #include<algorithm> 11 12 using namespace std; 13 14 #define ll long long 15 16 ll a,m,b; 17 18 ll power(ll a,ll b,ll m); 19 inline ll read(); 20 inline ll read_(ll m); 21 inline void write(ll x); 22 ll euler(ll n); 23 24 int main(){ 25 a=read();m=read(); 26 b=read_(euler(m)); 27 write(power(a,b,m)); 28 } 29 30 ll power(ll a,ll b,ll m){ 31 ll ret=1; 32 while(b){ 33 if(b&1) ret=ret*a%m; 34 a=a*a%m; 35 b>>=1; 36 } 37 return ret; 38 } 39 40 inline ll read(){ 41 ll a=1,b=0;char t; 42 while(t<'0'||t>'9'){ 43 if(t=='-') a=-1; 44 t=getchar(); 45 } 46 while(t>='0'&&t<='9') b=b*10-'0'+t,t=getchar(); 47 return a*b; 48 } 49 50 inline ll read_(ll m){ 51 bool flag=0; 52 ll y=0;char t=getchar(); 53 while(t<'0'||t>'9') t=getchar(); 54 while(t>='0'&&t<='9'){ 55 y=y*10-'0'+t; 56 if(y>=m) flag=1; 57 y%=m; 58 t=getchar(); 59 } 60 if(flag) return y+m; 61 return y; 62 } 63 64 inline void write(ll x){ 65 ll fig[33],top=0; 66 if(!x) putchar('0'); 67 while(x) fig[++top]=x%10,x/=10; 68 while(top) putchar(fig[top--]+'0'); 69 } 70 71 ll euler(ll n){ 72 ll res=n,a=n; 73 for(int i=2;i*i<=a;i++) 74 if(!(a%i)){ 75 res=res/i*(i-1); 76 while(!(a%i)) a/=i; 77 } 78 if(a>1) res=res/a*(a-1); 79 return res; 80 }
