1. 读写文件
# 写:函数将数据a存储到test.txt文件中
np.savetxt('test.txt', a)
# 读:表示读取test.csv文件
x, y = np.loadtxt('test.csv',
delimiter=',', # 分隔符
usecols=(6,7), # 取哪几列数据
unpack=True) # 分拆存储不同列的数据,即分别将第6列与第7列数据赋值给变量x,y
2. 内建向量/矩阵
-
zeros(shape)
np.zeros((2, 3)) # output: array([[ 0., 0., 0.], [ 0., 0., 0.]]) -
ones(shape)
-
arange(n)
arange函数类似于python的range函数,通过指定开始值、终值和步长来创建一维数组,注意数组不包括终值:
np.arange(2, 10, dtype=np.float) # [ 2. 3. 4. 5. 6. 7. 8. 9.] -
linspace()
linspace函数通过指定开始值、终值和元素个数来创建一维数组,可以通过endpoint关键字指定是否包括终值,缺省设置是包括终值:
np.linspace(1., 4., 6) # array([ 1., 1.6, 2.2, 2.8, 3.4, 4. ]) -
logspace()
logspace函数和linspace类似,不过它创建等比数列,下面的例子产生1(100)到100(102)、有20个元素的等比数列:

-
random.random()
3. 切片操作

索引和切片功能在操作矩阵时变得更加有用。可以在不同维度上使用索引操作来对数据进行切片。
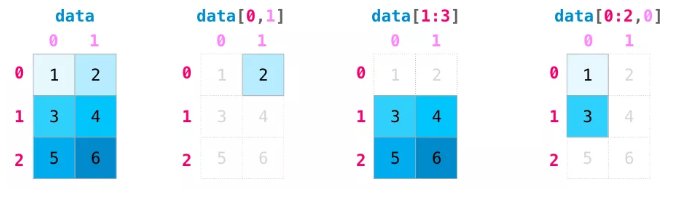
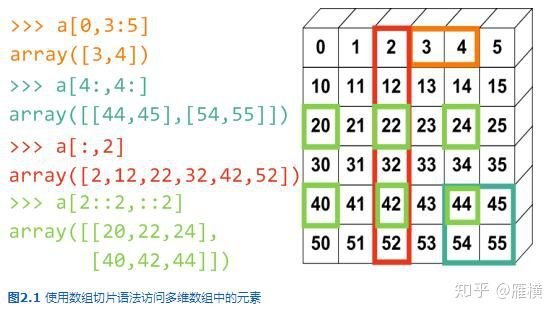
你也许会对如何创建a这样的数组感到好奇,数组a实际上是一个加法表,纵轴的值为0, 10, 20, 30, 40, 50;横轴的值为0, 1, 2, 3, 4, 5。纵轴的每个元素都和横轴的每个元素求和,就得到图中所示的数组a。
np.arange(0, 60, 10).reshape(-1, 1) + np.arange(0, 6)
array([[ 0, 1, 2, 3, 4, 5],
[10, 11, 12, 13, 14, 15],
[20, 21, 22, 23, 24, 25],
[30, 31, 32, 33, 34, 35],
[40, 41, 42, 43, 44, 45],
[50, 51, 52, 53, 54, 55]])
多维数组同样也可以使用整数序列和布尔数组进行存取。

-
a[(0,1,2,3,4),(1,2,3,4,5)]
用于存取数组的下标和仍然是一个有两个元素的组元,组元中的每个元素都是整数序列,分别对应数组的第0轴和第1轴。从两个序列的对应位置取出两个整数组成 下标: a[0,1], a[1,2], ..., a[4,5]。
-
a[3:, [0, 2, 5]]
下标中的第0轴是一个范围,它选取第3行之后的所有行;第1轴是整数序列,它选取第0, 2, 5三列。
-
a[mask, 2]
下标的第0轴是一个布尔数组,它选取第0,2,5行;第1轴是一个整数,选取第2列。
4. 聚合函数
4.1. 向量
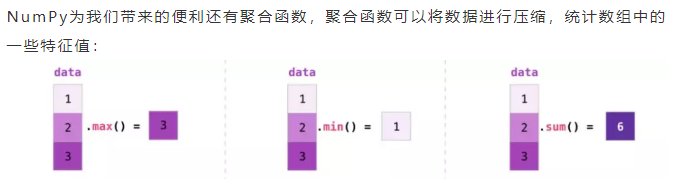
除了min,max和sum等函数,还有mean(均值),prod(数据乘法)计算所有元素的乘积,std(标准差),等等。上面的所有例子都在一个维度上处理向量。除此之外,NumPy之美的一个关键之处是它能够将之前所看到的所有函数应用到任意维度上。
4.2. 矩阵
我们可以像聚合向量一样聚合矩阵:

注意:axis的用法并不等同于 row, column... 的顺序。
5. 矩阵的转置和重构

重构:只需将矩阵所需的新维度传入即可。也可以传入-1,NumPy可以根据你的矩阵推断出正确的维度:
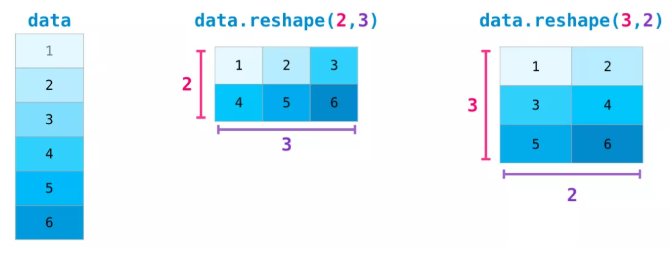

注意:数组a和d其实共享数据存储内存区域,因此修改其中任意一个数组的元素都会同时修改另外一个数组的内容:

6. 常用操作API
#加权平均,v作为权重参数
np.average(c, weights=v)
#算术平均
np.mean(c)
#取值范围
np.max(c)
np.min(c)
#ptp函数返回最大值与最小值之间的差值
np.ptp(c)
#median函数返回中位数
np.median(c)
#var方差
np.var(c)
#diff函数返回一个由相邻数组元素的差值构成的数组
np.diff(c)
#std函数计算标准差
np.std(c)
#where函数根据指定的条件返回所有满足条件的数组元素的索引值
idx = np.where(c>6)
# take函数按照索引值从数组中取出相应的元素,np.take(c,np.where(c>6))
data = np.take(idx)
#argmin返回是c数组中最小元素的索引值,argmax返回最大值索引值
np.argmin(c)
np.argmax(c)
#maximum函数可返回多个数组里的各最大值
np.maximum(a, b, c)
#同理minximum返回最小值
#exp函数可计算每个数组元素的指数
np.exp(x)
#linspace(s, e, [n])函数起始s, 终止e,个数n(可选),返回一个元素值在指定的范围内均匀分布的数组
np.linspace(-1, 0, 5)
7. 应用实例
7.1. 生成向量、矩阵
vec = np.linspace(-2,2,100) # 产生直线数据
myZero = np.zeros([3,5]) # 3*5的全0矩阵
myZero = np.ones([3,5]) # 3*5的全1矩阵
myRand = np.random.rand(3,4) # 3行4列的0~1之间的随机数矩阵
myEye = np.eye(3) # 3*3的矩阵
7.2. 数组数据的提取与过滤
mymatrix.shape
--> 矩阵的行数和列数: (3, 4)
mymatrix1[0] # 按行切片
--> 按行切片: [[1 2 3]]
mymatrix1.T[0] # 按列切片
--> 按列切片: [[1 4 7]]
mymatrix = mymatrix1.copy() # 矩阵的复制
mymatrix < mymatrix1.T # 按位比较
--> 矩阵元素的比较:
[[False True True]
[False False True]
[False False False]]
-
clip()
将所有比给定最大值还大的元素全部设为给定的最大值,而所有比给定最小值还小的元素全部设定为给定的最小值。
a = np.arange(5) a.clip(1,3) # 输出: array([1, 1, 2, 3, 3]) -
trim_zeros():去掉一维数组中开头和末尾为0的元素
-
compress()
返回一个根据给定条件筛选后的数组
a = np.arange(5) a.compress(a > 2) # array([3, 4])
7.3. 四则运算
newMat = myOnes + myEye # 元素的加和减(条件是矩阵的行数和列数必须相同)
newMat = 3 * matrix # 矩阵乘常数
newMat = matrix.sum() # 矩阵全部元素求和
newMat = power(matrix1, 2) # 矩阵各元素的n次幂:n=2
'''
矩阵各元素的积:矩阵的点乘同维对应元素的相乘。
当矩阵的维度不同时,会根据一定的广播将维数扩
充到一致的形式
'''
matrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
matrix2 = 1.5 * ones([3,3])
newMat = multiply(matrix1, matrix2)
--> 输出结果:
[[ 1.5 3. 4.5]
[ 6. 7.5 9. ]
[ 10.5 12. 13.5]]
# 矩阵乘矩阵
matrix1 = mat([[1,2,3],[4,5,6],[7,8,9]])
matrix2 = mat([[1],[2],[3]])
newMat = matrix1 * matrix2
--> 输出结果:
[[14]
[32]
[50]]
7.3.1. multiply()
对应位置相乘(同 * 星乘)。如有必要,会进行 broadcast 之后(两者有相同的维数)再进行处理。
A = np.arange(1,5).reshape(2,2)
B = np.arange(0,4).reshape(2,2)
np.multiply(A,B) # array([[0, 2],[6, 12]])
对于矩阵,与ndarray处理相同
np.multiply(np.mat(A),np.mat(B))
--> matrix([[ 0, 2],
[ 6, 12]])
7.3.2. 星乘(*)
ndarray: 星乘表示矩阵内各对应位置相乘(同 np.multiplyt() )。
a = numpy.array([[1,2],
[3,4]])
b = numpy.array([[5,6],
[7,8]])
a * b
>>> array([[ 5, 12],
[21, 32]])
matrix: 执行矩阵乘法运算(内积)
np.matrix(a) * np.matrix(b)
--> matrix([[19, 22],
[43, 50]])
7.3.3. 点乘(.dot)
数组秩不为1的场景
如果 a 和 b都是 1-D arrays,它的作用是计算内积。(不进行复共轭)
点乘表示求矩阵内积,二维数组称为矩阵积 mastrix product 。
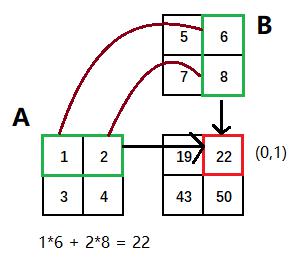
numpy.dot(a,b)
>>> array([[19, 22],
[43, 50]])
numpy.dot(b,a)
>>> array([[23, 34],
[31, 46]])
数组秩为1的场景
C = np.arange(1,4)
D = np.arange(0,3)
np.dot(C,D) #对应位置相乘,再求和: 8
7.4. 阶乘
-
prod()
a = np.arange(1,5) a.prod() # 输出: 24 -
cumprod()
a.cumprod() # array([ 1, 2, 6, 24], dtype=int32)
7.5. 判断数组数据的正负性
-
sign()
返回数组中每个元素的正负符号
c = np.linspace(-2, 2, 5) # array([-2., -1., 0., 1., 2.]) np.sign(c) # array([-1., -1., 0., 1., 1.]) -
piecewise()
来获取数组元素的正负。piecewise函数可以分段取值
np.piecewise(c, [c<-1, c>1], [-2, 1])
7.6. 矩阵的变换
a = np.arange(6).reshape(2,3) # reshape
# 矩阵的转置
newMat = matrix1.T
matrix1.transpose() # 转置(改写原矩阵)
from numpy import linalg
A = mat([[1,2,3],[4,5,6],[7,8,9]])
invA = linalg.inv(A) # 矩阵的逆
n = linalg.det(A) # 矩阵的行列式运算
n = linalg.matrix_rank(A) # 矩阵的秩
7.7. 可逆矩阵求解
A = np.mat([[1,2,4,5,7],[9,12,11,8,2],[6,4,3,2,1],[9,1,3,4,5],[0,2,3,4,1]])
b = np.mat([1, 0, 1, 0, 1])
S = linalg.solve(A, b.T)
# 输出结果:
matrix([[-0.0270936 ],
[ 1.77093596],
[-3.18472906],
[ 1.68965517],
[ 0.25369458]])
相关性
#协方差,描述两个变量共同变化趋势
c = np.cov(a,b)
#diagonal返回对角线上的元素
c.diagonal()
#trace计算矩阵的迹,即对角线上元素之和
c.trace()
#corrcoef函数计算相关系数(或者更精确地,相关系数矩阵)
np.corrcoef(a, b)
8. 附录
8.1. 从字符串读取ndarray
使用frombuffer, fromstring, fromfile等函数可以从字节序列创建数组,下面以fromstring为例。
Python的字符串实际上是字节序列,每个字符占一个字节,因此如果从字符串s创建一个8bit的整数数组的话,所得到的数组正好就是字符串中每个字符的ASCII编码:

如果从字符串s创建16bit的整数数组,那么两个相邻的字节就表示一个整数,把字节98和字节97当作一个16位的整数,它的值就是98*256+97 = 25185。可以看出内存中是以little endian(低位字节在前)方式保存数据的。
>>> np.fromstring(s, dtype='int16')
array([25185, 25699, 26213, 26727], dtype=int16)
如果把整个字符串转换为一个64位的双精度浮点数数组,那么它的值是:
>> np.fromstring(s, dtype="float")
array([8.54088322e+194])
显然这个例子没有什么意义,但是可以想象如果我们用C语言的二进制方式写了一组double类型的数值到某个文件中,那们可以从此文件读取相应的数据,并通过fromstring函数将其转换为float64类型的数组。
我们可以写一个Python的函数,它将数组下标转换为数组中对应的值,然后使用此函数创建数组:
>>> def func(i):
... return i % 4 + 1
...
>>> np.fromfunction(func, (10,))
array([1., 2., 3., 4., 1., 2., 3., 4., 1., 2.])
fromfunction函数的第一个参数为计算每个数组元素的函数,第二个参数为数组的大小(shape),因为它支持多维数组,所以第二个参数必须是一个序列,本例中用(10,)创建一个10元素的一维数组。
下面的例子创建一个二维数组表示九九乘法表,输出的数组a中的每个元素a[i, j]都等于func2(i, j):

8.2. 结构数组
在C语言中我们可以通过struct关键字定义结构类型,结构中的字段占据连续的内存空间,每个结构体占用的内存大小都相同,因此可以很容易地定义 结构数组。和C语言一样,在NumPy中也很容易对这种结构数组进行操作。只要NumPy中的结构定义和C语言中的定义相同,NumPy就可以很方便地读 取C语言的结构数组的二进制数据,转换为NumPy的结构数组。
假设我们需要定义一个结构数组,它的每个元素都有name, age和weight字段。在NumPy中可以如下定义:
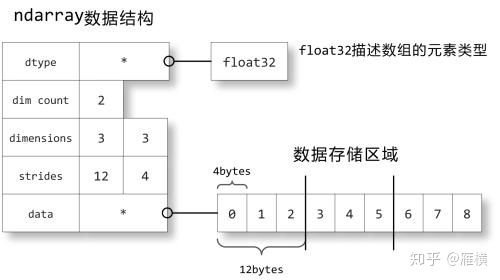
8.3. 内存结构
下面让我们来看看ndarray数组对象是如何在内存中储存的。如图2.3所示,关于数组的描述信息保存在一个数据结构中,这个结构引用两个对象:一块用于保存数据的存储区域和一个用于描述元素类型的dtype对象。