凸包

关于凸包：

概念：在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为 X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造；

简单来说：给你一个点集Q,你可以把Q中的每个点想象成一块木板上的铁钉，而点集Q的凸包就是包围了所有铁钉的一条拉紧了橡皮绳所构成的形状；

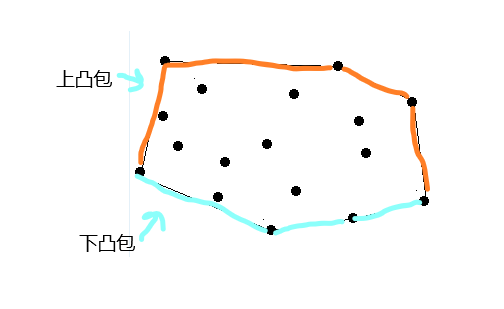
在构造凸包时，有两种情况，一种是上凸包，一种是下凸包；

在构造之前，我们需要先对这些点进行排序，按照x轴从小到大排，x相等时按照y轴从小到大排；

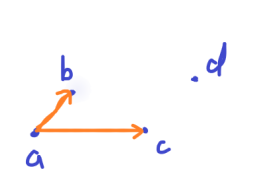
对于上凸包，我们先选中前两个点，然后判断接下来的点，如图，先确定a点和b点，然后判断c点可否加入，连接ab，ac，可以看到，ac在ab的顺时针方向，因此c点可以加进来，然后判断d点；

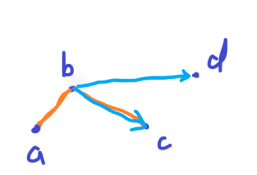
利用上面的方法，可以看到bd在bc的逆时针方向，这个时候，我们就需要把c点删除掉了，因为显然去掉c点可以使凸包的面积更大。

下凸包：

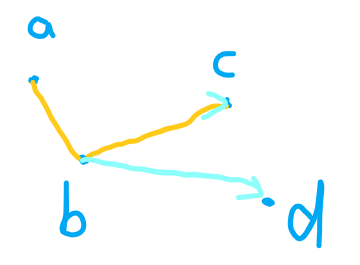
同样先选中前两个点，如图，可以看到，ac在ab的逆时针方向，这时可以把c点加入（与上凸包情况相反），接下来判断d点；

 

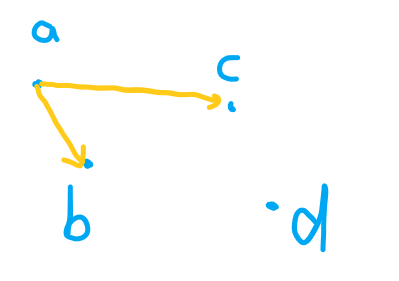
如下图，可以看到bd在bc的顺时针方向，此时删除c点选择d点可以得到更大的凸包；

构造的方法就是这样了，而对于构造时的判断，就要用到×乘的运算了；

关于×乘：

两向量 P(x1,y1),Q(x2,y2)

叉积 : P*Q = x1 * y2 - x2 * y1 ;

若P*Q>0，则P在Q的顺时针方向。

若P*Q=0，则P与Q共线，但可能同向也可能反向。

若P*Q<0，则P在Q得逆时针方向。

接下来贴一道例题

原题链接: http://acm.hdu.edu.cn/showproblem.php?pid=1392

 题目要求： 求凸包的周长

代码如下：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stack>
#include <queue>
#include <cmath>
#define ll long long
#define pi 3.1415927
using namespace std;
struct node {
double j,k;
};
node a[105],res[105];   ///数组a用来记录所有的点，数组res用来记录凸包的点
bool cmp(node x,node y)
{
    if (x.j!=y.j)
        return x.j<y.j;
    return x.k<y.k;
}
double cross(node a, node b, node c) /// × 乘
{
    return (a.j-c.j)*(b.k-c.k)-(a.k-c.k)*(b.j-c.j);
}
double dis(node a,node b)  ///计算两点距离
{
    return sqrt((a.j-b.j)*(a.j-b.j)+(a.k-b.k)*(a.k-b.k));
}
int main ()
{
    int n,m,i,t;
    while(scanf("%d",&n) )
    {
        if (n==0)
            break;
        for(i=0;i<n;++i){
            scanf("%lf %lf",&a[i].j,&a[i].k);
        }
        if (n==1)     ///n为1，2时要特判一下
        {
            printf("0.00
");
            continue;
        }
        if (n==2)
        {
            printf("%.2f
",dis(a[0],a[1]));
            continue;
        }
        sort(a,a+n,cmp);
        res[0]=a[0]; res[1]=a[1];
        t=2;
        for(i=2;i<n;++i) ///下凸包
        {
            while(t>=2 && cross(a[i],res[t-1],res[t-2])>0 )
                t--;
            res[t]=a[i];
            t++;
        }
        int p=t;
        for (i=n-2;i>=0;--i) ///上凸包
        {
            while(t>=p && cross(res[t-1],a[i],res[t-2])<0 )
                t--;
            res[t]=a[i];
            t++;
        }
        double sum=0;
        t--;
        for(i=0;i<t;++i)
            sum+=dis(res[i],res[i+1]);
        printf("%.2f
",sum);
    }
    return 0;
}