Codeforces Round #363 (Div. 2)D. Fix a Tree(并查集)

D. Fix a Tree

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A tree is an undirected connected graph without cycles.

Let's consider a rooted undirected tree with n vertices, numbered 1 through n. There are many ways to represent such a tree. One way is to create an array with n integers p1, p2, ..., pn, where pi denotes a parent of vertex i (here, for convenience a root is considered its own parent).

For this rooted tree the array p is [2, 3, 3, 2].

Given a sequence p1, p2, ..., pn, one is able to restore a tree:

1. There must be exactly one index r that pr = r. A vertex r is a root of the tree.
2. For all other n - 1 vertices i, there is an edge between vertex i and vertex pi.

A sequence p1, p2, ..., pn is called valid if the described procedure generates some (any) rooted tree. For example, for n = 3 sequences(1,2,2), (2,3,1) and (2,1,3) are not valid.

You are given a sequence a1, a2, ..., an, not necessarily valid. Your task is to change the minimum number of elements, in order to get a valid sequence. Print the minimum number of changes and an example of a valid sequence after that number of changes. If there are many valid sequences achievable in the minimum number of changes, print any of them.

Input

The first line of the input contains an integer n (2 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n).

Output

In the first line print the minimum number of elements to change, in order to get a valid sequence.

In the second line, print any valid sequence possible to get from (a1, a2, ..., an) in the minimum number of changes. If there are many such sequences, any of them will be accepted.

Examples

input

4
2 3 3 4

output

1
2 3 4 4 

input

5
3 2 2 5 3

output

0
3 2 2 5 3 

input

8
2 3 5 4 1 6 6 7

output

2
2 3 7 8 1 6 6 7

Note

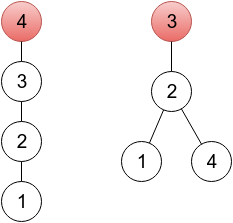
In the first sample, it's enough to change one element. In the provided output, a sequence represents a tree rooted in a vertex 4 (becausep4 = 4), which you can see on the left drawing below. One of other correct solutions would be a sequence 2 3 3 2, representing a tree rooted in vertex 3 (right drawing below). On both drawings, roots are painted red.

In the second sample, the given sequence is already valid.

题意：

给你n个顶点，n个数代表第i这个顶点连接的ai这个顶点，如果i=ai表示他没连向其他顶点，不过其他顶点可能连向他，然后问你至少改变多少个ai使得这n个顶点能变成一棵树

题解：

要最少的改变，我们分析一下，首先要成为一棵树，不能有孤立点，不能有环，所以我们只需要改变孤立点的连向和会使树变成环的点就行了，

我们这里用并查集维护连接的关系，任何孤立点都能当作树的顶点，如果有一个点会使其成为环，那么我们就暂时将这个点的当作这一棵树的顶点，

为什么是暂时呢？因为这一棵树有可能只是一棵小树，我们要合并全部的树，所以暂时当作这颗树的顶点，最后合并的时候就直接指向大树的顶点就行了，这样就能达到最小的改变，如果给的n个点形成的两棵子树，那么我们只需要任选一个树的顶点作为boss，然后改变另一棵树的顶点就能合并了。再总结一下，我们只改变了孤立点和会使其成为环的点然后合并子树的时候也只是改变了顶点的指向，这些都是必须要改变的，所以最后的答案肯定是最小的

#include<cstdio>
#define F(i,a,b) for(int i=a;i<=b;i++)
const int N=2E5+7;
int a[N],fa[N];

int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}

int main(){
    int n,boss=-1,cnt=0;
    scanf("%d",&n);
    F(i,1,n)fa[i]=i;
    F(i,1,n){
        scanf("%d",a+i);
        if(a[i]==i)boss=i,cnt++;//任意的孤立点或者任意一个集合的顶点都能当最终的顶点
        else{
            int fx=find(i),fy=find(a[i]);
            if(fx==fy){//说明这里存在环
                cnt++,a[i]=i;
            }else fa[fx]=fy;//将这两点连接
        }
    }
    if(boss==-1){
            F(i,1,n)if(fa[i]==i){boss=i;break;}
            cnt++;
    }
    printf("%d
",cnt-1);//因为多记了一个树的顶点
    F(i,1,n){
        if(a[i]==i)a[i]=boss;
        printf("%d%c",a[i]," 
"[i==n]);
    }
    return 0;
}