1.使用梯度下降来处理多元线性回归,下式使我们多元线性回归的假设式,这个模型的参数是从θ0到θn,这里我们不把它看做n个独立的参数,而是把这些参数看做一个n+1维的θ向量,我们的代价函数是J(θ0,θ1,θ2......θn)
但是这里我们不把J看做n+1个数的函数,我们使用更通用的方式将J谢春哥θ参数的向量函数,所以这里的θ是一个向量

(1)下面是梯度下降的式子,我们要不断的更新每个θj参数,

(2)接下来我们看看梯度下降函数。
当n=1的时候,即有1个特征的时候,按照梯度下降算法,我们有两个独立的更新规则,分别对应的是θ0和θ1,这一部分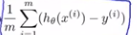 就是代价函数对参数θ0求偏导。同样的,我们还有一个不同的更新规则,针对的是参数θ1
就是代价函数对参数θ0求偏导。同样的,我们还有一个不同的更新规则,针对的是参数θ1

当我们有多个特征的时候(n>=1),我们就可以得到这个梯度下降的更新规则,
