MDP算法简介:首先MDP算法由五个单元组成(S、A、Psa(s')、R、G)

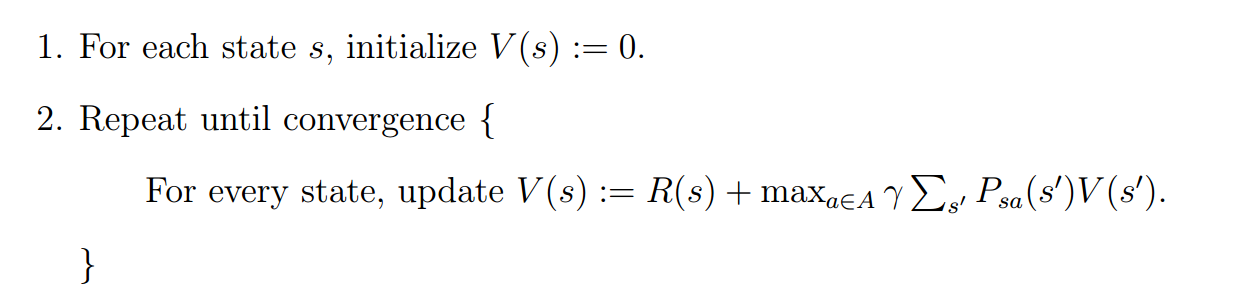
实现过策程的注意点:
如下图所示值函数
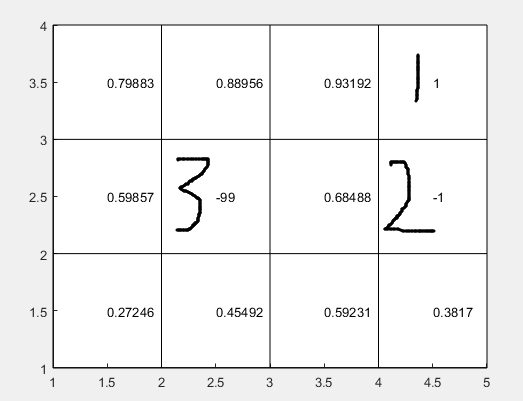
状态1为目标状态,状态2为避免状态,状态3为不存在状态
首先1状态和2状态的值在整个替代过程中不能改变,否则值函数不会收敛
其次3状态,不能使用非常低或者高的值函数参与运算,因为一旦参与运算会直接拉低其相邻状态的值函数
策略迭代法:
策略迭代方法发现有两个版本:
第一个版本是来源于:http://blog.csdn.net/zz_1215/article/details/44138843的版本

基本思路是:初始化策略与值函数
1、先按策略根据贝尔曼方程先让值函数收敛
2、然后按收敛的值函数求最佳策略
重复上述两个步骤直到策略不再变化
这个版本的策略迭代方法与值函数迭代方法关键的不同之处是在值迭代的时候,策略迭代方法是根据已有的固定策略进行值迭代的,而值函数迭代方法中的值迭代是局部最优策略的迭代
第二个版本是斯坦福大学机器学习公开课的版本:

该方法的2.(a)步骤的求解方法如下:

如文中所述是求解线性方程组而得的,首先方程组的构造的关键是根据贝尔曼方程构造出所有状态的表达式
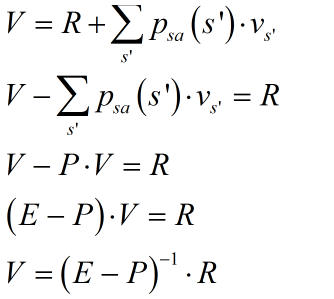
其中V、P、R、E分别为值函数矩阵、状态转移概率矩阵、回报函数矩阵、单位矩阵
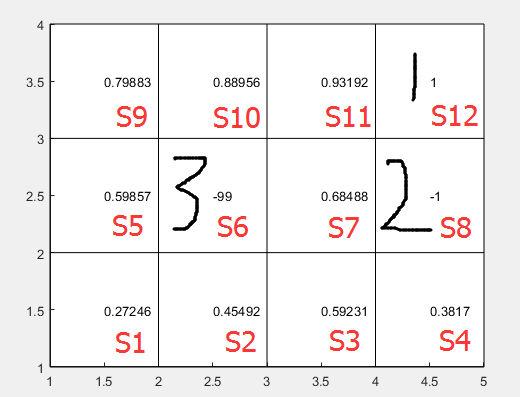
如上图所示的应用场景,总的状态数为12,对应的P为12×12的矩阵,由遍历所有状态(基于已有策略)的转移概率所得
其中需要注意的是:
1、S6是不参与运算的,所以要从矩阵呢运算中去除,所以去除V、P、E中的第六行与第六列所有元素以及R中的第六个元素
2、S8、S12的值函数是固定的所以V、P、E的第8行与第12行要从矩阵运算中去除,R的第八个与第12个元素去除
3、将下列条件
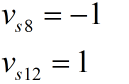
代入
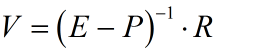
得
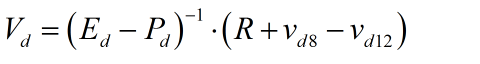
其中下d表示已经去除1、2中的行列之后的矩阵,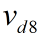 与
与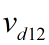 表示原V矩阵的第8列与第12列
表示原V矩阵的第8列与第12列
至此可求出所有状态的值函数
再进行策略迭代即可
这种方法的缺点是状态量非常大的时候求解方程组几乎是不可能的事情,因此只适合状态量不大的情况
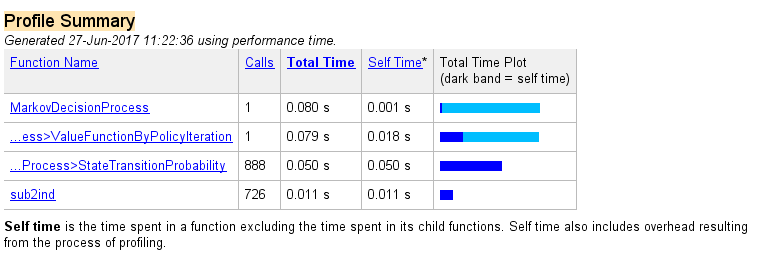
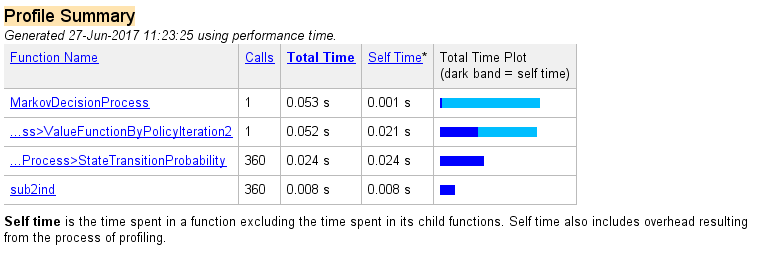
以下是三种方法执行情况对比:
值函数迭代方法:

策略迭代方法(版本一):
策略迭代方法(版本二):
在实现上述三种方法的过程中发现三种方法的收敛是不一样的
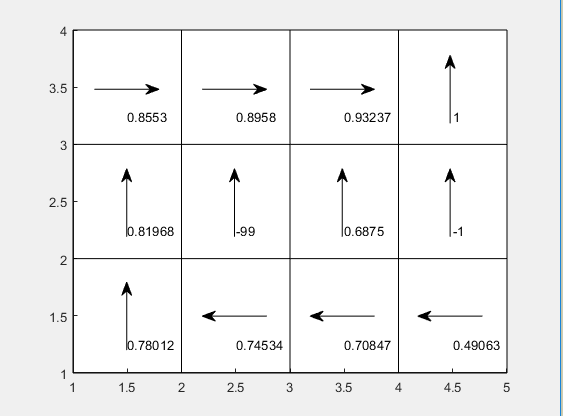
当转移概率的分布是0.8,0.1,0.1的分配方式时(即在S3状态采取向上的策略的话,状态转移的概率为:0.8概率转为S7,0.1概率转为S2,0.1概率转为S4)
收敛情况如下(小格子中的方向为策略方向,数值为值函数的值)
值函数迭代方法:
策略迭代方法(版本一):
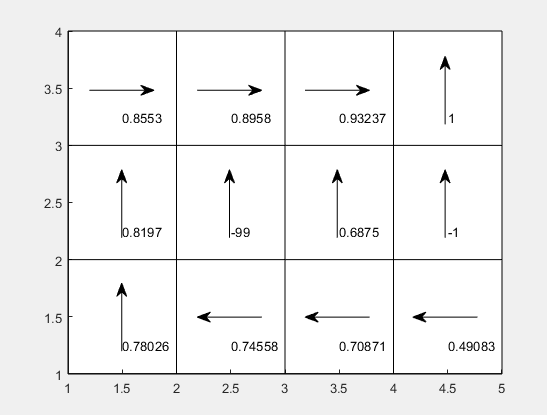
策略迭代方法(版本二):

发现策略迭代方法(版本二)的收敛结果与其他两个版本是不一样的
当转移概率的分布为:0.7,0.15,0.15时
收敛情况如下:
值迭代方法:

策略迭代法(第一版):
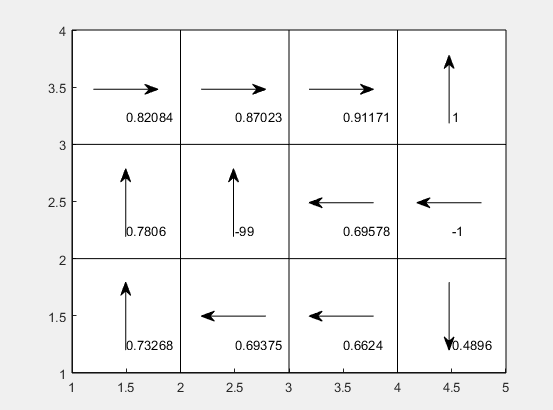
策略迭代法(第二版本):

发现策略迭代方法(版本二)的收敛结果与其他两个版本是不一样的
当转移概率的分布为:0.9,0.05,0.05时
收敛情况如下:
值函数迭代方法:

策略迭代方法(版本一):
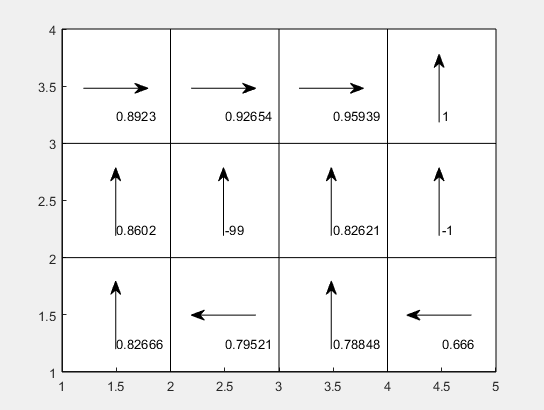
策略迭代方法(版本二):
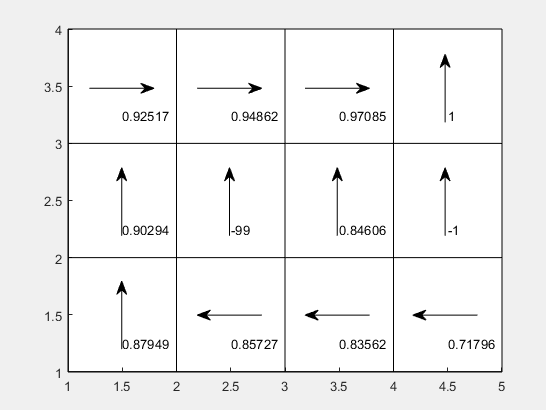
理论上来说,版本二的策略迭代方法是最接近贝尔曼方程思想的,但并没有收敛到最好的情况,本人还是菜鸟一只,并不是很理解为什么会这样,有朋友了解的,欢迎评论