这几天去搞了搞基础的算法,就把网络流放了几天,现在上来总结一下网络流的各种变体,有类似题目的话我尽量会附加。
最小割
所谓图的割,指的是对于某个顶点集合S, 从S发出指向S外部的那些边的集合,记为割(S, VS)。这些边的容量之和被称为割的容量。对应到流的图中,如果有源点s belong to S,, 而汇点t belong to (V S),那么此时的割又称为s - t割。如果将网络中s - t割的所有边都删除,也就不会再有s到t的路径。
最小割问题:对于给定网络,为了保证从s 到t没有路径,需要删除的边的总容量的最小值是多少?
最大流最小割定理:最大流的流量等于最小割的容量。
最大流的各种变体
1.多个源点的多个汇点的网络流:
建立超级源点s,并且建立从超级源点到其它源点的容量为无穷,建立超级汇点,从其它汇点到超级汇点建立一条容量为无穷的边。求出从s到t的最大流即可。
2.无向图上的最大流:
把无向图转换为有向图,只需要把无向图中容量为c的边建立一条反向边,两条边同时存在,求出最大流即可。
3.顶点上也有容量限制的情况:
图中不光边上有容量限制,途中经过的顶点也有总流入两个总流出量限制的情况应该如何处理呢?此时我们可以把每个顶点拆成两个顶点,拆点之后得到两个顶点分别为入顶点和出顶点,将指向原先顶点的边改成指向入顶点,将从原先顶点指出的边改成从出顶点指出。并且,再从入顶点向出顶点连容量为原先顶点容量的边,就可以把顶点上的容量限制转为边上的容量限制。
4.有最小流限制的情况:
是指每条边不光有最大流C限制,还有最小流量B的限制的情况,也即(B(e) <= f(e) <= C(e))。令f'(e) = f(e) - B(e),这就可以转化为只有最大流量限制的情况,也即0 <= f'(e) <= C(e) - B(e)。
而此时顶点对应的总流入量和总流出量的关系变为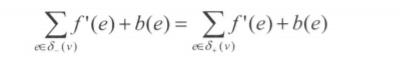
挖个坑,打完比赛再补上,现在要去做模版题了,嘤嘤嘤