最近来一波基础算法吧,掌握基础原理方可行走天下。回溯法本质是用来搜索问题的解,典型地就是使用深度优先搜索,搜索路径一般沿树形结构进行,在搜索过程中,首先会判断所搜索的树结点是否包含问题的解,如果肯定不包含,则不再搜索以该结点为根的树结点,而向其祖先结点回溯;否则进入该子树,继续按深度优先策略搜索。
可能这么说不是很容易懂,咱们来的实例吧,那就是经典的0-1背包问题,关于这一问题后边很多算法都会涉及到,咱们一点点深入~
我们还是使用典型的三背包为例,问题描述如下:设有三个背包,其重量分别为:16,15, 15;价值分别为: 45,25,25;请选择背包,使其重量不超过30,但价值最大。
可以看出我们的约束条件为总重量不超过30,目标是价值最大,那我们就可以使用回溯法的思想来求解:
每个背包都可以被选择中或者不选,理论上如果不加任何限制的话一共有八种可能(2×2×2),但我们在搜索的过程中要时刻注意总重量不可超过30 ,在这个基础上使其总价值最大,于是我们可以从第一个背包开始,先选中它,其重量是16,小于30,没有问题,然后在选择第二个背包,其重量为15,二者总重量为31,超过30,所以不能选择第二个背包,同理第三个背包也不能选,也就是说在选中第一个背包的前提下,另外两个背包就都不能再选了,这是八种理论可能情况中的一种;以此类推,不选第一个背包,在此基础上选择第二个背包,总重量为15,没有问题,再选第三个,此时总重量为30,也没有问题;对照这两种情况,前者总价值为45,后者总价值为50,当然,我们以上帝视角可以看出最大价值也就是50,但落实到具体的算法该如何全方位多角度深层次地解决这一问题呢?
我们来看一个完全二叉树结构图:
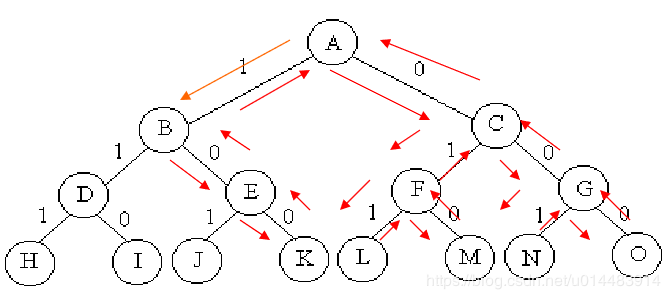
对于上述的背包问题,在此二叉树结构中可以简单地理解为:从A出发,往左子树方向走说明选中了A,往右子树方向走说明没有选中A,即“左选右不选”,落实到上图中就是1代表选中0代表未选中;我们上边说道的第一种情况,即只选中第一个背包的情况对应上图的A->B->E->K;那这里有朋友可能会问了为啥二叉树会有四层,不是一共三个背包嘛,对的,因为我们每一层所代表的背包选与不选都得由下一层所决定,比如节点E代表第三个背包,如果我们走到K就说明不选E,反之,若走到J则说明选中了E,因此三个背包我们需要四层完全二叉树,同理,若有N个背包则需要N+1层。
当我们的搜索路径到达K后,得到了一组值,即总重量为16,总价值为45,此时,由于已经到了树的叶子结点,因此需要回溯直到根,再继续进行后续的搜索,在后续搜索过程中,一方面要进行结点的判断,另一方面,一旦得到了一个合符要求的价值,则与前一次搜索所得到的结果进行比较,如果比前一次搜索得到的值大,则取代,反之,继续搜索直到整个树搜索结束所得到的最大值即为问题的解。
总的来说,上述的求解过程在程序实现过程中可以这样来理解:我们把二叉树的每一层看成是某一个物品。当我们选择物品时总是从第一个物品开始进行选择,可能选,也可能不选。如果选中,则从二叉树的左边子树开始搜索,如果未选中,则从二叉树的右边子树开始搜索。以此类推即可~
如果将每个物品的重量对应每一层的一个节点,在每次选择每一个物品时进行重量的判断,并记录权值,则可决定是否应该继续搜索下一层的子树。
如果设物品的重量存放在W数组中, W[i]为第i个物品的重量,P[i]表示第i个物品的价值。C表示背包能够承受的最大重量。cw表示当前物品的重量,cp表示当前物品的价值(稍微记忆一下这几个符号量的意义)。在选中情况下(即搜索左子树)执行下面的操作:
( 1 )首先判断加上该物品重量后是否满足最大重量不超过C的要求,如果不超过,则: cw+=w[i]; cp+=p[i]; 反之则搜索右子树;
( 2 )继续搜索下一层,执行相同的操作;
( 3 )当搜索到最后一层时,显然可得到从根到该结点所选择的所有物品的价值,如果该价值大于前一次得到的最大价值,则替代前一次的价值,反之,则不取代;
( 4 ) 退回到上一层,即其双亲结点所在的一层,显然此时应执行: cw-=w[i]; cp-=p[i];
执行上述语句的目的在于为访问右子树做准备。在访问右子树时,显然不需要计算其重量和价值,因为右子树表示未选中该物品
最后这几步是我在一些资料中看到的...总感觉有问题,尝试做了一些修改,还是有些别扭,其实大家也可以理解,算法这东西变幻莫测,再基本的原理也可以有很多表现形式,可以进一步优化,我们不要以上帝视角看待这个过程,这样会想当然地人为进行条件约束;
后续算法会继续优化,共同进步吧~~~~~~~~
本篇博文主要以文字为主,可能看起来很迷,但对于算法大家一定要沉下心来去思考,这样才能理解其原理,在此基础上更进一步,优化算法,使其更加完美^^
欢迎关注我的CSDN博客:https://blog.csdn.net/beyond9305