2.4.1 构造kd树
给定一个二维空间数据集,T={(2,3),(5,4),(9,6)(4,7),(8,1),(7,2)} ,构造的kd树见下图
2.4.2 kd树最近邻搜索算法
三、实现算法
下面算法实现并没有从构建kd树再搜索kd树开始,首先数据分为两部分,train数据和predict的数据,将train的数据抽取k个作为predict的最临近k节点,计算这k个数据和predict的距离,继续计算train中其他数据和predict的欧式距离,若小于k中欧式距离,那么替换较大的原始最临近k个节点中的数据,直到所有数据循环一遍为止,此时最临近k个节点就是predict数据在train中最临近节点,然后找出这k个节点出现次数最多的标签作为predict的标签。
还有一篇博文介绍knn非常详细
# coding=utf-8
import numpy as np
import pandas as pd
import time
def Predict(testset, trainset, train_labels):
predict = []
count = 0
for test_vec in testset:
# 输出当前运行的测试用例坐标,用于测试
print count
count += 1
knn_list = [] # 当前k个最近邻居
max_index = -1 # 当前k个最近邻居中距离最远点的坐标
max_dist = 0 # 当前k个最近邻居中距离最远点的距离
# 先将前k个点放入k个最近邻居中,填充满knn_list
for i in range(k):
label = train_labels[i]
train_vec = trainset[i]
dist = np.linalg.norm(train_vec - test_vec) # 计算两个点的欧氏距离
knn_list.append((dist, label))
# 剩下的点
for i in range(k, len(train_labels)):
label = train_labels[i]
train_vec = trainset[i]
dist = np.linalg.norm(train_vec - test_vec) # 计算两个点的欧氏距离
# 寻找10个邻近点钟距离最远的点,///应该有一个函数代替循环吧
if max_index < 0:
for j in range(k):
if max_dist < knn_list[j][0]:
max_index = j
max_dist = knn_list[max_index][0]
# 如果当前k个最近邻居中存在点距离比当前点距离远,则替换
if dist < max_dist:
knn_list[max_index] = (dist, label)
max_index = -1
max_dist = 0
# 统计选票
class_total = 10
class_count = [0 for i in range(class_total)]
for dist, label in knn_list:
class_count[label] += 1
# 找出最大选票
mmax = max(class_count)
# 找出最大选票标签
for i in range(class_total):
if mmax == class_count[i]:
predict.append(i)
break
return np.array(predict)
k = 10
if __name__ == '__main__':
time_1 = time.time()
raw_data = pd.read_csv('D:\Python27\yy\data\Digit Recognizer\train.csv')
raw_test = pd.read_csv('D:\Python27\yy\data\Digit Recognizer\test.csv')
test_features = raw_test.values
data = raw_data.values
train_features = data[0::, 1::]
train_labels = data[::, 0]
time_2 = time.time()
print 'read data cost ', time_2 - time_1, ' second', '
'
print 'Start predicting'
test_predict = Predict(test_features, train_features, train_labels)
time_3 = time.time()
print 'predicting cost ', time_3 - time_2, ' second', '
'
一、K近邻算法
k近邻法(k-nearest neighbor,k-NN)是一种基本分类与回归方法,输入实例的特征向量,输出实例的类别,其中类别可取多类
k近邻法只是利用训练数据集对特征向量空间进行划分,所以选取的训练数据一定要保证样本分布均匀。
算法思路:给定一个训练数据集,对于新输入实例,在训练数据集中找到与该实例最临近的k个实例

二、k近邻模型
2.1 距离度量
特征空间中两个实例点的距离就是两个实例点相似程度的反应
距离定义: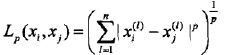
(1)当p=1,称为曼哈顿距离
(2)当p=2,称为欧式距离
(3)当p取无穷大时,它是各个坐标距离的最大值 max|xi-xj|
注意:p值的选择会影响分类结果,例如二维空间的三个点 x1=(1,1),x2=(5,1), x3=(4,4)
由于x1和x2只有第二维上不同,不管p值如何变化,Lp始终等于4,而L1(x1,x3)=3+3=6,L2(x1,x3)=(9+9)1/2=4.24,L3(x1,x3)=(27+37)1/3=3.78,L4=3.57……
当p=1或2时,X2和X1是近邻点
2.2 k值的选择
在应用中,k值一般取一个较小的数值,通常采用交叉验证法来选取最优k值
k较小时,模型复杂,容易过拟合
k较大时,模型简单
2.3 分类决策规则
使用多数表决规则,即少数服从多数
