Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]
class Solution:
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices)<=1:
return 0
s0 = [-prices[0]]
s1 = [0]
s2 = [0]
for i in range(1,len(prices)):
s0.append(max(s0[i-1],s2[i-1]-prices[i]))
s1.append(s0[i-1]+prices[i])
s2.append(max(s1[i-1],s2[i-1]))
return max(s2[-1],s1[-1])
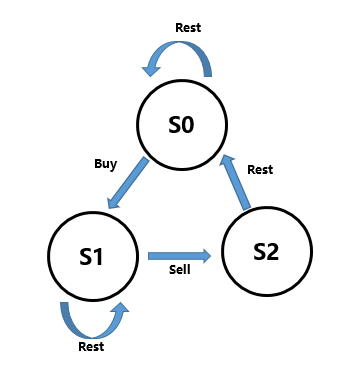
用一个三个状态的有限自动机来表示。
则
- s0[i] = max(s0[i-1], s2[i-1])
- s1[i] = max(s1[i-1], s0[i-1] - price[i])
- s2[i] = s1[i-1] + price[i]
因为在sell之后一定要休息,所以需要三个状态
参考自:https://www.cnblogs.com/jdneo/p/5228004.html