人生第一道计算几何题? 留作纪念(QAQ)
凸包是什么?下图就是一个土包

我们怎么求出凸包呢
我们先把凸包分成上下两个部分
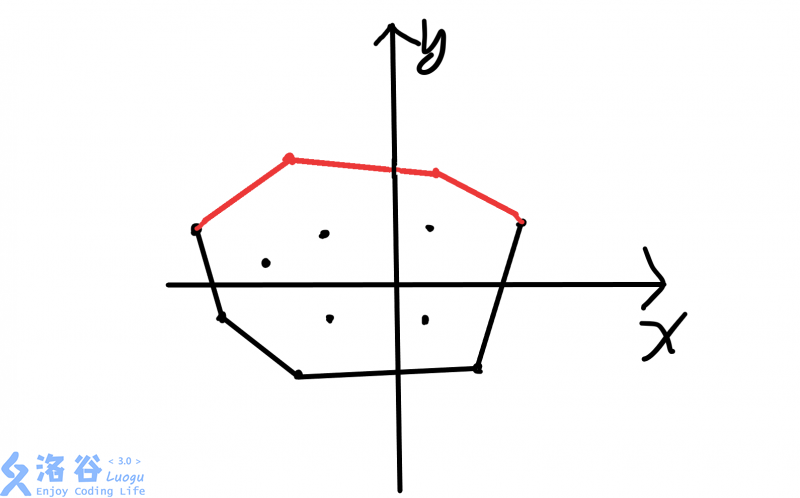
如图,红色部分称为上半部分,黑色部分成为下半部分
然后按照x为第一关键字,y为第二关键字排序
于是第一个就会找到最左边的一个最下面的点,第二个就会找到最右边的一个最上面的点
我们以这两个点为分界线,分出上下两个凸包分别求出周长
我们维护一个栈,栈中的元素即为上(下)凸包所有元素
对于下半部分,我们显然要让斜率尽可能地小
我们先把前两个点(分别为AB)入栈,拓展到第三个点(C),若(K_{AC}<K_{AB})则把C进栈,否则将B弹出并将C进栈,不断弹出直到(K_{AC}>K_{AB})
而对于上半部分,我们是要让斜率尽可能大
同理,我们先把后两个点(分别为FE)入栈,拓展到第三个点(D),若(K_{FD}<K_{ED})则把D进栈,否则将E弹出并将D进栈,不断弹出直到(K_{FD}>K_{ED})
于是我们就可以得到上下两个凸包的所有点,再用距离公式算就可以了,时间复杂度(O(N))
代码如下:
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define re register
#define D double
#define inf 123456789
il int read()
{
re int x = 0, f = 1; re char c = getchar();
while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') x = x * 10 + c - 48, c = getchar();
return x * f;
}
#define rep(i, s, t) for(re int i = s; i <= t; ++ i)
#define drep(i, s, t) for(re int i = t; i >= s; -- i)
#define Next(i, u) for(re int i = head[u]; i; i = e[i].next)
#define mem(k, p) memset(k, p, sizeof(k))
#define maxn 10005
struct node{D x, y;}e[maxn];
int n, st[maxn], top;
D ans;
//il D ff(int x){return x * x;}
#define ff(x) (x) * (x)
il bool cmp(node a, node b){return a.x == b.x ? a.y < b.y : a.x < b.x;}
il D dis(int x, int y){return sqrt(ff(e[x].x - e[y].x) + ff(e[x].y - e[y].y));}
il D getk(int x, int y){return e[x].x == e[y].x ? inf : (e[x].y - e[y].y) / (e[x].x - e[y].x);}//注意这里一定要判断两个x相等的情况
int main()
{
n = read();
rep(i, 1, n) scanf("%lf%lf", &e[i].x, &e[i].y);
sort(e + 1, e + n + 1, cmp);
rep(i, 1, n)
{
st[++ top] = i;
while(top > 2 && getk(st[top], st[top - 2]) < getk(st[top - 1], st[top - 2]))
st[top - 1] = st[top], -- top;
}
rep(i, 1, top - 1) ans += dis(st[i], st[i + 1]);
top = 0;
drep(i, 1, n)
{
st[++ top] = i;
while(top > 2 && getk(st[top], st[top - 2]) < getk(st[top - 1], st[top - 2]))
st[top - 1] = st[top], -- top;
}
rep(i, 1, top - 1) ans += dis(st[i], st[i + 1]);
printf("%.2lf", ans);
return 0;
}