Mayor's posters
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 29495 | Accepted: 8531 |
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers li and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= li <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered li, li+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.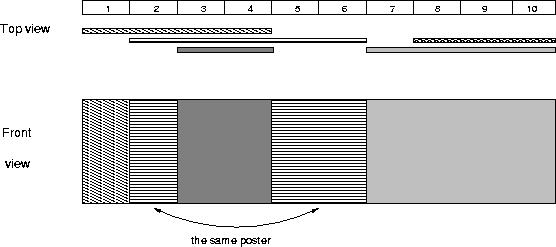
The picture below illustrates the case of the sample input.

Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
Source
分析:线段树:成段替换,查询所有出现的数据种类。PS:离散化预处理,注意点和边的区别
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 int col[1 << 17]; int ans; typedef struct S { int pos, id; } NODE; NODE node[20010]; bool cmp(NODE a, NODE b) { return a.pos < b.pos; } int ls[20010]; int vis[40010]; void pushdown(int rt, int len) { if (col[rt] != -1) { col[rt << 1] = col[rt << 1 | 1] = col[rt]; col[rt] = -1; } } void update(int L, int R, int c, int l, int r, int rt) { if (L <= l && R >= r) { col[rt] = c; return; } pushdown(rt, r - l + 1); int m = (l + r) >> 1; if (L <= m) update(L, R, c, lson); if (R > m) update(L, R, c, rson); } void query(int l, int r, int rt) { if (col[rt] != -1) { if (!vis[col[rt]]) { vis[col[rt]] = 1; ++ans; } return; } if (l == r) return; int m = (l + r) >> 1; query(lson); query(rson); } int main() { int T, i, j, n, max; scanf("%d", &T); while (T--) { scanf("%d", &n); memset(col, -1, sizeof (col)); memset(vis,0,sizeof(vis)); for (i = 0; i < n; ++i) { node[i << 1].id = i << 1; scanf("%d", &node[i << 1].pos); node[i << 1 | 1].id = i << 1 | 1; scanf("%d", &node[i << 1 | 1].pos); } sort(node, node + n + n, cmp); ls[node[0].id] = 0; for (i = 1; i < n + n; ++i) { if (node[i].pos == node[i - 1].pos) { ls[node[i].id] = ls[node[i - 1].id]; } else if (node[i].pos == node[i - 1].pos + 1) { ls[node[i].id] = ls[node[i - 1].id] + 1; } else { ls[node[i].id] = ls[node[i - 1].id] + 2; } } max = ls[node[n + n - 1].id]; for (i = 0; i < n; ++i) { update(ls[i << 1], ls[i << 1 | 1], i, 0, max, 1); } ans = 0; query(0, max, 1); printf("%d\n", ans); } return 0; }