参考资料:
算法进阶课(试听课)——网络流的基本概念_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
《数学建模算法与应用》司守奎第二版
《ASM/ICPC算法训练教程》余立功 主编
一,网络流问题的概念
1,网络与流
给一个有向图 D=(V, A),其中 A 为弧集,在 V 中指定一点,称为源点(或发点),记为 s,另一点称为汇点(或收点),记为 t,其余的点叫中间点。对于每一条弧(vi, vj) 属于 A,对应有一个 cij >= 0,称为弧的容量。通常把这样的有向图 D 叫做一个网络,记为 D = (V, A, C),其中 C ={ cij }。
网络上的流,是指定义在弧集合 A 上的一个函数 f = { fij },我们将 fij 称为弧(vi, vj) 上的流量。
2,可行流
网络流就是可行流。可行流总是存在的,比如至少有一个零流。满足下列条件的流 f 称为可行流:
(1)容量限制:0 <= fij <= cji
(2)反对称性:fij = -fji
(3)流量平衡:对于中间点,流入该节点的流量和等于流出该节点的流量和。
结合(2)(3),对于中间点v有:Σ(u<=V) f(v, u) = 0;对于源点和汇点有:Σ(u<=V) f(s, u) = -Σ(u<=V) f(t, u)
3,最大流
定义一个网络的流量:源点的净输出量。
最大流问题就是在所有可行流中,源点的净输出量大的那个可行流
4,增广路
给定一个可行流 f = fij,把网络中 fij = cij 的弧称为饱和弧,fij < cij 的弧称为非饱和弧。把 fij = 0 的弧称为零流弧,把 fij > 0 的弧称为非零流弧。
若 P 是网络中连接源点和汇点的一条路,定义流的方向s->t,则路上的弧被分为两类:一类与流的方向一致,称为前向弧;另一类与流的方向相反,称为后向弧(反向边)。
增广路定义①:给定一个可行流 f,若 P 是网络中连接源点和汇点的一条路,若 P 满足:前向弧是非饱和弧,后向弧是非零弧,则称 P 为关于 f 的一条增广路。
增广路定义②:在一个可行流对应的残余网络中,从源点出发,沿着容量 > 0 的弧,到达汇点的路径。
5,残余网络
Gf 表示残余网络,Ef 表示残余网络的边集,rij 为残余网络的容量。给定一个可行流 f1 (注意:一个可行流对应一个残余网络),其中
Ef1 = f1 的边集 + f1 的边集的反向边
rij = cij -fij (当弧 ij 为前向弧时)
= fij (当弧 ij 为反向边时)
如果网络中一条边的容量为 0,则认为这条边不在残余网络中。
6,反向边的作用
修改当前的可行流,因为原先尝试的可行流可能是错误的,而反向边可以给你将流进来的退回去的机会,即取消先前的错误行为。
比如说我们得到下图的可行流:
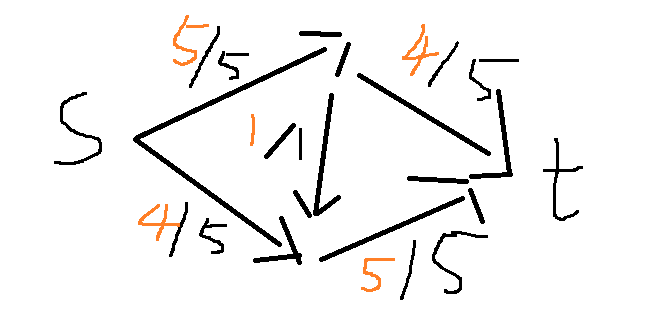
可以注意到该可行流并不是最大流,但是不加上反向边的话,却又难以发现,这个才是最大流:
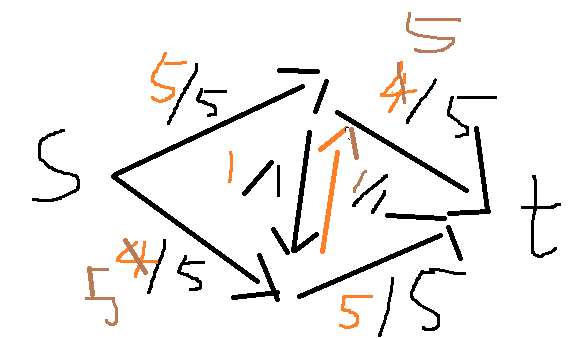 即:
即: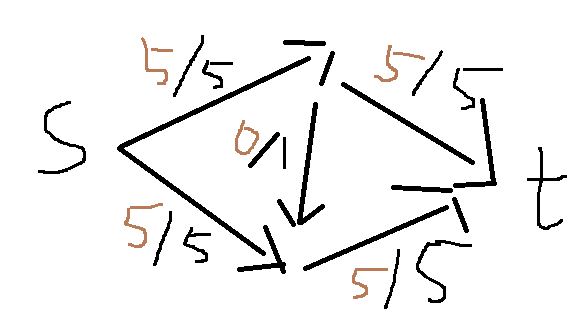
7,定理
① 设一可行流 f,和它对应的残余网络Gf 的一个可行流 f',则:
f + f' 也是原网络的可行流,且 | f + f' | = | f | + | f' | (根据残余网络的概念推导)
证明:两个流相加,就是对应边的流量相加
① 容量限制:当 f 和 f' 中的边同向时:f‘ij <= cij - fij,所以 f'ij + f'ij <= cij,所以 f + f' 满足容量限制。
当 f 和 f' 中的边同向时:f‘ij <= fji <= cji,所以 0 <= fji - fij <= cij,所以 f + f' 满足容量限制。
② 流量平衡:两个等式相加等式仍然成立,所以流量也是平衡的。
② 然后由:| f + f' | = | f | + | f' | 。我们可以推出:
如果残余网络存在流量 > 0 的可行流,则原网络的可行流必然不是最大流。
③ 那么反之:
如果原网络的可行流 f 对应的残余网络的所有可行流皆为零流,则 f 为最大流。(反之不一定成立,但该反之成立,要用到割来证明)
8,流网络的割
割:设流网络 G = (V, E),割就是对点集 E 划分:它将 E 分成两个子集:S,T,其中 S 并 T = V,S 交 T = 空集,s 属于 S,t 属于 T。一个有 n 个顶点的网络,有 2n-2 种割的方法。
割的容量:所有从 S 指向 T 的边的容量之和。记为 c(S, T)
最小割: 2n-2 种割的方法中,容量最小的割。
割的流量:给定一个可行流,从 S 流向 T 的流量和 - 从 T 流向 S 的流量和。记为 f(S,T)
性质①:对于流网络的任意一个割和任意一个可行流,f(S,T) <= c(S,T)
证明:从 S 流向 T 的流量和 <= c(S, T),所以 从 S 流向 T 的流量和 - 从 T 流向 S 的流量和 <= c(S, T)
性质②:f(S,T) = | f |
证明:https://www.bilibili.com/video/BV1VV411r73E?from=search&seid=10016382068478400791 64:00
由①②可得:| f | <= c(S,T),所以 最大流 <= 最小割的流量 (最大流最小割定理)
9,最大流最小割定理
对于一个流网络 G = (V,E),和它的任意一个可行流 f。有以下三点相互等价。
① f 是最大流
② Gf 中不存在增广路径
③ 存在一个割 【S,T】,| f | = c(S, T)
证明:
① -> ②:反证法:若 f 是最大流,且 Gf 存在增广路径 f',则有:| f + f' | = | f | + | f' | > | f |,与 f 是最大流相互矛盾,得证。
③ -> ①:因为:| f | <= c(S,T),且 | f | = c(S, T)。所以 | f | 是最大流。
② -> ③:
第一步:构造一个割【S,T】,其中S:在 Gf 中从源点出发沿着容量 > 0 的边所能走到的点集(因为Gf 中不存在增广路径,所以必然走不到汇点);T = V - S。
第二步:对于 S 中一点 x,T 中一点 y,有:f(x, y) = c(x, y),(反证法:因为若 f(x, y) < c(x, y),则残余网络中必然有 x->y 的边且容量 > 0,则 y 必然在 S 中,矛盾,得证)。
第三步:同理可证:f(y, x) = 0
第四步: 因为从集合 T 到集合 S 的流量和为 0,所以 c(S, T) = f(S, T)
第五步:因为 | f | = f(S,T),且 c(S, T) = f(S, T),所以 | f | = c(S, T)
得证。
因为有①->②->③->①,所以,任意两点等价。
这里我们要用到的是:如果Gf中不存在增广路径,则Gf对应的f是最大流。而要证明这点,却要通过②->③->①来证明。
二,算法
1,EK( Edmonds-Karp ) 算法
实质:迭代维护残余网络
while()
① 找增广路径(BFS)
② 更新残余网络:
· rij = cij -fij (当弧 ij 为前向弧时)
= fij (当弧 ij 为反向边时)
其中 fij 为该增广路径上 最大但又满足容量限制的流量。
时间复杂度 O(n*m*m):虽然大,但执行效率高,可以处理 10000~100000 点的网络。
注意点①:增广路径不可以看成是一个可行流,因为它的流量并不能保证所有的边满足容量限制。但同 f + f' 也是原网络的可行流 的证明一样,f + 有流量的增广路径 也是原网络的可行流。注意:这里的增广路径流量取值可以为:0~增广路径上的最小容量值,代码中增广路径流量取增广路径上的最小容量值,这样可以减少找增广路径的次数。
注意点②:存残余网络的方法:不能用邻接矩阵,因为有重边和自环。所以用链式前向星,用连续的两个位置存两个点的前向弧和反向边,比如 0 存第一条边的前向弧,1 存第一条边的反向边;2 存第一条边的前向弧,3 存第一条边的反向边。这样就可以通过异或 1得到相反的边。如:0^1=1,1^1=0,2^1=3,3^1=2。
注意点③:找增广路径是在残余网络中找的,而最大流是通过将所有增广路径加起来得到的。在代码中,残余网络用数组 r 表示,增广路径的流量用 f 表示。
所以,初始时,原网络的最大流为 0,其对应的残余网络的前向边为 cij,反向边为 0。体现在代码中为:
add(u, v, w); // 前向弧 add(v, u, 0); // 反向边
每找到一条增广路径后,最大流都要加上增广路径的流量,残余网络也要根据最大流的变化做出对应的更改,注意反向边根据容量限制要加上增广路径的流量。体现在代码中就是
maxf += f[t]; // 当前增广路径的流量
for (int i = t; i != s; i = to[p[i] ^ 1])
{
r[p[i]] -= f[t]; // 前向弧
r[p[i] ^ 1] += f[t]; // 反向边
}
注意点④:在代码中求增广路径上的最小容量值是用 f数组 的,为什么要用数组而不是一个 int 呢? 因为BFS在遍历时可能会遍历到其他边,你如果只用一个 f变量,就有可能求到的最小容量的那条边不是增广路径上的边。所以需要用 f数组 记录每找到一个点后容量的最小值,便于回溯。而如果是在 EK函数中直接遍历求容量的最小值,一个 int f 足以!
注意点⑤:因为DFS会被卡数据,导致超时,具体怎么做的,我也不太清楚,所以一般都是用BFS遍历。
题目:https://www.acwing.com/problem/content/description/2173/
代码:

#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> #include<string.h> #define N 1010 #define M 20010 #define inf (int)1e8 int n, m, s, t; // 顶点数 边数 起点 终点 int last[N], pre[M], to[M], tot = 0, r[M]; // 链式前向星, r[i]:残余网络中第 i 条边的容量 int f[N]; // 记录当前增广路径上,到点 i 为止所有边的最小容量,所以当i==t 时,即代表增广路径的最小容量,即代表增广路径的流量 int p[N]; // 记录增广路径上,该点的前驱边的编号 int q[N]; // 队列 bool vis[N]; // 遍历时标记是否搜索过 void add(int u, int v, int w) // 加边函数 { to[tot] = v; r[tot] = w; pre[tot] = last[u]; last[u] = tot++; } bool bfs() // BFS 找增广路 { int first = 0, rear = 0; memset(vis, false, sizeof(vis)); q[0] = s; vis[s] = true, f[s] = inf; while (first <= rear) { int vertex = q[first++]; // 出队列 for (int i = last[vertex]; ~i; i = pre[i]) { int next = to[i]; // 该起点对应的终点 if (!vis[next] && r[i]) // 如果该点还没有遍历过且容量 > 0 { vis[next] = true; f[next] = f[vertex] < r[i] ? f[vertex] : r[i]; // 记录当前路径上所有边的最小容量 p[next] = i; if (next == t) // 遍历到终点结束 return true; q[++rear] = next; // 入队列m } } } return false; // 无法遍历到终点,表示没有增广路径了 } int EK() { int maxf = 0; while (bfs()) { maxf += f[t]; // 当前增广路径的流量 // to[p[i] ^ 1] 不用管 p[i] 是前向弧还是反向边,只是求反过来的那条边的终点,即该边的起点 for (int i = t; i != s; i = to[p[i] ^ 1]) { r[p[i]] -= f[t]; // 前向弧 r[p[i] ^ 1] += f[t]; // 反向边 } } return maxf; } int main(void) { scanf("%d%d%d%d", &n, &m, &s, &t); memset(last, -1, sizeof(last)); while (m--) { int u, v, w; // 顶点及容量 scanf("%d%d%d", &u, &v, &w); add(u, v, w); // 前向弧 add(v, u, 0); // 反向边 } printf("%d ", EK()); system("pause"); return 0; }
=========== ========= ======= ====== ===== ==== === == =
闻乐天授江州司马 元稹 〔唐代〕
残灯无焰影幢幢,此夕闻君谪九江。
垂死病中惊坐起,暗风吹雨入寒窗。
