可持久化线段(主席树)详解(两个题目):
本篇博客借鉴了此篇博客,补充了一些自己的理解
现有这样一个题目:
给定长为n的一个序列,q次询问,每次询问l,r区间内第k大的数是多少
(n,q<=200,000)
求解这个问题,我们便要用到主席树。
首先了解一下什么叫主席树:
主席树,即可持久化线段树,是支持查询历史版本的一种线段树的升级版
主席树是,对于一个序列[1...n]的每一个前缀[1...i]都建立一颗线段树。我们知道线段树的每一个节点对应的是一个区间[l, r],则每一个节点对应的sum[rt是在的[1...i]中的数,在区间[l, r]的有多少个。询问时利用前缀的思想进行求解的一种树。(不理解没关系我们慢慢讲)
下面我们详细讲一下怎么写主席树:
先做好准备工作,因为主席树一个区间[l , r]代表的是[l , r]的数,所以我们要把数据离散化,才能用主席树表示。
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
}
之后便是主席树的部分了。
我们用一组数据来讲一下:
3 1
3 1 2
1 2 2
- 首先建一棵空树,建树中不同于线段树的有几点:
- 主席树因为在建立n棵树的时候必须要利用当前树和前一棵树的相似之处,所以左右节点和根节点之间可能不满足lson = rt << 1, rson = rt << 1 | 1。所以我们在建树时直接用一个计数器++来记录当前节点是哪个节点。
- 在建树时,用L数组和R数组记录这个节点指向左右子树的根节点的值。
int build(int l, int r) {//建一棵空树
int rt = ++cnt;
sum[rt] = 0;
if (l < r) {
L[rt] = build(l, mid);
R[rt] = build(mid + 1, r);
}
return rt;
}
建完后如图:
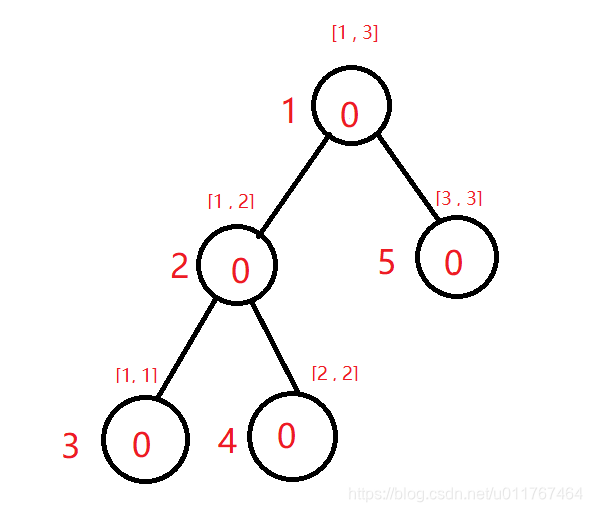
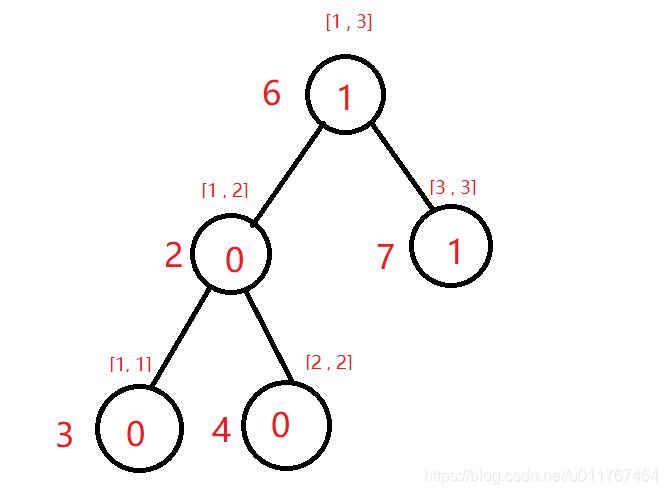
- 再建n棵前缀的树,我们先看图:
第一棵
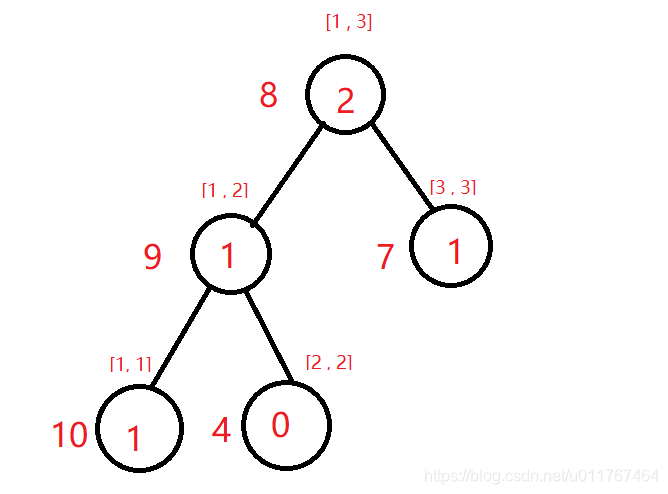
第二棵:
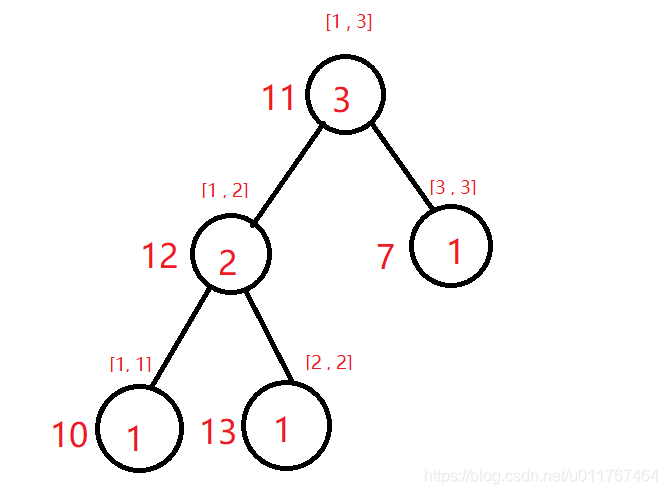
第三棵:
要注意的有几点:
- 如果对于每一棵[1...i]的树都建立一颗完整的线段树,那么空间复杂度必然爆炸。所以我们要利用第i棵线段树和第i - 1棵线段树的相同特征来建树,我们观察到第i棵树和第i - 1棵树之间仅有一条路径不同,对于这条路径建树的空间复杂度仅为log(n)级别,其他的部分我们只要复制上一棵树的就可以了,这样总复杂度为nlogn。
- 关于如何复制,我们之前有L和R数组,分别指向左右子树,我们在建一棵新树时,先让这棵新树的每一个结点的左右节点指向原来的树的左右节点,之后递归修改sum的时候,我们把新的路径的节点值返回给对应的L和R数组,这样就对于这条路径的每一个点都有一个正确的L, R,达到了建树的目的。
- 递归经过的地方必然会使这个节点对应的sum++。
- 之后便是询问:
我们现在有n棵线段树,每颗线段树都存了到i为止的所有区间的数的个数。我们可以很容易明白询问是满足可减性的,因为假设我要询问序列[2 , 5]内3的个数,就可以用[1 , 5]内3的个数减去[1 , 2]内3的个数。
对于[l , r]区间求第k大,我们每次可以算出第r棵线段树内和第l - 1棵线段树内左子树sum的差值x,这个差值x就说明了左子树对应的数的区间有多少个数,假如这个数大于等于k,我们就接着向左子树找,否则我们就向右子树找k - x。即可找到对应的第k大。
int query(int u, int v, int l, int r, int k) {
if (l >= r) return l;
int x = sum[L[v]] - sum[L[u]];
if (x >= k) return query(L[u], L[v], l, mid, k);
else return query(R[u], R[v], mid + 1, r, k - x);
}
题目地址:洛谷P3834
最后附上完整ac代码:
#include<bits/stdc++.h>
#define maxn 2000050
#define mid ((l + r) >> 1)
using namespace std;
int a[maxn], b[maxn], T[maxn];
inline int getnum() {
char c; int ans = 0; int flag = 1;
while (!isdigit(c = getchar()) && c != '-');
if (c == '-') flag = -1; else ans = c - '0';
while (isdigit(c = getchar())) ans = ans * 10 + c - '0';
return ans * flag;
}
int L[maxn << 5], R[maxn << 5];//指向左子树和右子树的根
int sum[maxn << 5];//离散化去重后的每个节点所包含的数的个数
int cnt;//所有节点的计数器
int build(int l, int r) {//建一棵空树
int rt = ++cnt;
sum[rt] = 0;
if (l < r) {
L[rt] = build(l, mid);
R[rt] = build(mid + 1, r);
}
return rt;
}
int update(int pre, int l, int r, int x) {
int rt = ++cnt;
L[rt] = L[pre], R[rt] = R[pre], sum[rt] = sum[pre] + 1;
if (l < r) {
if (x <= mid) L[rt] = update(L[pre], l, mid, x);
else R[rt] = update(R[pre], mid + 1, r, x);
}
return rt;
}
int query(int u, int v, int l, int r, int k) {
if (l >= r) return l;
int x = sum[L[v]] - sum[L[u]];
if (x >= k) return query(L[u], L[v], l, mid, k);
else return query(R[u], R[v], mid + 1, r, k - x);
}
int main() {
int n = getnum(), q = getnum();
for (int i = 1; i <= n; i++) {
a[i] = getnum();
b[i] = a[i];
}
sort(b + 1, b + n + 1);
int m = unique(b + 1, b + n + 1) - b - 1;
T[0] = build(1, m);
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
T[i] = update(T[i - 1], 1, m, a[i]);
}
while (q--) {
int x = getnum(), y = getnum(), z = getnum();
printf("%d
", b[query(T[x - 1], T[y], 1, m, z)]);
}
return 0;
}
我们再做一个主席树的题练练手:
CSU 1981: 小M的魔术表演
题面
Description
小M听说会变魔术的男生最能吸引女生注意啦~所以小M费了九牛二虎之力终于学会了一个魔术:
首先在桌面上放N张纸片,每张纸片上都写有一个数字。小M每次请女生给出一个数字x,然后划定任意一个区间[L,R],小M就能立马告诉对方这个区间内有多少个数字比x小。
小M当然是知道答案的啦,但是你呢?
Input
第一行为一个数字T(T<=10)表示数据组数
第二行为两个数字n、m(1<=n,m<=200000)表示序列长度和询问次数
第三行为n个数字表示原始序列A (0 < A[i] < 1000000000)
接下来m行,每行三个数字l r x 表示询问[l,r]之间小于x的有几个(1<=l<=r<=n,0<=x<=1000000000)
保证数据合法
Output
输出为m行,第i行表示第i个询问的答案
Sample Input
1
10 3
2 3 6 9 8 5 4 7 1 1
1 3 5
2 8 7
3 6 4
Sample Output
2
4
0
题解
这个题也是主席树,我们只需改动几个小地方即可
#include<bits/stdc++.h>
#define maxn 200050
#define mid ((l + r) >> 1)
using namespace std;
int a[maxn], b[maxn], T[maxn];
inline int getnum() {
char c; int ans = 0; int flag = 1;
while (!isdigit(c = getchar()) && c != '-');
if (c == '-') flag = -1; else ans = c - '0';
while (isdigit(c = getchar())) ans = ans * 10 + c - '0';
return ans * flag;
}
int L[maxn << 5], R[maxn << 5];//指向左子树和右子树的根
int sum[maxn << 5];//离散化去重后的每个节点所包含的数的个数
int cnt;//所有节点的计数器
int build(int l, int r) {//建一棵空树
int rt = ++cnt;
sum[rt] = 0;
if (l < r) {
L[rt] = build(l, mid);
R[rt] = build(mid + 1, r);
}
return rt;
}
int update(int pre, int l, int r, int x) {
int rt = ++cnt;
L[rt] = L[pre], R[rt] = R[pre], sum[rt] = sum[pre] + 1;
if (l < r) {
if (x <= mid) L[rt] = update(L[pre], l, mid, x);
else R[rt] = update(R[pre], mid + 1, r, x);
}
return rt;
}
int query(int u, int v, int l, int r, int k) {
if (l >= r) {
if (l != k)
return sum[v] - sum[u];//找到不等于k的才返回这个
else return 0;//因为题中让求小于k的,等于k的返回0
}
int ans = sum[L[v]] - sum[L[u]];//个数
if (mid >= k) return query(L[u], L[v], l, mid, k);//大于k,向左子树找
else return ans + query(R[u], R[v], mid + 1, r, k);//否则向右子树找,加上左子树的个数
}
int main() {
int t = getnum();
while (t--) {
int n = getnum(), q = getnum();
cnt = 0;
memset(L, 0, sizeof(L));
memset(R, 0, sizeof(R));
memset(sum, 0, sizeof(sum));
memset(T, 0, sizeof(T));
for (int i = 1; i <= n; i++) {
a[i] = getnum();
b[i] = a[i];
}
sort(b + 1, b + n + 1);
int m = unique(b + 1, b + n + 1) - b - 1;
T[0] = build(1, m);
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
T[i] = update(T[i - 1], 1, m, a[i]);
}
while (q--) {
int x = getnum(), y = getnum(), z = getnum();
z = lower_bound(b + 1, b + m + 1, z) - b;
printf("%d
", query(T[x - 1], T[y], 1, m, z));
}
}
return 0;
}