树状数组与线段树

引入

线段树和树状数组，是两个十分相似的数据结构。他们能使对一个区间的数修改以及查询的速度提升许多。两个结构本质相同，各有优缺点，今天我们来从单点修改，单点查询，区间修改，区间查询。

概念

线段树

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。

比如讲一个有4个数的线段树，是长这个样子的：

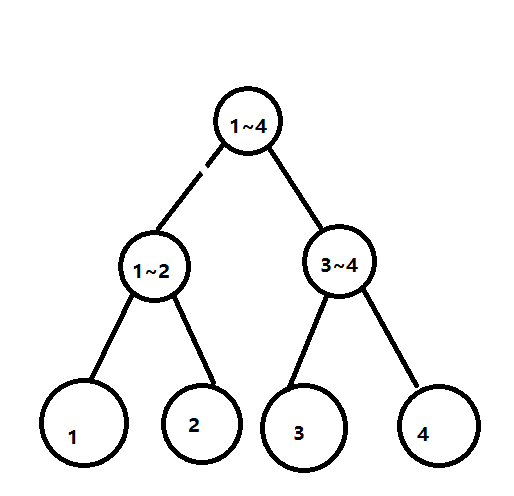
一号节点，代表着区间1~4

二号节点，代表区间1~2

三号节点，代表区间3~4

以此类推。。。。。。

很容易发现，对于n号节点来说，n×2代表着它的区间的前半段，n×2+1代表着它的区间的后半段。

树状数组

树状数组是一个很奇特的树，它的节点会比线段树少一些，也能表示一个数组。

比如一个数组叫做a有8个数，那么它的树状数组样子就长这样

c数组就是树状数组，能看出来

c1=a1;
c2=a1+a2;
c3=a3;
c4=a1+a2+a3+a4;

以此类推。。。。。。 很难说出他们的关系，但是如果把它们变为二进制

c0001=a0001
c0010=a0001+a0010
c0011=a0011
c0100=a0001+a0010+a0011+a0100

你会发现，将每一个二进制，去掉所有高位1，只留下最低位的1，然后从那个数一直加到1，看一看是不是这样。

线段树构造

因为树状数组不需要构造这一过程，所以先讲线段树的构造

就是用到递归：先设left=1,right=n，然后每一次递归，left、mid和mid+1、right。代码如下：

void build(int left,int right,int index)
    {
        tree[index].left=left;
        tree[index].right=right;
           if(left==right)
            return ;
        int mid=(right+left)/2;
        build(left,mid,index*2);
        build(mid+1,right,index*2+1);
    }

``

线段树单点修改

单点修改就是每到一个节点，看这个节点代表着的区间包括不包括这个点，包括就加上。

void my_plus(int index,int dis,int k)
    {
        tree[index].num+=k;
        if(tree[index].left==tree[index].right)
            return ;
        if(dis<=tree[index*2].right)
            my_plus(index*2,dis,k);
        if(dis>=tree[index*2+1].left)
            my_plus(index*2+1,dis,k);
    }

树状数组单点修改

这里有一个很关键的东西，叫做lowbit，lowbit是将一个二进制数的所有高位一都去掉，只留下最低位的1，比如lowbit（5）=lowbit（0101（二进制））=0001（二进制）

而如果改变x的值，就要加上自己的lowbit，一直加到n，这些节点都要加，比如一共有8个数第3个数要加上k，那么c[0011]+=k;

c[0011+0001] (c[0100])+=k;

c[0100+0100] (c[1000])+=k;

这样就能维护树状数组

void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }

线段树区间查询

区间查询就是，每查到一个区间，有三种选择：

1、如果这个区间被完全包括在目标区间内，那么加上这个区间的和，然后return；

2、如果这个区间的right>目标区间的left，那么查询这个区间；

3、如果这个区间的left<目标区间的right，也查询这个区间;

void search(int index,int l,int r)
    {
        if(tree[index].left>=l && tree[index].right<=r)
        {
            ans+=tree[index].num;
            return ;
        }
        if(tree[index*2].right>=l)
            search(index*2,l,r);
        if(tree[index*2+1].left<=r)
            search(index*2+1,l,r);
    }

树状数组区间查询

就是前缀和，比如查询x到y区间的和，那么就将从1到y的和-从1到x的和。

从1到y的和求法是，将y转为2进制，然后一直减去lowbit(y)，一直到0

比如求1到7的和

ans+=c[0111];
ans+=c[0111-0001(0110)];
ans+=c[0110-0010(0100)];
ans+=c[0100-0100(c[0]无意义，结束)]
    int sum(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }

线段树区间修改

和线段树区间查询类似，分为三种

1、如果当前区间完全属于要加的区间，那么这个区间，也就是节点加上，然后return；

2、如果这个区间的right>目标区间的left，那么查询这个区间；

3、如果这个区间的left<目标区间的right，也查询这个区间;

void pls(int index,int l,int r,int k)
    {
        if(tree[index].left>=l && tree[index].right<=r)
        {
            tree[index].num+=k;
            return ;
        }
        if(tree[index*2].right>=l)
           pls(index*2,l,r,k);
        if(tree[index*2+1].left<=r)
           pls(index*2+1,l,r,k);
    }

树状数组区间修改

这就会变的很好玩。如果将x到y区间加上一个k，那就是从x到n都加上一个k，再从y+1到n加上一个-k

加的移动还是i+=lowbit(i);

void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }

线段树单点查询

就是从根节点，一直搜索到目标节点，然后一路上都加上就好了。

void search(int index,int dis)
    {
        ans+=tree[index].num;
        if(tree[index].left==tree[index].right)
            return ;
        if(dis<=tree[index*2].right)
            search(index*2,dis);
        if(dis>=tree[index*2+1].left)
            search(index*2+1,dis);
    }

树状数组单点查询

从x点，一直x-=lowbit(x)，沿途都加上就好啦

int search(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }

下面给大家分别发一下落谷树状数组1、2的AC代码 （线段树和树状数组都可以做这些题）

树状数组1

线段树代码：

#include <iostream>
    #include <algorithm>
    #include <cstdio>
    #include <cstring>
    #include <cmath>
    #include <queue>
    using namespace std;
    int n,m;
    int ans;
    int he=0;
    int input[500010];
    struct node
    {
        int left,right;
        int num;
    }tree[2000010];
    void build(int left,int right,int index)
    {
        he++;
        tree[index].left=left;
        tree[index].right=right;
           if(left==right)
            return ;
        int mid=(right+left)/2;
        build(left,mid,index*2);
        build(mid+1,right,index*2+1);
    }
    int add(int index)
    {
        if(tree[index].left==tree[index].right)
        {
            //cout<<index<<" "<<input[tree[index].right]<<endl;
            tree[index].num=input[tree[index].right];
            return tree[index].num;
        }
        tree[index].num=add(index*2)+add(index*2+1);
        return tree[index].num;
    }
    void my_plus(int index,int dis,int k)
    {
        tree[index].num+=k;
        if(tree[index].left==tree[index].right)
            return ;
        if(dis<=tree[index*2].right)
            my_plus(index*2,dis,k);
        if(dis>=tree[index*2+1].left)
            my_plus(index*2+1,dis,k);
    }
    void search(int index,int l,int r)
    {
        //cout<<index<<" ";
        if(tree[index].left>=l && tree[index].right<=r)
        {
            ans+=tree[index].num;
            return ;
        }
        if(tree[index*2].right>=l)
            search(index*2,l,r);
        if(tree[index*2+1].left<=r)
            search(index*2+1,l,r);
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            scanf("%d",&input[i]);
        build(1,n,1);
        add(1);
        for(int i=1;i<=m;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(a==1)
            {
                my_plus(1,b,c);
            }
            if(a==2)
            {
                ans=0;
                search(1,b,c);
                printf("%d
",ans);
            }
        }
    }

树状数组代码：

#include <iostream>
    #include <cstdio>
    #include <algorithm>
    #include <cmath>
    #include <cstring>
    using namespace std;
    int n,m,tree[2000010];
    int lowbit(int k)
    {
        return k & -k;
    }
    void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }
    int sum(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        {
            int a;
            scanf("%d",&a);
            add(i,a);
        }
        for(int i=1;i<=m;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            if(a==1)
                add(b,c);
            if(a==2)
                cout<<sum(c)-sum(b-1)<<endl;
        }
    }

树状数组2

线段树代码：

#include <iostream>
    #include <algorithm>
    #include <cstdio>
    #include <cstring>
    #include <cmath>
    #include <queue>
    using namespace std;
    int n,m;
    int ans;
    int input[500010];
    struct node
    {
        int left,right;
        int num;
    }tree[2000010];
    void build(int left,int right,int index)
    {
        tree[index].num=0;
        tree[index].left=left;
        tree[index].right=right;
           if(left==right)
            return ;
        int mid=(right+left)/2;
        build(left,mid,index*2);
        build(mid+1,right,index*2+1);
    }
    /*int add(int index)
    {
        if(tree[index].left==tree[index].right)
        {
            tree[index].num=input[tree[index].right];
            return tree[index].num;
        }
        tree[index].num=add(index*2)+add(index*2+1);
        return tree[index].num;
    }
*/

    void pls(int index,int l,int r,int k)
    {
        if(tree[index].left>=l && tree[index].right<=r)
        {
            tree[index].num+=k;
            return ;
        }
        if(tree[index*2].right>=l)
           pls(index*2,l,r,k);
        if(tree[index*2+1].left<=r)
           pls(index*2+1,l,r,k);
    }
    void search(int index,int dis)
    {
        ans+=tree[index].num;
        if(tree[index].left==tree[index].right)
            return ;
        if(dis<=tree[index*2].right)
            search(index*2,dis);
        if(dis>=tree[index*2+1].left)
            search(index*2+1,dis);
    }
    int main()
    {
        int n,m;
        cin>>n>>m;
        build(1,n,1);
        for(int i=1;i<=n;i++)
            scanf("%d",&input[i]);
        for(int i=1;i<=m;i++)
        {
            int a;
            scanf("%d",&a);
            if(a==1)
            {
                int x,y,z;
                scanf("%d%d%d",&x,&y,&z);
                pls(1,x,y,z);
            }
            if(a==2)
            {
                ans=0;
                int x;
                scanf("%d",&x);
                search(1,x);
                printf("%d
",ans+input[x]);
            }
        }
    }

树状数组代码：

#include <iostream>
    #include <algorithm>
    #include <cstdio>
    #include <cstring>
    #include <cmath>
    #include <queue>
    using namespace std;
    int n,m;
    int input[500010];
    int tree[500100];
    int lowbit(int x)
    {
        return x & -x;
    }
    void add(int x,int k)
    {
        while(x<=n)
        {
            tree[x]+=k;
            x+=lowbit(x);
        }
    }
    int search(int x)
    {
        int ans=0;
        while(x!=0)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }
    int main()
    {
        cin>>n>>m;
        for(int i=1;i<=n;i++)
            cin>>input[i];
        for(int i=1;i<=m;i++)
        {
            int a;
            scanf("%d",&a);
            if(a==1)
            {
                int x,y,z;
                scanf("%d%d%d",&x,&y,&z);
                add(x,z);
                add(y+1,-z);
            }
            if(a==2)
            {
                int x;
                scanf("%d",&x);
                printf("%d
",input[x]+search(x));
            }
        }
    }

总结

最后，再来总结一下

时间复杂度

虽然它们都是nlogn，但是，你会发现，在查询时，树状数组最坏情况是logn（比如8个数，然后查询8），但是线段树是所有情况都是nlogn，稍慢于树状数组。

空间复杂度

树状数组完胜于线段树，线段树要开2倍到4倍内存（推荐4倍），但是树状数组一倍就够了。

适用范围

线段树之所以存在的理由是因为它能适用于很多方面，不仅仅是区间、单点的查询修改，还有标记等等，可以用于模拟、DP等等，而且空间经过离散化以后也可以相对压缩，所以适用范围线段树更加广一些。